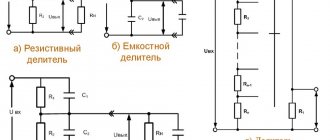
Ток конденсатора при коротком замыкании

Плоский конденсатор

Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).

Как правильно рассчитать ёмкость конденсатора?

Самый простой пример конденсатора – плоская модель. Она имеет форму двух параллельных крышек из проводника, между которыми находится слой диэлектрика. Для того, чтобы знать, как посчитать ёмкость конденсаторов, необходимо применить следующую формулу:

Вам это будет интересно Переход с 380 на 220 вольт

С = e x e0 x s / d,

где S – площадь поверхности пластинок и d – расстояние между ними. В свою очередь, это относительная электрическая проницаемость данного диэлектрика.

Как правило, конденсаторы применяются не по отдельности, а подключаются в более крупные системы. Они могут быть соединены последовательно, параллельно или смешанным способом.

Формула ёмкости

Важно! В последовательно соединённых элементах абсолютное значение заряда на каждой пластине идентично.

Таким образом, результирующее напряжение равно сумме данных показателей на отдельных компонентах прибора.

Общая ёмкость системы будет определяться по формуле:

1/С = 1/С1 + 1/С2 + 1/С3 + …

При параллельном подключении разность потенциалов на каждом из деталей одинакова. Таким образом, суммарный заряд будет равен сумме зарядов на компонентах конденсатора, а результирующая ёмкость – сумме отдельных единичных величин:

C = c1 + c2 + c3 + …

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.

Характеристики конденсаторов

Использование гидропломбы для колодцев

Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.

Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости

Емкость

Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.

В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.

Заряд конденсатора. Напряжение

В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.

На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.

Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.

Формула для нахождения тока конденсатора во время переходного периода:

Ic — ток конденсатора

C — Емкость конденсатора

ΔVc/Δt – Изменение напряжения на конденсаторе за отрезок времени

Зарядка конденсатора

Автор
Сообщение

Зарядка конденсатора

Работа фотовспышки обычно начинается с заряда накопительного конденсатора. Простейший случай – это заряд конденсатора от источника ЭДС через резистор, ограничивающий максимальный ток в цепи:

Заряд конденсатора протекает по экспоненциальному закону. Это можно увидеть по приведенному ниже графику, где по оси X отложено время, измеряемое в RC, а по оси Y — напряжение на конденсаторе в процентах от напряжения источника ЭДС:

Произведение RC называют постоянной времени цепи. Если сопротивление резистора R измерять в килоомах (кОм), а ёмкость конденсатора C — в микрофарадах (мкФ), то произведение RC получится в миллисекундах (мс).

За время t = RC конденсатор успевает зарядится до напряжения, которое составляет 63% от напряжения источника ЭДС, за время t = 3RC – конденсатор зарядится до 95% и при t = 5RC – до 99%. Т.е. при выполнении условия t >> RC напряжение на конденсаторе практически достигнет значения ЭДС.

Очевидно, что чем меньше сопротивление ограничительного резистора и меньше ёмкость конденсатора, тем быстрей этот конденсатор заряжается.

1.1 Заряд конденсатора в кулонах считается по формуле q=CU:

(к, кулон), где С — ёмкость конденсатора, Фарад; U — напряжение на обкладках конденсатора, Вольт.

1.2 Связь зарядного тока, заряда и времени I=q/t, I=CU/t:

(А, ампер), где q — заряд конденсатора, кулоны; t — время, в течение которого переносится заряд, секунды.

1.3 Энергию E в джоулях (ватт*сек) заряженного конденсатора можно рассчитать по формуле E=0,5CU 2 :

(Дж, джоуль), где С — ёмкость конденсатора, Фарад; U — напряжение на обкладках конденсатора, Вольт.

Примечание: иногда удобнее считать, выразив ёмкость в микрофарадах (мкФ), а напряжение в киловольтах (кВ).

Как видно из формулы, зависимость энергии от ёмкости конденсатора линейная, а от напряжения — квадратичная. Т.е. при увеличении напряжения на конденсаторе, например, в два раза энергия, накопленная в нем, возрастет в четыре раза.

1.4 С учетом того, что в импульсной лампе прекращается горение при некотором напряжении, примерно равном 40-70 Вольт в зависимости от типа лампы и её состояния, формула энергии импульса имеет вид разности энергий конденсатора в начале и в конце разряда:

(Дж), где С — ёмкость конденсатора, мкФ; Uн — напряжение на обкладках конденсатора начальное, килоВольт, Uк — напряжение на обкладках конденсатора конечное, килоВольт.

Интересно заметить, что количество теплоты, выделяющейся на резисторе при заряде конденсатора, не зависит от сопротивления этого резистора и равно энергии переданной конденсатору. То есть, половина энергии источника переходит в энергию электрического поля конденсатора, а вторая половина — в тепловую энергию, выделяющуюся в зарядной цепи в виде тепловых потерь.

Re: Зарядка конденсатора

Аналогично происходит зарядка накопительного конденсатора через балластный резистор от источника переменного напряжения, например, от электросети 220 В:

Диод пропускает положительные полуволны напряжения источника, и они распределяются в делителе, образованном резистором R1 и конденсатором C1. По мере роста небольшими «ступеньками» напряжения на конденсаторе C1, амплитуда импульсов на резисторе R1 убывает:

Часто вместо активного сопротивления гасящего резистора используют ёмкостное сопротивление конденсатора. Как известно, конденсатор, установленный в цепи переменного тока, обладает реактивным сопротивлением, зависящим от частоты. Величину ёмкостного сопротивления конденсатора можно определить по формуле:

или с помощью программы Color and Code:

Реактивное сопротивление конденсатора, так же как и сопротивление резистора, может гасить излишнее переменное напряжение сети, причем активная мощность на реактивном сопротивлении конденсатора не выделяется, что является большим преимуществом конденсатора перед гасящим резистором.

Для получения малого реактивного сопротивления необходимо применение конденсаторов большой ёмкости. Поэтому в качестве балластного сопротивления на переменном токе часто используются электролитические конденсаторы. Чтобы полярные конденсаторы могли работать в цепи переменного тока, их включают по следующей схеме:

Диоды на этой схеме создают смещение напряжения, необходимое для нормальной работы конденсаторов. Общая ёмкость такой цепи равна ёмкости последовательно соединенных конденсаторов C1 и C2:

C = (C1 • C2) / (C1+C2)

При равных ёмкостях C1 = C2 — это будет половина ёмкости одного из конденсаторов:

Формула для 3 разных последовательных конденсаторов выглядит так:

С=С1 • C2 • С3/(С2 • C3 + C1 • C3 + C1 • С2)

Следствие из формул: если С1=С2, то С=(С1)/2 — для двух и С=(С1)/3 — для трёх одинаковых конденсаторов.

Re: Зарядка конденсатора

Админ, расскажите еще про быструю зарядку, когда резистор шунтирован транзистором, и по мере его открытия общее балластное сопротивление меняется от R до 0. При этом время заряда получается 100% за RC, то есть в 3-5 раз быстрее.

Хочу простейшую принципиальную схему с минимумом необходимых элементов.

Re: Зарядка конденсатора

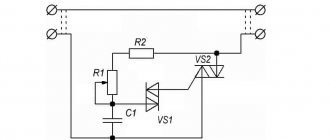
Поскольку из профи про быструю зарядку и шунтирование резистора транзистором никто не написал, мне пришлось изобретать велосипед в Микрокапе. Заряжает на RC на 100% ровно -)). Конечно, тут возможно множество вариантов подключений стабилизирующих элементов, как и множество ошибок -)

Re: Зарядка конденсатора

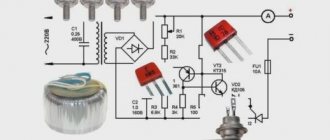
Это схема Осипоффа зарядки ИФК-120 за 0.5 сек

Re: Зарядка конденсатора

Эта схема не то, что Вы рисовали выше. В этой схеме транзистор стоит последовательно с резистором, а у Вас — параллельно.

Эта схема является прерывателем заряда вспышки на время, пока происходит разряд конденсаторов на лампу. Её, пожалуй, надо вот сюда: viewtopic.php?f=26&t=101 и автор, если не ошибаюсь, Waldemar Szymanski. Очень похоже на его стиль рисования схем.

Re: Зарядка конденсатора

Параллельный транзистор взялся из книги Маршака «Импульсные источники света» 1978 г. стр. 352. Компилированная цитата: «Обеспечивающее неизменный зарядный ток переменное сопротивление, которое меняется от Rмакс до нуля, может состоять из резистора Rмакс, параллельно которому в качестве балласта подсоединен транзистор»

Вот я и попытался построить теоретическую схему такого включения. Для практики очевидно следует строить источник стабилизированного тока не с положительной обратной связью, а с отрицательной обратной связью. Простейший вариант видимо такой:

Re: Зарядка конденсатора

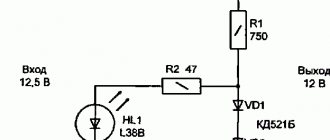
От длительного хранения свойства диэлектрика конденсатора ухудшились и он сейчас пропускает относительно большой ток. Иногда помогает «тренировка конденсатора». Подключите вспышку к источнику переменного напряжения 20-30 Вольт и продержите так, под напряжением, несколько дней. Есть вероятность, что электролит конденсатора восстановится. Можно еще тренировать, формовать залежавшиеся конденсаторы кратковременными подключениями напряжения: включили на 3-5 секунд, сделали паузу на 1-2 часа. И так многократно до восстановления ёмкости конденсатора и уменьшения тока утечки до нормы — для К50-17 не более 1-3 мА.

Мощность, рассеиваемая на резисторе, вычисляется по формуле Джоуля-Ленца: P=I 2 R=I*I*R (Ватт), — где I- среднее значение тока, протекающего по резистору (Ампер), R — величина сопротивления (Ом).

Re: Зарядка конденсатора

Так не считают. А если резистор поставить ДО диода, то на нём будет 220 В?

В схеме вашей вспышки резистор, диод и конденсатор образуют последовательную цепочку, подключенную к переменному напряжению 220 В. Следовательно, во время заряда вспышки будет протекать пульсирующий ток, одинаковый для всех элементов последовательной цепи. Величина тока определяется суммарным сопротивлением цепи и разницей между амплитудным напряжением сети и действующим значением напряжения на конденсаторе. Чем больше конденсатор заряжается, тем меньше эта разница и тем меньше зарядный ток. Для расчета мощности резистора приходится считать средний ток за то время, пока конденсатор набирает энергию. Также, зная время заряда, ёмкость и напряжение конденсатора, можно получить величину среднего тока из формулы переноса заряда

Разряд конденсатора

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу τ (тау). За один τ конденсатор заряжается или разряжается на 63%. За пять τ конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Основные формулы ёмкости

Базовый расчёт конденсатора предполагает выявление зависимости емкости и заряда, удерживаемого на элементе, а также напряжением на пластинах.

C=QVC=QV

C – емкость, или объём в Фарадах Q – заряд, удерживаемый на пластинах в кулонах V – разность потенциалов между пластинами в вольтах

Это уравнение используется для расчета работы, необходимой для зарядки конденсатора и энергии, хранящейся в нем.

Формула энергии

W=∫Q0V dQW=∫0QV dQ

W=∫Q0qC dQW=∫0QqC dQ

W=12CV2

Важно! Необходимо знать, какое влияние конденсатор будет оказывать на любую цепь, в которой он работает. Он не только предотвращает прохождение постоянной составляющей тока сигнала, но и оказывает влияние на любой переменный сигнал.

Реактивное сопротивление

В цепи постоянного тока помимо батареи может присутствовать резистор, который оказывает сопротивление току в цепи. То же справедливо и для схемы переменного тока с элементом, накапливающим заряд. Конденсатор с небольшой площадью пластины позволяет хранить только небольшое количество заряда, и это будет препятствовать протеканию тока. Конденсатор имеет определенное реактивное сопротивление, и оно зависит от его величины, а также от частоты срабатывания. Чем выше частота, тем меньше реактивное сопротивление.

Вам это будет интересно Соединение резисторов

Фактическое реактивное сопротивление можно вычислить по формуле:

Xc = 1 / (2 pi f C)

где

Xc – ёмкостное реактивное сопротивление в Омах. f – частота в Герцах. C – ёмкость в Фарадах.

Текущий расчет

Реактивное сопротивление конденсатора, рассчитанное по приведенной выше формуле, измеряется в Омах. Затем ток, протекающий в цепи, может быть рассчитан обычным способом с использованием закона Ома:

V = I Xc

Главный показатель конденсатора

Расстояние между пластинами

Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).

Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость ɛ. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

Воздух – 1.0005

Бумага – от 2.5 до 3.5

Стекло – от 3 до 10

Слюда – от 5 до 7

Порошки оксидов металлов – от 6 до 20

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора

устремятся к положительному полюсу источника, в связи с чем на обкладке возникнет недостаток отрицательно заряженных частиц и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора, в результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную . Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока, после этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать
ток разряда конденсатора
, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Источник

Номинальное напряжение

Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).

Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.