Расчет мощности трехфазной сети
Количество потребленной энергии в сети однофазного тока определяется простейшими расчетами, это не вызывает затруднений. Расчет мощности трехфазной сети сопряжен с некоторыми трудностями:
- Наличие трех фаз вместо одной;
- Различные схемы соединения потребителей – «звезда» или «треугольник»;
- Симметрия или ее отсутствие при распределении нагрузки по фазам.
Мощность трехфазной сети: активная, реактивная, полная
Значения общей активной и общей реактивной мощностей трехфазной цепи равны соответственно суммам активных и реактивных мощностей для каждой из трех фаз A, B и C. Это утверждение иллюстрируют следующие формулы:
здесь Ua, Ub, Uc, Ia, Ib, Ic – значения фазных напряжений и токов, а φ — сдвиг фаз.
Когда нагрузка является симметричной, то есть в условиях когда активные и реактивные мощности каждой из фаз равны между собой, для нахождения общей мощности многофазной цепи достаточно умножить значение фазной мощности на количество задействованных фаз. Полная мощность определяется исходя из полученных значений активной и реактивной ее составляющих:
В приведенных формулах можно выразить фазные значения величин через линейные их значения, которые для схем соединения потребителей звездой или треугольником будут отличаться, однако формулы для мощности в итоге окажутся одинаковыми:
Из приведенных выражений следует, что вне зависимости от схемы соединения приемников электрической энергии, треугольник ли это или звезда, если нагрузка симметрична, то формулы для нахождения мощности будут иметь одинаковый вид, как для треугольника, так и для звезды:
В данных формулах указаны линейные значения величин напряжения и тока, и они записаны без индексов. Именно такая запись, без индексов, встречается обычно, то есть если нет индексов, то имеются ввиду линейные значения.
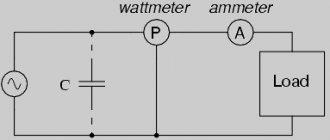
Для проведения измерений применительно к активной мощности в электрической цепи, используют специальный измерительный прибор, который называется ваттметром. Его показания определяются в соответствии с формулой:
в приведенной формуле Uw и Iw – векторы приложенного к нагрузке напряжения и протекающего через нее тока.
Характер активной нагрузки и схема соединения фаз могут быть разными, поэтому в зависимости от конкретных обстоятельств и схемы включения ваттметров будут различными.
Для симметрично нагруженных трехфазных цепей, с целью ориентировочного измерения общей активной мощности, если не требуется высокая точность, достаточно одного ваттметра, включенного лишь в одну из фаз. Затем, для получения значения активной мощности полной цепи, остается умножить показания ваттметра на количество фаз:
Для четырехпроводной цепи с нулевым проводом, чтобы точно измерить активную мощность, необходимы три ваттметра, с каждого из которых снимаются показания, и затем суммируются для получения значения общей мощности цепи:
Если нулевой провод в трехфазной цепи отсутствует, то для измерения общей мощности достаточно двух ваттметров, даже если нагрузка несимметрична.
В отсутствие нулевого провода, токи фаз связаны друг с другом в соответствии с первым законом Кирхгофа:
Тогда сумма показаний пары ваттметров будет равна:
Так, если сложить показания пары ваттметров, то получится общая активная мощность в исследуемой трехфазной цепи, причем показания ваттметров будут зависеть как от величины нагрузки, так и от ее характера.
Взглянув на векторную диаграмму токов и напряжений применительно к симметричной нагрузке, можно придти к выводу, что показания ваттметров определяются по следующим формулам:
Проанализировав эти выражения, можно понять, что при чисто активной нагрузке, когда φ = 0, показания двух ваттметров окажутся равны между собой, то есть W1 = W2.
При активно-индуктивном характере нагрузки, когда 0 ≤ φ ≤ 90°, показания ваттметра 1 окажутся меньше чем у ваттметра 2, то есть W1 60° показания ваттметра 1 будут отрицательными, то есть W1
При активно-емкостном характере нагрузки, когда 0 ≥ φ≥ -90°, показания ваттметра 2 будут меньше чем ваттметра 1, то есть W1 > W2. При φ
Источник
Как узнать свою схему
Для правильного определения и расчета мощности требуется знание нескольких факторов:
- Количества фаз питания;
- Способа соединения потребителей.
При однофазном подключении используется два провода:
- Фазный провод;
- Нулевой провод.
Для трехфазной сети характерно наличие трех или четырех проводников (подключение с заземленной нейтралью). При этом используется две различных схемы включения:
- «Треугольник». Каждая нагрузка подсоединяется с двумя соседними. Напряжение каждой фазы подводится к точкам соединения потребителей.
- «Звезда». Все три потребителя соединяются в одной точке. Ко вторым концам подключаются фазы питания. Это схема с изолированной нейтралью. В схеме с заземленной нейтралью точка соединения потребителей подключается к нулевому проводнику.
Трёхфазное или однофазное подключение
В зависимости от того, какой тип подключения используют, определение потребляемой мощности производится по-разному.
В однофазной сети потребляемая энергия считается по простейшей формуле:
где cosϕ – коэффициент мощности, характеризующий сдвиг фаз между током и напряжением в реактивной нагрузке.
Мощность 3 х фазной сети является суммой потребления по каждой фазе в отдельности. Формула мощности 3 х фазного тока имеет следующий вид:
Pобщ=Uа∙Iа∙cosϕа+ Ub∙Ib∙cosϕb+ Uc∙Ic∙cosϕc,
где U, I, cosϕ – напряжение, сила тока и коэффициент мощности в каждой фазе, соответственно.
К сведению. Видно, что в общем случае трехфазное соединение требует большее количество приборов учета.
Иногда посчитать потребление энергии можно по упрощенному варианту. При симметричном потреблении, например, при подключении асинхронного двигателя, токи потребления одинаковы, и формула принимает следующий вид:
где:
- Uф, Iф – фазные напряжение и ток;
- Uл, Iл – линейные напряжение и ток.
Соединение потребителей звездой
В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз P = Pa + Pb + Pc, где Pa = Ua Ia cos φa; Pb = Ub Ib cos φb; Pc = Uc Ic cos φc; Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и токи; φa, φb, φc – углы сдвига фаз между напряжением и током.
Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз Q = Qa + Qb + Qc, где Qa = Ua Ia sin φa; Qb = Ub Ib sin φb; Qc = Uc Ic sin φc.
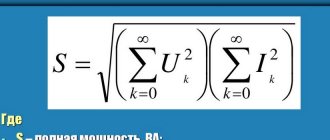
Полная мощность отдельных фаз Sa = Ua Ia; Sb = Ub Ib; Sc = Uc Ic. Полная мощность трехфазного приемника .
При симметричной системе напряжений (Ua = Ub = Uc = UФ) и симметричной нагрузке (Ia = Ib = Ic = IФ; φa = φb = φc = φ) фазные мощности равны Pa = Pb = Pc = PФ = UФ IФ cos φ; Qa = Qb = Qc = QФ = UФ IФ sin φ.
Активная мощность симметричного трехфазного приемника
P = 3 PФ = 3 UФ IФ cos φ.
Аналогично выражается и реактивная мощность
Q = 3 QФ = 3 UФ IФ sin φ.
Полная мощность
S = 3 SФ = 3 UФ IФ.
Отсюда следует, что в трехфазной цепи при симметричной системе напряжений и симметричной нагрузке достаточно измерить мощность одной фазы и утроить результат.
Характеристики трехфазной системы
Трехфазная система электропитания характеризуется несколькими значениями напряжения и тока. Все зависит от того, между какими точками схемы производятся измерения:
- между фазным проводом и нейтралью – фазное напряжение Uф;
- между отдельными фазами – линейное Uл.
Соотношение между данными параметрами:
При симметричном распределении нагрузки токи во всех проводах равны. В четырехпроводной схеме (с заземленным нулем) ток в нулевом проводнике отсутствует, поэтому даже при обрыве нуля сеть продолжает нормально функционировать.
В том случае, когда потребление энергии по фазам различается, в нейтральном проводе протекает некоторый ток. Полный обрыв нейтрального проводника вызывает перекос фаз, поэтому напряжение на проводах может измениться в диапазоне от нуля до линейного.
Пример расчёта мощностных показателей
Наиболее простым примером может считаться расчет потребления энергии симметричной нагрузкой. Сколько будет потреблять электроэнергии трехфазный асинхронный двигатель, подключенный в сеть с линейным напряжением 380 В, и потребляющий ток 10 А по каждой фазе? Коэффициент мощности cosϕ=0.76. Тогда потребляемая мощность равна:
Более сложный расчет бытовой сети:
- Фазное напряжение – 220 В;
- Потребление по линиям – 10 А, 5 А, 2 А;
- Первые две фазы подключены к активной нагрузке (электроплита, чайник);
- Третья нагружена на люминесцентные светильники с cosϕ=0,5.
Pобщ=Uа∙Iа∙cosϕа+ Ub∙Ib∙cosϕb+ Uc∙Ic∙cosϕc=220∙10+220∙5+220∙2∙0,5=3520 ВА.
Используя онлайн калькулятор расчетов, можно избавиться от большинства ошибок и сократить время вычислений. Требуется лишь правильно ввести данные по текущим параметрам
Формула расчета мощности электрического тока
Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.
В реальных условиях в формулу добавляется еще одна составляющая и формула для однофазной сети приобретает вид:
I = P/(U*cos φ),
а для трехфазной сети: I = P/(1,73*U*cos φ),
где U для трехфазной сети принимается 380 В, cos φ – это коэффициент мощности, отражающий соотношение активной и реактивной составляющих сопротивления нагрузки.
Виды клемм для соединения проводов: советы по выбору
Схема подключения УЗО: инструкция, методы, ошибки
Для современных блоков питания реактивная компонента незначительна, величину cos φ можно принимать равной 0,95. Исключение составляют мощные трансформаторы (например, сварочные аппараты) и электродвигатели, они имеют большое индуктивное сопротивление. В сетях, где планируется подключение подобных устройств, максимальную силу тока следует рассчитывать с использованием коэффициента cos φ, равного 0,8 или рассчитать силу тока по стандартной методике, а потом применить повышающий коэффициент 0,95/0,8 = 1,19.
Подставив действующие значения напряжения 220 В/380 В и коэффициента мощности 0,95, получаем I = P/209 для однофазной сети и I = P/624 для трехфазной сети, то есть в трехфазной сети при одинаковой нагрузке ток втрое меньше. Никакого парадокса тут нет, так как трехфазная проводка предусматривает три фазных провода, и при равномерной нагрузке на каждую из фаз она делится натрое. Поскольку напряжение между каждым фазным и рабочим нулевым проводами равно 220 В, можно и формулу переписать в другом виде, так она нагляднее: I = P/(3*220*cos φ).
Что такое УЗО в электрике: разновидности, принцип работы
Подключение двухклавишного выключателя: схемы, советы, инструкция
Измерение мощности ваттметром
Мощность потребления трехфазного тока измеряют, используя ваттметры. Это может быть специальный ваттметр, для 3-х фазной сети, либо однофазный, включенный по определенной схеме. Современные приборы учета электроэнергии часто выполняются по цифровой схемотехнике. Такие конструкции отличаются высокой точностью измерений, большими возможностями оперирования с входными и выходными данными.
Варианты измерений:
- Соединение «звезда» с нулевым проводником и симметричная нагрузка – измерительный прибор подключается к одной из линий, считанные показания умножаются на три.
- Несимметричное потребление тока в соединении «звезда» – три ваттметра в цепи каждой фазы. Показания ваттметров суммируются;
- Любая нагрузка и соединение «треугольник» – два ваттметра, подключенных в цепь любых двух нагрузок. Показания ваттметров также суммируются.
На практике всегда стараются выполнить нагрузку симметричной. Это, во-первых, улучшает параметры сети, во-вторых, упрощает учет электрической энергии.
Мощность трехфазной цепи
2015-02-27 16577
Активная мощность трехфазной цепи равна сумме активных мощностей потребляемых каждой фазой нагрузки:
При симметричной нагрузке мощности, потребляемые каждой фазой нагрузки равны. В этом случае , а мощность, потребляемая каждой фазой, определяется как: .
где j — угол сдвига между фазным напряжением и током.
Рисунок 4.11 — Векторная диаграмма для несимметричной нагрузки, соединенной треугольником
Реактивная мощность трехфазной цепи равна сумме реактивных мощностей отдельных фаз:
При симметричной нагрузке реактивные мощности отдельных фаз равны и реактивная мощность трехфазной цепи , реактивная мощность одной фазы: .
Мощность трехфазной цепи при несимметричной нагрузке
ЛЕКЦИЯ 9
Трехпроводная цепь(продолжение)
Соединение фаз приемника треугольником
Один из основных способов заметного изменения мощности при отключенной нагрузке – переключение схемы соединения источника и приемника со звезды на треугольник и наоборот.
При включении начала одной фазы с концом другой с образованием замкнутого контура получают соединение треугольником.
Соединяют треугольником фазы приемника, т.е. три фазы приемника включены между линейными проводами рис 1.
Фазные напряжения приемника равны соответствующим линейным напряжениям источника питания:
т.е.
фазные токи:
Положительное направление фазных напряжений
, и совпадает с положительным направлением фазных токов.
При соединении треугольником приемника получается замкнутый контур, поэтому:
Фазные напряжения определяются как линейные генератора:
; ;
Определение фазных и линейных токов
Токи в фазах определяются по закону Ома:
.
Линейные токи определяются по фазным токам по первому закону Кирхгофа:
Линейные токи равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом.
независимо от характера нагрузки сумма линейных токов всегда равна 0.
При изменении одной из фаз режим работы других фаз остается неизменным, т.к. линейное напряжение генератора остается постоянным. Соединение треугольником используется для несимметричной нагрузки.