Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).
Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
- µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
- l — длина проводника в метрах;
- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Варианты измерения
Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.
Прямой метод
Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.
Порядок проведения измерений включает в себя следующие этапы:
- К прямопоказывающему приспособлению подключают катушку.
- После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
- Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.
Измерительными приборами
Если под руками имеются измерительные приборы, то с их помощью довольно просто найти силу тока. Необходимо лишь соблюдать правила измерений и не забывать о правилах безопасности.
Амперметром
Пользуясь приборами для измерения ампеража, следует помнить, что они подключаются в цепи последовательно. Внутреннее сопротивление амперметра очень маленькое, поэтому прибор легко выводится из строя, если проводить измерения пределами значений, для которых он рассчитан.
Калькулятор расчета многослойной катушки индуктивности
На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить – намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.
Для расчета индуктивности многослойной катушки используется такая формула:
- d – сумма диаметра каркаса и толщины намотки только с одной стороны;
- n – количество витков;
- g – толщина намотанной проволоки;
- h – высота намотанной проволоки;
Из этой формулы, зная величину индуктивности, можно вывести толщину намотки:
Для определения количества витков необходимо воспользоваться формулой:
- dпр – диаметр провода
- h – высота катушки;
- g – толщина намотки.
Расчет количества витков
Длину одного витка можно определить следующим образом:
Где π – это константа, а dвит_— это диаметр витка.
Тогда, зная общее число витков и принимая, что d – это усредненное значение диаметра для всех витков, длина всего провода будет определяться по формуле:
Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.
где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь проводника, которая определяется по формуле:
Подставив значение площади и длины провода, получим такое выражение для определения сопротивления:
Из значения сопротивления можно вывести формулу для определения диаметра провода, подставив предварительно формулу для вычисления количества витков:
После получения величины диаметра провода, можно определить количество витков, которое подставляется с остальными данными в первую формулу для расчета индуктивности.
Число слоев можно определить, разделив толщину намотки на диаметр провода:
Посредством вышеприведенных вычислений можно определить все параметры многослойной катушки индуктивности, которые помогут вам изготовить устройство с нужными параметрами. Также, чтобы облегчить вычисления вы можете воспользоваться нашим онлайн калькулятором ниже.
Поделиться в социальных сетях
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Источник
Комментарии и отзывы (7)
Вадим
Почему во всех каликуляторах расчёта индуктивности нет учитывания магнитной проницаемости разных видов сердечников и без него. Наматывается количество витков не понятно относительно чего, воздуха феррита или железа.
Роман
Длина намотки (имеется ввиду) — длина каркаса катушки
Валерий
использовал этот калькулятор для расчёта 0,5 мГн проводом 1 мм на каркасе диаметром 23 мм длиной 30 мм намотка внавал … калькулятор выдал 178 витков,намотал 180, реальная измеренная индуктивность 550 мкГн
Расчет катушки индуктивности
Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла. Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.
Смотрите также
Очень странный результат получается. На 3,4 мГ d20 L35 провод 1/1,2 получается один слой и расход провода менее одного метра. Как это??
Попробуйте поменять микрогенри на милигенри
Может попутали милигенри и микрогенри?
Тут расчет явно без сердечника, иначе были бы другие данные, например проницаемость сердечника.
А как же сердечник? С сердечником или без него?
Ингвар, да чтож вам так нужны букввы НННН? Длина! Дарю.
Длинна намотки это длинна катушки от точки начала намотки до конча рассчитанного проводника(метры), длинна проводника рассчитывается из нужного вам сопротивления. Например для магнитной системы вам надо не менее 1мм и не более 3 (2слоя намотки), а из-за длинны проводника у вас получается 6мм, придется увеличивать число слоев (до 4х) сделать катушку толще, но короче.
Главное индуктивность и сопртивение. Чем длиннее провод, тем больше его сопротивление!
Длина намотки никак не влияет на результаты. Так и должно быть?
Источник
Идеальные и реальные катушки индуктивности
У идеальных катушек индуктивности при подключении их к источнику синусоидального напряжения ток отстает по фазе от напряжения на p/2, индуктивное сопротивление RL
= w
L
, где
L
–индуктивность (коэффициент самоиндукции). Как и в случае конденсаторов, у реальных катушек фазовый сдвиг между током и напряжением несколько меньше p/2 – на величину
d
, из-за потерь энергии в катушке при протекании по ней переменного тока – в основном за счет нагрева провода обмотки. Величину называют
добротностью катушки
. Для последовательной схемы замещения , для параллельной .
В некоторых случаях, особенно при высоких частотах, применяют более сложные эквивалентные схемы, учитывающие дополнительно индуктивность выводов конденсаторов и межвитковую емкость катушек.
Низкочастотные измерительные мосты переменного тока
Емкости и тангенсы углов диэлектрических потерь конденсаторов, индуктивности и добротности катушек можно измерять при помощи различных мостовых схем. Рассмотрим схему четырехплечего моста:
Рис. 3.
Его плечи могут содержать активные сопротивления, емкости и индуктивности и характеризуются импедансами (комплексными сопротивлениями) . С
хема питается переменным синусоидальным напряжением. Условие баланса моста переменного тока (т.е. равенства нулю тока индикатора И) аналогично условию баланса моста постоянного тока (см. работу №10):
| (5) |
Выбор конкретной схемы моста зависит от того, какой эквивалентной схемой мы хотим представить исследуемый конденсатор или катушку индуктивности. Для последовательной схемы замещения конденсатора удобно применять мост следующего вида:
Рис. 4.
Здесь R0
— градуированный (снабженный шкалой) переменный резистор, C
0
— градуированный конденсатор с минимальными потерями (с воздушным диэлектриком). Условие (5) для этой схемы запишется в виде:
| или | (6) |
Чтобы были равны два комплексных числа, необходимо, чтобы были равны соответственно их действительные и мнимые части. Поэтому равенство (6) распадается на два:
| R X R 2 = R0R 1 и | (7) |
Из этих выражений получаем два условия баланса моста, которые должны выполняться одновременно:
| (8) |
| (9) |
Образцовые катушки индуктивности в мостах переменного тока почти не применяются, т.к. трудно изготовить катушку с очень малыми потерями. Для измерения параметров катушек при последовательной схеме замещения обычно применяют мост следующего вида:
Рис. 5.
Условие (5) для этой схемы запишется в виде:
| (10) |
откуда, после упрощений и разделения действительной и мнимой частей, получаем:
| (11) |
и
| (12) |
Балансировку рассмотренных мостов осуществляют поочередным изменением величин C0
и
R0
. Для расширения пределов измерений иногда ступенчато изменяют величины
R
1/
R
2 или
R
1
R
2.
Расчет катушки индуктивности
При построении электронных устройств часто приходится сталкиваться с индуктивным элементом схемы. Когда на чертеже указано только значение индуктивности L, то расчет катушки индуктивности приходится выполнять самостоятельно. В интернете есть множество программ, позволяющих выполнять расчёт индуктивности катушек онлайн при помощи специального калькулятора. Зная то, как устроен элемент, можно вручную произвести все вычисления.
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Что такое катушка индуктивности
Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.
Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока. При этом нет разницы, увеличивается он или уменьшается.
В связи с этим данные элементы применяют в электротехнике для осуществления:
- токоограничения;
- ослабления биений;
- помехоподавления;
- формирования магнитного поля;
- изготовления датчиков движения.
Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.
Энергия магнитного поля катушки индуктивности
Электрический ток способствует накоплению энергии в магнитном поле катушки. Если отключить подачу электричества, накопленная энергия будет возвращена в электрическую цепь. Значение напряжения при этом в цепи катушки возрастает многократно. Величина запасаемой энергии в магнитном поле равна примерно тому значению работы, которое необходимо получить, чтобы обеспечить появление необходимой силы тока в цепи. Значение энергии, запасаемой катушкой индуктивности можно рассчитать с помощью формулы.
Какие параметры есть у катушки
От того, где будет применяться индуктивный элемент и на какой частоте работать, зависит его исполнение. Имеются общие параметры:
- L – индуктивность;
- R пот – сопротивление потерь;
- Q – добротность;
- свой резонанс и паразитарная ёмкость;
- коэффициенты ТКИ и ТКД.
Индуктивность (коэффициент самоиндукции) L – это главная электрическая характеристика элемента, которая показывает количество накапливаемой дросселем энергии при передвижении тока. Величина энергии в катушки тем выше, чем больше её индуктивность. Единица измерений L – 1 Гн.
Преобразования энергии в катушке индуктивности
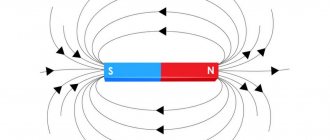
Из курса физики в 11 классе известно, что электрический ток, проходящий через катушку индуктивности, создает магнитное поле. В результате самоиндукции изменение этого магнитного поля наводит в этой же катушке ЭДС индукции, которая, согласно правилу Ленца, направлена так, чтобы противодействовать причине, его вызвавшей.
Рис. 1. Правило Ленца.
Можно сказать, катушка индуктивности «сопротивляется» любым изменениям тока через нее, и электрическому полю необходимо затратить энергию для таких изменений (как для увеличения тока, так и для его уменьшения).
Куда девается эта энергия?
Поскольку никаких «приемников энергии» в катушке индуктивности нет, то можно заключить, что энергия электрического поля тратится на «разгон» электронов в катушке и на создание магнитного поля в ней. Если электрическое поле снять, то электроны также не сразу остановятся, а за счет энергии магнитного поля будут еще некоторое время двигаться, возвращая энергию в проводник.
Таким образом, катушка индуктивности обладает способностью накапливать энергию в магнитном поле. При включении тока его энергия затрачивается на создание магнитного поля, а при выключении — энергия магнитного поля тока возвращается в проводник.
Подчеркнем, что энергия магнитного поля имеет существенно иную природу, чем внутренняя энергия проводника, которая выражается законом Джоуля-Ленца. Энергия магнитного поля тока — это кинетическая энергия зарядов, упорядоченно движущихся по ней. Внутренняя энергия проводника — это энергия хаотического движения молекул самого проводника. Энергию магнитного поля легко получить, уменьшая ток в проводнике. В этом случае магнитное поле катушки, уменьшаясь, будет совершать положительную работу. Получить внутреннюю энергию поля без дополнительных затрат энергии запрещает второе начало термодинамики.
Рис. 2. Второе начало термодинамики.
Конструкция катушки
По конструктивному исполнению индуктивные элементы различаются:
- видом намотки: винтоспиральная, винтовая; кольцевая;
- количеством слоёв: однослойные или многослойные;
- типом изолированного провода: одножильный, многожильный;
- наличием каркаса: каркасные или бескаркасные (при небольшом количестве витков толстого провода);
- геометрией каркаса: прямоугольный, квадратный, тороидальный;
- наличием сердечника: ферритовый, из карбонильного железа, электротехнической стали, пермаллоевый (магнитомягкий сплав), металлический (латунный);
- геометрией сердечника: стержневой (разомкнутый), кольцо-образный или ш-образный (замкнутый);
- возможностью изменять L в узких интервалах (движение сердечника по отношению к обмотке).
Существуют плоские катушки, в печатном исполнении устанавливаемые на платах цифровых устройств.
К сведению. Намотка провода может быть как рядовой (витком к витку), так и в навал. Последний способ укладки провода снижает паразитную ёмкость.
Схема замещения катушки индуктивности малого номинала на — большего.
Казалось бы, какие проблемы могут быть связаны с малыми значениями индуктивностей катушек? Наоборот — витков поменьше, провод потолще… Сиди и радуйся, не умеешь радоваться — просто сиди. А радоваться, действительно, есть чему: это и приемлемые массогабаритные характеристики, и низкие потери, и высокая добротность подобных моточных изделий. Так ведь нет, что-то душеньке радиолюбительской неймётся при встрече с изображениями катушек наногенриевых номиналов. Причём, если с величинами индуктивностей 25 — 35нГн особых проблем не возникает (это 2-3 витка миллиметрового провода, намотанного на 5мм оправке), то номиналы менее 10нГн порой вызывают замешательство и чувство недоумения на лице молодого разработчика. Опытные СВЧисты, конечно, посмеются подобной постановке проблемы, они-то прекрасно знают, что подобные катушки легко и непринуждённо реализуются на полосковых линиях. Однако для нас, простых пацанов, а также недоступных для понимания и логического анализа загадочных девушек, окажется весьма кстати эквивалентная схема замещения катушки малого номинала на изделие, доступное для внятной намотки. Тут ничего изобретать не надо, схема эта известна и приведена на Рис.1. Рис.1
Поскольку в последовательном контуре суммарный сдвиг фаз между напряжениями на катушке и на конденсаторе составляет 180°, то равенство характеристических сопротивлений обеих цепей будет выглядеть следующим образом: XL = XL1 — XC1 ;
Произведя необходимые преобразования, получим формулу для расчёта ёмкости конденсатора С1 для требуемого значения индуктивности L1: C1 = 1/[(2πF)2×(L1 — L)] ;
Сдобрим полученную формулу калькулятором.
РАСЧЁТ ЭЛЕМЕНТОВ ЦЕПИ ЗАМЕЩЕНИЯ КАТУШКИ ИНДУКТИВНОСТИ.
Будда призывал своих учеников не верить никому на слово (даже ему), и, прежде чем принять чьи-то советы, тщательно выяснять, а соответствуют ли они действительности. Поступим так же и мы.
Рис.2
Для начала рассмотрим схему цепи согласования выходного каскада передатчика с антенной (Рис.2). Расчёт элементов был произведён для частоты 145МГц на странице ссылка на страницу. А теперь давайте посмотрим, как поведёт себя коэффициент передачи и АЧХ цепи при замене катушки индуктивности L1 номиналом 7нГн на цепочку, представленную на Рис.1.
Рис.3
На верхней диаграмме Рис.3 приведена АЧХ цепи при изначальной L1=7нГн, ниже — при замене L1 на цепочку, состоящую из: 20нГн и 91пФ, ещё ниже — при замене на цепочку: 40нГн и 36пФ. Ну, что тут скажешь? Налицо незначительное уменьшение коэффициента передачи и значительное сужение полосы пропускания. Причём, чем большее значение принимает новая катушка по отношению к первоначальной, тем сильнее проявляются данные эффекты.
А теперь давайте то же самое проделаем с межкаскадной согласующей цепью, рассчитанной на странице ссылка на страницу.
Рис.4
Рис.5
Катушки индуктивности в данном случае были использованы номиналами 6.5, 20 и 40нГн. Тенденция наблюдается такая же, как и в предыдущем случае, но менее ярко выраженная. Да это и понятно — при столь низком сопротивлении нагрузки добротность нагруженного контура получается значительно ниже.
Какие можно сделать выводы, наблюдая за описанными выше потоками движения электронов в модифицированных катушках? В принципе, подобная схема замещения малых индуктивностей на катушки бОльших номиналов имеет право на жизнь. Несмотря на некоторое ухудшение передаточных характеристик и сужение полосы пропускания согласующих устройств, возможность изготовления моточного изделия с предсказуемыми параметрами может для кого-то явиться решающим фактором при выборе данного схемотехнического решения. Тут важно не сильно усердствовать и не гнаться за значительными величинами, а ограничиться коэффициентом повышения индуктивности — в 3-4 раза.
Расчет параметров катушки
Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.
Расчет L в зависимости от заданной конструкции
Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:
L = 0,01*D*w2/(l/D) + 0,46,
где:
- D – диаметр каркаса, см;
- w – число витков;
- l – длина намотки, см;
- L – индуктивность, мкГн.
Подставляя численные значения в формулу, получают значение L.
Расчет количества витков по индуктивности
Зная D каркаса и L, рассчитывают количество витков в катушке, формула имеет вид:
где:
- L – индуктивность, мкГн;
- D – диаметр каркаса, мм.
Если в качестве исходных параметров берутся длина навитого в ряд проводника и его диаметр, то количество витков находят, используя формулу:
где:
- l – длина намотки, мм;
- d – диаметр провода, мм.
Измерения диаметра провода проводят линейкой или штангенциркулем.
Расчёт индуктивности прямого провода
Собираясь найти L круглого прямого проводника, обращаются к приближённой формуле:
L = (μ0/2π)*l*( μe*ln(l/r) + 1/4* μi,
где:
- μ0 – магнитная постоянная;
- μe – относительная магнитная проницаемость (ОМП) среды (для вакуума – 1);
- μi – ОМП проводника;
- l – длина провода;
- r – радиус провода.
Формула справедлива для длинного проводника.
Расчёт однослойной намотки
Однослойные дроссели без сердечника легко и быстро можно рассчитать при помощи онлайн-калькулятора, в окно которого можно забить все известные характеристики, и программа выдаст значение L.
Вычисления проводятся и вручную, с использованием математического выражения. Оно имеет вид:
L = D2*n2/45D + 100*l,
где:
- D – диаметр катушки, см;
- l – длина намотанного провода, см;
- n – количество витков.
Формула подходит для вычислений L дросселей без ферритовых сердечников.
Дроссель с сердечником
При наличии сердечника следует учесть его размеры и форму. В случае одинаковых катушках индуктивность больше у той, которая располагается на сердечнике.
Многослойная намотка
Особенности расчёта при подобном способе наматывания провода заключаются в том, что нужно учитывать его толщину. Формула для дросселя без сердечника имеет вид:
где:
- Dk – общий диаметр (диаметр каркаса и намотки);
- t – толщина слоя;
- l – длина накрученного провода.
Все значения подставляют в мм, величину L – в мкГн.
Эквивалентная схема реальной катушки индуктивности
Каждый дроссель можно представить в виде эквивалентной схемы.
Данная схема состоит из элементов:
- Rw – сопротивление обмотки с выводами;
- L – индуктивность;
- Cw – паразитная ёмкость;
- Rl – сопротивление потерь.
Изготавливая индуктивный элемент, стремятся снизить величину сопротивления потерь, паразитную ёмкость. При работе катушки на низкой частоте учитывают сопротивление её обмотки Rw. На таких частотах действуют токи большой величины.
Правильно рассчитанная катушка индуктивности будет иметь высокую добротность (180-300) и стабильность работы при влиянии внешних условий (температуры и влажности). Зная способы различной намотки и манипуляции с шагом, можно уменьшить влияние паразитных факторов.
ЭКВИВАЛЕНТНАЯ СХЕМА КАТУШКИ ИНДУКТИВНОСТИ. ПОНЯТИЕ ДОБРОТНОСТИ.
Индуктивность обычно составляет 7-10% от общего числа элементов электронных аппаратов. Индуктивность делят на 2 группы по типу сердечников: — магнитный, -немагнитный(воздушный). Магнитные сердечники: — замкнутые, — разомкнутые. Реальные индуктивности не являются чистыми индуктивностями, т.к. провод на который она навивается обладает последовательным сопротивлением R, а между витками обмотки имеется распределенная межвитковая емкость. Одно из особенностей индуктивности является их чувствительность к паразитным магнитным полям и способность генерировать электрические поля. Источниками помех являются катушки индуктивности с воздушным и разомкнутым магнитным сердечником, поскольку Ф от них выходит за пределы катушки на значительные расстояния. Индуктивность на замкнутом магнитном сердечнике создает намного меньшее магнитное поле рассеяния и почти весь Ф остается внутри магнитного сердечника. Катушки с магнитным сердечником более чувствительны к магнитным полям, чем катушки с воздушным сердечником. При низкой частоте эквивалентная схема катушки индуктивности:
Сопротивление катушки увеличивается с ростом частоты из-за поверхностного эффекта и эффекта близости. Поэтому добротность катушки Q
не пропорциональна её частоте. При высоких частотах нельзя пренебрегать емкостями между витками. Из-за межвитковых емкостей, при высоких частотах эквивалентные и реактивные сопротивления катушки могут стать емкостными.
РЕАЛЬНЫЕ ПРАМЕТРЫ ПРОВОДНИКОВ
Для оценки шумовых и переходных характеристик электрических схем необходимо учитывать реальные параметры проводников.
Одной из наиболее важных параметров проводника является индуктивность. Даже на низкой частоте проводник может иметь индуктивное сопротивление превышающее активное. Значение индуктивности проводника при приближении его к заземляющей поверхности – уменьшается, и наоборот, с удалением проводника от заземляющей поверхности его индуктивность увеличивается.
Вторая важная характеристика – сопротивление. Выбор диаметра проводника определяется в основном максимально-допустимым падением напряжения на нём. На высоких частотах, следует иметь ввиду что, вследствие скин-эффекта сопротивление проводника увеличивается. Скин-эффект обуславливает состояние проводника, при котором ток концентрируется вблизи поверхности проводника, что вызывается наличием магнитных полей, создаваемых протекающим в проводнике током. По мере увеличения частоты, ток концентрируется всё ближе к поверхности. Это уменьшает эффективное поперечное сечение, по которому течёт ток и тем самым увеличивает действующее значение сопротивления.
Сопротивление проводника переменному току можно уменьшить, изменив форму поперечного сечения проводника. Проводник с прямоугольным сечением оказывает переменному току меньшее сопротивление, чем с круглым, так как его поверхность на единицу площади поперечного сечения больше.
Так же можно отметить температурный коэффициент электрического сопротивления, который характеризует зависимость электрического сопротивления от температуры проводника. Для большинства металлов температурный коэффициент сопротивления положителен: их сопротивление растёт с ростом температуры. А для полупроводников без примесей он отрицателен.