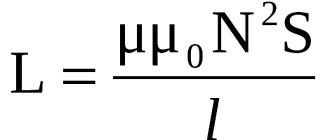Неразветвленная электрическая цепь
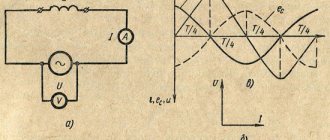
Неразветвленную электрическую цепь можно представить эквивалентной RLС-
цепью (рис. 3.20).
При синусоидальном напряжении
и напряжения на элементах
также синусоидальны, причем uL
и
uC
всегда находятся в противофазе.
Для мгновенных значений напряжений выполняется второй закон Кирхгофа:
который можно представить в комплексной форме
Характер комплексного сопротивленияцепи
меняется в зависимости от соотношения реактивных xL
и
xC
составляющих.
При ( ) сопротивление цепи имеет индуктивный характер. Его аргумент, равный углу сдвига фаз j
между током и приложенным напряжением , положителен (рис. 3.21).
При ( ) комплексное сопротивление цепи Z
имеет
емкостный характер, а его аргумент, равный углу сдвига фаз, отрицателен: (рис. 3.22).
При ( ) сопротивление цепи Z
имеет
активный характер, а .
Для неразветвленной цепи справедлив закон Ома:
Фазовые сдвиги между током и напряжениями на разных участках цепи различны, их соотношения поясняют векторные диаграммы для активно-индуктивной нагрузки (рис. 3.23), для активно-емкостной нагрузки (рис. 3.24, а
) и для активной нагрузки (рис. 3.24,
б
).
При построении диаграмм начальная фаза тока принята равной нулю, а угол сдвига фаз отложен от вектора тока против движения часовой стрелки.
Из диаграмм следует, что входное напряжение имеет активную и реактивную составляющие. Вектор активной составляющей является проекцией вектора на вектор тока и совпадает с ним по фазе. Вектор реактивной составляющей является проекцией вектора входного напряжения на направление, ортогональное вектору тока , и образует с ним фазовый сдвиг π/2
. При индуктивной нагрузке реактивное напряжение опережает на
π/2
, при емкостном характере отстает на
π/2
.
При равенстве емкостного и индуктивного сопротивлений реактивная составляющая сопротивления цепи , характер нагрузки – активный, а полное напряжение и ток совпадают по фазе.
Цепь при последовательном соединении элементов R
,
L
,
C
можно представить одной из трех эквивалентных схем замещения:
· последовательным соединением активного R
и индуктив- ного
L
элементов ( ) (см. рис. 3.23);
· последовательным соединением активного R
и емкостного
C
элементов ( ) (см. рис. 3.24,
а
);
· активным элементом R
( ) (см. рис. 3.24,
б
).
Угол сдвига фаз j
= arctg
(x/R)
между напряжением , приложенным к цепи, и током определяется отношением реактивной
x
иактивной
R
составляющих сопротивления цепи, а не свойствами источника питания.
Источник
Неразветвленные и разветвленные электрические цепи. Рисунок 2 — Разветвленная цепь
Рисунок 2 — Разветвленная цепь
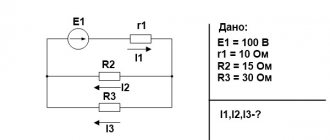
Электрические цепи подразделяют на неразветвленные и разветвленные. На рисунке 1 представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 2. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 2), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом
[править]Линейные и нелинейные электрические цепи
Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.
Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту от напряжения на этом компоненте называют вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.
В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.
Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие только резисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.
Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть прменён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные относятся практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).
5.Резистивный элемент, индуктивность, емкость. Определение и обозначение на электрических схемах. Какая энергия образуется и как она находится.
Резистивным называют идеализированный двухполюсный элемент, для которого связь между напряжением и током можно представить в виде графика, называемого вольт-амперной характеристикой (ВАХ)- Математическая модель резистивного элементаR определяется законом Ома, который устанавливает зависимость напряжения u от тока i, протекающего через сопротивление R.
, или .
Резистивный элемент моделирует процесс необратимого преобразования электромагнитной энергии в тепло и другие виды энергии, при этом запасание энергии в электромагнитном поле отсутствует.
Мощность, поглощаемая резистором
Условные обозначения резистивного (а), емкостного (б) и индуктивного (в) элементов.
Индуктивным элементом называется такой элемент электрической цепи, который обладает только свойством накопления энергии магнитного поля. Математической моделью индуктивного элемента L является вебер-амперная характеристика, которая устанавливает зависимость суммарного магнитного потока, образованного в витках катушки, (потокосцепления ψ) от величины протекающего через катушку тока i. Уравнение, описывающее свойства индуктивного элемента имеет вид:
, , где w – число витков катушки; n – номер витка, с которым сцеплен поток Фn, L – индуктивность катушки. Мощность электрических колебаний в индуктивном элементе под действием запасенной энергии согласно равна: , откуда .
Емкостным элементом называют элемент электрической цепи, обладающий только свойством накапливать энергию электрического поля. Математической моделью емкостного элемента С является вольт-кулоновая характеристика, которая устанавливает зависимость напряжения u от сообщенного емкости C электрического заряда q и определяется выражением:
, или .
Мощность электрических колебаний в емкостном элементе под действием запасенной в ней энергии к любому моменту времени t определяется выражением:
, откуда .
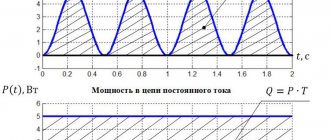
6.Работа резистивного элемента в цепи постоянного тока. Привести схему и временные диаграммы.
7.Работа емкости в цепи постоянного тока. Привести схему и временные диаграммы.
8.Работа индуктивности в цепи постоянного тока. Привести схему и временные диаграммы.
9.Работа резистивного элемента в электрических цепях переменного тока. Какая мощность определяется и чему она равна за период. Привести схему и временные диаграммы.
10.Работа емкости в электрических цепях переменного тока. Какая мощность определяется и чему она равна за период. Привести схему и временные диаграммы.
11.Работа индуктивности в электрических цепях переменного тока. Какая мощность определяется и чему она равна за период. Привести схему и временные диаграммы.
12.Электрическая цепь переменного тока с последовательным соединением элементов R, L, C. Привести схему цепи и вывод закона Ома для нее.
Векторная диаграмма
Определение 1
Неразветвленная электрическая цепь – это электрическая цепь, характеризующаяся тем, что на всех ее участках протекает один и тот же ток.
Пример простейшей неразветвленной электрической цепи изображен на рисунке ниже.
Рисунок 1. Неразветвленная электрическая цепь. Автор24 — интернет-биржа студенческих работ
Рассмотрим схему неразветвленной электрической цепи переменного тока, которая представлена на рисунке ниже.
Готовые работы на аналогичную тему
- Курсовая работа Расчет неразветвленной цепи переменного тока 430 руб.
- Реферат Расчет неразветвленной цепи переменного тока 230 руб.
- Контрольная работа Расчет неразветвленной цепи переменного тока 230 руб.
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Рисунок 2. Схема неразветвленной электрической цепи переменного тока. Автор24 — интернет-биржа студенческих работ
Вышепредставленная электрическая сеть состоит из следующих участков:
- Конденсатор (R1 X1).
- Катушки (R2 X2).
- Резистора (К3).
- Двух идеальных конденсаторов (Х4 и Х5).
Замечание 1
В данной электрической цепи конденсатор и катушка представлены активными и реактивными сопротивлениями.
Допустим, что нам, кроме сопротивлений, известен ток в цепи:
$i = Imsinwt$
Произвольно выбираем условно-положительное направление тока, по часовой стрелке. Для мгновенных величин, согласно второму закону Кирхгофа, уравнение напряжений, в векторном виде, будет выглядеть следующим образом:
Требуется консультация по учебной работе? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос
$U = U1a+U1p+U2a+U2p+U3a+U4p+U5p$
Численно, векторы напряжений определяются, как произведение сопротивления соответствующего участка цепи и тока. На рисунке ниже изображена векторная диаграмма, которая соответствует данному уравнению.
Рисунок 3. Векторная диаграмма. Автор24 — интернет-биржа студенческих работ
За исходный принимается вектор тока, а потом проводятся векторы падения напряжений для каждого участка цепи, направления векторов которых выбираются в соответствии с характером сопротивления. При построении векторной диаграммы напряжений выбирается точка б, которая совпадает с началом вектора тока. Затем из этой точки проводится вектор U5.2, представляющий собой вектор реактивного напряжения индуктивности и опережающий по фазе вектор тока на 90 градусов, между точками 5 и 6 на схеме. Из его конца проводится вектор реактивного напряжения емкости (U4p), который отстает от тока на 90 градусов, между точками 4 и 5 на схеме. После этого откладывается вектор активного напряжения на резисторе, совпадающий с вектором тока (U3a), между точками 3 и 4 на схеме и т.д., если следовать по цепи противоположно направлению тока. Те точки, в которых сходятся начало следующего и конец предыдущего векторов, обозначаются такими же номерами, каким обозначены на схеме.
При данном построении векторной диаграммы, напряжение между двумя любыми точками рассматриваемой цепи возможно определить по фазе и величине, посредством проведения вектора на диаграмме между точками с такими же номерами. Например, напряжение между точками 5 и 2 можно выразить вектором, который проводится из точки 2 в точку 5 и т.д.
Определение 2
Топографическая векторная диаграмма – это векторная диаграмма, которая была построена в соответствии с чередованием составляющих электрической цепи.