Сдвиг фаз переменного тока и напряжения
Мощность постоянного тока, как мы уже знаем, равна произведению напряжения на силу тока. Но при постоянном токе направления тока и напряжения всегда совпадают. При переменном же токе совпадение направлений тока и напряжения имеет место только в случае отсутствия в цепи тока конденсаторов и катушек индуктивности.
Для этого случая формула мощности
На рисунке 1 представлена кривая изменения мгновенных значений мощности для этого случая (направление тока и напряжения совпадают). Обратим внимание на то обстоятельство, что направления векторов напряжения и тока в этом случае совпадают, то есть фазы тока и напряжения всегда одинаковы.
Рисунок 1. Сдвиг фаз тока и напряжения. Сдвига фаз нет, мощность все время положительная.
При наличии в цепи переменного тока конденсатора или катушки индуктивности, фазы тока и напряжения совпадать не будут.
О причинах этого несовпадения читайте в моем учебники для емкостной цепи и для индуктивной цепи, а сейчас установим, как будет оно влиять на величину мощности переменного тока.
Представим себе, что при начале вращения радиусы-векторы тока и напряжения имеют различные направления. Так как оба вектора вращаются с одинаковой скоростью, то угол между ними будет оставаться неизменным во все время их вращения. На рисунке 2 изображен случай отставания вектора тока Im от вектора напряжения Um на угол в 45°.
Рисунок 2. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 45, мощность в некоторые периоды времени становиться отрицательной.
Рассмотрим, как будут изменяйся при этом ток и напряжение. Из построенных синусоид тока и напряжения видно, что когда напряжение проходит через ноль, ток имеет отрицательное значение.
Затем напряжение достигает своей наибольшей величины и начинает уже убывать, а ток хотя и становится положительным, но еще не достигает наибольшей величины и продолжает возрастать. Напряжение изменило свое направление, а ток все еще течет в прежнем направлении и т. д. Фаза тока все время запаздывает по сравнению с фазой напряжения. Между фазами напряжения и тока существует постоянный сдвиг, называемый сдвигом фаз.
Действительно, если мы посмотрим на рисунок 2, то заметим, что синусоида тока сдвинута вправо относительно синусоиды напряжения. Так как по горизонтальной оси мы откладываем градусы поворота, то и сдвиг фаз можно измерять в градусах. Нетрудно заметить, что сдвиг фаз в точности равен углу между радиусами-векторами тока и напряжения.
Вследствие отставания фазы тока от фазы напряжения его направление в некоторые моменты не будет совпадать с направлением напряжения. В эти моменты мощность тока будет отрицательной, так как произведение положительной величины на отрицательную величину всегда будет отрицательным. Эта значит, что внешняя электрическая цепь в эти моменты становится не потребителем электрической энергии, а источником ее. Некоторое количество энергии, поступившей в цепь во время части периода, когда мощность была положительной, возвращается источнику энергии в ту часть периода, когда мощность отрицательна.
Чем больше сдвиг фаз, тем продолжительнее становятся части периода, в течение которых мощность делается отрицательной, тем, следовательно, меньше будет средняя мощность тока.
При сдвиге фаз в 90° мощность в течение одной четверти периода будет положительной, а в течение другой четверти периода — отрицательной. Следовательно, средняя мощность тока будет равна нулю, и ток не будет производить никакой работы (рисунок 3).
Рисунок 3. Сдвиг фаз тока и напряжения. Фазы тока и напряжения сдвинуты на 90, мощность в течении одной четвери периода положительна, а в течении другой отрицательна. В среднем мощьноть равна нулю.
Теперь ясно, что мощность переменного тока при наличии сдвига фаз будет меньше произведения эффективных значений тока и напряжения, т. е. формулы
в этом случае будут неверны
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник
Сдвиг фаз между током и напряжением. Понятие двухполюсника
к оглавлению
Рассмотрим электрическую цепь состоящую из последовательно включенных сопротивления r
, индуктивности
L
и емкости
C
(рис. 1 а)).
Протекающий ток i
создает на всех элементах цепи падения напряжения, сумма которых равна напряжению на входе
u
. Для синусоидальных функций времени это можно записать в виде выражения
| . | (1) |
Пусть ток в цепи равен i
=
Im
sin(w
t
+y
i
). Подставим это выражение в (1) и получим:
| . | (2) |
Очевидно, что определить из выражения (2) амплитуду и начальную фазу напряжения u
сложно. Поэтому перейдем в выражении (1) от оригиналов величин к их символическим изображениям комплексными числами или векторами.
| . | (3) |
Формально выражение (3) совпадает с записью закона Ома для цепи постоянного тока. Отличие заключается в том, что все величины входящие в него являются комплексными числами изображающими реальные функции времени. Поэтому его можно назвать законом Ома в области изображений
.
Графически выражение (3) можно представить векторной диаграммой рис. 1 б). Здесь вектор входного напряжения U
складывается из трех составляющих. Вектор падения напряжения на резистивном сопротивлении
rI
совпадает по направлению с током
I
, т.к. отличается от него только вещественным коэффициентом
r
. Вторая составляющая
jxLI
перпендикулярна вектору тока
I
и опережает его по фазе на 90°. Это связано с умножением на оператор поворота
j
вектора
xLI
, совпадающего по направлению с током. Третий вектор —
jxСI
отстает по фазе от тока на 90° , т.к. образуется из него умножением на оператор поворота —
j
.
Величина Z
=
r
+
j
(
xL
—
xC
) =
r
+
jx
=
Ze jj
в выражении (3), имеющая размерность сопротивления, называется
комплексным сопротивлением
. Его вещественная часть
r
называется
резистивным сопротивлением
, а мнимая
x
=
xL
—
xC
—
реактивным сопротивлением
. Из выражения (3) следует, что комплексное сопротивление является отношением комплексного падения напряжения к комплексному току
| , | (4) |
поэтому его модуль Z
можно определить через отношение модулей напряжения и тока
Z
=
U
/
I
или через резистивную и реактивную составляющую .
Модуль комплексного сопротивления называется полным сопротивлением
.
Аргумент комплексного сопротивления φ есть разность начальных фаз напряжения и тока, но его можно также определить по вещественной и мнимой составляющим комплексного сопротивления как φ = arctg(X
/
R
). Следовательно,
сдвиг фаз между напряжением и током определяется только параметрами нагрузки и не зависит от параметров тока и напряжения в цепи
. Из выражения (4) необходимо следует, что положительные значения φ соответствуют отставанию тока по фазе, а отрицательные — опережению.
Таким образом, изображение напряжения на входе цепи можно представить через комплексное сопротивление в виде
| . | (5) |
Теперь можно вернуться к определению оригинала напряжения u
на входе цепи рис. 1 а) преобразованием изображения (5) —
| . | (6) |
Из выражения (3) можно представить комплексное сопротивление суммой трех величин в виде
| Z = | (7) |
и изобразить эти соотношения на векторной диаграмме (рис. 1 в)). Векторная диаграмма сопротивлений подобна векторной диаграмме напряжений, т.к. комплексное сопротивление Z
аналитически можно получить делением комплексного напряжения
U
на комплексный ток
I
. Графически это соответствует повороту векторной диаграммы напряжений на угол -y
i
и изменению ее масштаба на 1/
I
.
Соотношение между напряжением и током в электрической цепи можно выразить также величиной обратной сопротивлению
| . | (8) |
Величина Y
называется
комплексной проводимостью
. Ее модуль является величиной обратной модулю комплексного сопротивления, а
аргумент всегда
равен его аргументу, но
имеет противоположный знак
.
Вещественная составляющая комплексной проводимости называется резистивной проводимостью
, а мнимая —
реактивной проводимостью
.
Между резистивными (R
и
G
) и реактивными (
X
и
B
)составляющими комплексной проводимости и сопротивления существует очевидное соответствие, вытекающее из понятия комплексного числа.
| . | (9) |
Отсюда следует:
- резистивные и реактивные составляющие комплексного сопротивления и проводимости в общем случаене являются взаимно обратными величинами
; - резистивные и реактивные составляющие комплексного сопротивления и проводимости являются взаимно обратными величинами только в случае отсутствия второй составляющей
; - реактивные составляющие комплексного сопротивления и проводимости всегда противоположного знака
.
ЗАДАЧА 1
Угол сдвига фаз между напряжением и током в электрической цепи определяется аргументом ее комплексного сопротивления φ . Поэтому при анализе цепи часто бывает достаточно определить характер изменения этого угла при вариации некоторого параметра.
Комплексное сопротивление любого участка электрической цепи в общем случае имеет вещественную и мнимую составляющие Z
=
R
+
jX
. Построим вектор
Z
на комплексной плоскости и проанализируем его поведение при вариации составляющих
R
и
X
.
Пусть R=
const, а
X
=var. Тогда конец вектора
Z
будет скользить по прямой
R=
const (рис. 2). При
X
= 0 сопротивление
Z
вещественное, т.е. чисто резистивное и сдвиг фаз между током и напряжением φ равен нулю.
Если X(r) µ , то вектор Z
поворачивается в положительном направлении и его аргумент в пределе стремится к p /2. Это означает, что пределом
Z
является комплексное индуктивное сопротивление.
При X(r) — µ , пределом вектора Z
является бесконечно большое комплексное емкостное сопротивление.
Таким образом, изменение реактивного сопротивления в пределах — µ < X
< + µ приводит к изменению угол сдвига фаз между током и напряжением в пределах — p /2 < φ < + p /2.
Рассматривая аналогичным образом вариации резистивного сопротивления R
=var при постоянном положительном (рис. 3 а)) и отрицательном (рис. 3 б)) реактивном сопротивлении
X
, можно прийти к выводу, что в этом случае угол сдвига фаз между током и напряжением будет меняться соответственно в пределах +p /2 < φ <0 и — p /2 < φ < 0.
ЗАДАЧА 2
Любой участок электрической цепи, имеющий только две точки подключения, называется двухполюсником
. Через эти две точки в общем случае протекает электрический ток и существует некоторое падение напряжения. Если рассматриваемый участок электрической
цепи не содержит источников электрической энергии
, то такой двухполюсник называется
пассивным
.
Приналичии
одного или более
источников энергии
в двухполюснике он называется
активным
.
Если представить ток и напряжение на пассивном двухполюснике изображающими комплексными числами U
и
I
(рис. 4), то их отношение будет комплексным сопротивлением
Z
или комплексной проводимостью
Y
и все рассмотренные выше соотношения будут справедливы по отношению к ним. Это означает, что в зависимости от параметров элементов образующих двухполюсник, их числа и схемы соединения,
аргумент Z может находиться в пределах —
p /2 < φ < + p /2
.
Предельными значениями для него будут углы φ = — p /2, φ = + p /2 и φ = 0. Первые два значения соответствуют комплексным емкостному и индуктивному сопротивлениям. Фазовый сдвиг в 90° возможен только при условии, что внутри двухполюсника отсутствуют резистивные сопротивления. В дальнейшем будет показано, что в любой электрической цепи резистивная составляющая комплексного сопротивления связана с тепловыми потерями. Поэтому ее отсутствие означает отсутствие потерь энергии, что в нормальных условиях протекания электромагнитных процессов невозможно. Следовательно, невозможен и фазовый сдвиг между током и напряжением в 90° . Однако в реальных устройствах, в особенности в конденсаторах, потери могут быть столь незначительными, что ими можно пренебречь и считать двухполюсник чисто реактивным.
Рассмотренные закономерности позволяют представить любой сколь угодно сложный пассивный двухполюсник эквивалентным набором не более, чем двух элементов, который обеспечивает такую же связь между током и напряжением на входе, как исходный двухполюсник. Для этого достаточно знать модули тока и напряжения на входе и сдвиг фаз между ними. Все возможные варианты замещения двухполюсника приведены в таблице 1.
Таблица 1.
| Фазовый сдвиг φ | Комплексное сопротивление двухполюсника Z | Область возможных значений Z | Схема замещения | Название двухполюсника |
| j =p /2 | Z=jw L = | Индуктивный | ||
| 0 < φ < p /2 | Z = R + | Резистивно-индуктивный | ||
| j =0 | Z = R | Резистивный | ||
| 0 >φ >-p /2 | Z = R- jXC | Резистивно-емкостной | ||
| j = — p /2 | Z = — j /(w | Емкостной |
Во многих случаях характер двухполюсника можно определить по составу элементов электрической схемы. Отсутствие реактивных элементов в схеме всегда позволяет представить двухполюсник эквивалентным резистивным сопротивлением. Наличие резисторов и реактивных элементов одного из типов (только индуктивностей или только емкостей), также позволяет однозначно представить двухполюсник в виде совокупности резистора и соответствующего реактивного элемента, тип которого всегда соответствует типу реактивных элементов исходной схемы. Наличие в схеме двухполюсника реактивностей противоположных типов не позволяет определить тип двухполюсника без расчета значения φ, однако после расчета он также может быть заменен схемой замещения, соответствующей типу его эквивалентной реактивности.
ЗАДАЧА 3
В таблице 1 резистивно-индуктивный и резистивно-емкостной двухполюсники представлены двумя схемами — последовательной и параллельной. Они содержат реактивный элемент и резистор. Такому представлению соответствует учет потерь энергии в электромагнитных процессах
, изображаемых на электрических схемах индуктивностью или емкостью.
Дело в том, что при любых электромагнитных процессах происходят необратимые потери энергии, связанные с преобразованием в тепло. Мощность этих потерь, в соответствии с законом Джоуля-Ленца, равна I
2
R
или
U
2/
R
, где
I
и
U
— действующие значения тока и напряжения на участке электрической цепи, а
R
— его резистивное сопротивление. Однако резистивное сопротивление не обязательно должно быть сопротивлением проводника или проводящей среды. Сопротивлением можно представить даже процесс преобразования в тепло, не связанный в явном виде с протеканием электрического тока. Резистором можно также учесть механическую работу, совершаемую электромагнитными силами. При таких представлениях достаточно, чтобы соблюдалось равенство мощности выделяющейся в резисторе и в реальном процессе.
По соображениям удобства решения конкретной задачи, резистор можно подключить последовательно или параллельно реактивному элементу (L
или
C
).
Тогда из выражений (9) соотношения между параметрами последовательной и параллельной схем замещения для рис. 5 а) будут
| (10) |
а для рис. 5 б) —
| (11) |
Из выражений (10) и (11) следует, что параметры элементов эквивалентных схем
при взаимных преобразованиях
зависят
не только от параметров элементов исходной схемы, но и
всегда от частоты
.
к оглавлению
Ток опережает напряжение формула
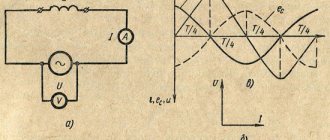
Проделаем следующий опыт. Возьмем описанный в § 153 осциллограф с двумя петлями и включим его в цепь так (рис. 305,а), чтобы петля 1 была включена в цепь последовательно с конденсатором, а петля 2 параллельно этому конденсатору. Очевидно, что кривая, получаемая от петли 1, изображает форму тока, проходящего через конденсатор, а от петли 2 дает форму напряжения между обкладками конденсатора (точками и ), потому что в этой петле осциллографа ток в каждый момент времени пропорционален напряжению. Опыт показывает, что в этом случае кривые тока и напряжения смещены по фазе, причем ток опережает по фазе напряжение на четверть периода (на ). Если бы мы заменили конденсатор катушкой с большой индуктивностью (рис. 305,б), то оказалось бы, что ток отстает по фазе от напряжения на четверть периода (на ). Наконец, таким же образом можно было бы показать, что в случае активного сопротивления напряжение и ток совпадают по фазе (рис. 305,в).
Рис. 305. Опыт по обнаружению сдвига фаз между током и напряжением: слева – схема опыта, справа – результаты
В общем случае, когда участок цепи содержит не только активное, но и реактивное (емкостное, индуктивное или и то и другое) сопротивление, напряжение между концами этого участка сдвинуто по фазе относительно тока, причем сдвиг фаз лежит в пределах от до и определяется соотношением между активным и реактивным сопротивлениями данного участка цепи.
В чем заключается физическая причина наблюдаемого сдвига фаз между током и напряжением?
Если в цепь не входят конденсаторы и катушки, т. е. емкостным и индуктивным сопротивлениями цепи можно пренебречь по сравнению с активным, то ток следует за напряжением, проходя одновременно с ним через максимумы и нулевые значения, как это показано на рис. 305,в.
Если цепь имеет заметную индуктивность , то при прохождении по ней переменного тока в цепи возникает э. д. с. самоиндукции. Эта э. д. с. по правилу Ленца направлена так, что она стремится препятствовать тем изменениям магнитного поля (а следовательно, и изменениям тока, создающего это поле), которые вызывают э. д. с. индукции. При нарастании тока э. д. с. самоиндукции препятствует этому нарастанию, и потому ток позже достигает максимума, чем в отсутствие самоиндукции. При убывании тока э. д. с. самоиндукции стремится поддерживать ток и нулевые значения тока будут достигнуты в более поздний момент, чем в отсутствие самоиндукции. Таким образом, при наличии индуктивности ток отстает по фазе от тока в отсутствие индуктивности, а следовательно, отстает по фазе от своего напряжения.
Если активным сопротивлением цепи можно пренебречь по сравнению с ее индуктивным сопротивлением , то отставание тока от напряжения по времени равно (сдвиг фаз равен ), т. е. максимум совпадает с , как это показано на рис. 305,б. Действительно, в этом случае напряжение на активном сопротивлении , ибо , и, следовательно, все внешнее напряжение уравновешивается э. д. с. индукции, которая противоположна ему по направлению: . Таким образом, максимум совпадает с максимумом , т. е. наступает в тот момент, когда изменяется быстрее всего, а это бывает, когда . Наоборот, в момент, когда проходит через максимальное значение, изменение тока наименьшее , т. е. в этот момент .
Если активное сопротивление цепи не настолько мало, чтобы им можно было пренебречь, то часть внешнего напряжения падает на сопротивлении , а остальная часть уравновешивается э. д. с. самоиндукции: . В этом случае максимум отстоит от максимума по времени меньше, чем на (сдвиг фаз меньше ), как это изображено на рис. 306. Расчет показывает, что в этом случае отставание по фазе может быть вычислено по формуле
При имеем и , как это объяснено выше.
Рис. 306. Сдвиг фаз между током и напряжением в цепи, содержащей активное и индуктивное сопротивления
Если цепь состоит из конденсатора емкости , а активным сопротивлением можно пренебречь, то обкладки конденсатора, присоединенные к источнику тока с напряжением , заряжаются и между ними возникает напряжение . Напряжение на конденсаторе следует за напряжением источника тока практически мгновенно, т. е. достигает максимума одновременно с и обращается в нуль, когда .
Зависимость между током и напряжением в этом случае показана на рис. 307,а. На рис. 307,б условно изображен процесс перезарядки конденсатора, связанный с появлением переменного тока в цепи.
Рис. 307. а) Сдвиг фаз между напряжением и током в цепи с емкостным сопротивлением в отсутствие активного сопротивления. б) Процесс перезарядки конденсатора в цепи переменного тока
От чего зависит угол сдвига фаз напряжения и тока в цепи
От величины активного, индуктивного и ёмкостного сопротивления. tg w = (X-C)/R. Где w — угол сдвига фаз, X — индуктивное сопротивление, C- ёмкостное сопротивление, R- активное сопротивление.
Угол сдвига фаз между напряжением и током в электрической цепи определяется аргументом ее комплексного сопротивления . Поэтому при анализе цепи часто бывает достаточно определить характер изменения этого угла при вариации некоторого параметра.
Пусть R=
const, а
X
=var. Тогда конец вектора
Z
будет скользить по прямой
R=
const (рис. 2). При
X
= 0 сопротивление
Z
вещественное, т.е. чисто резистивное и сдвиг фаз между током и напряжением равен нулю.
Аналитический расчет токи в цепи по методу узловых напряжений
Метод узловы́х потенциалов — метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.
Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно
Перед началом расчёта выбирается один из узлов (базовый узел), потенциал которого считается равным 0. Затем узлы нумеруются, после чего составляется система уравнений.
Уравнения составляются для каждого узла, кроме базового. Слева от знака равенства записывается:
потенциал рассматриваемого узла, умноженный на сумму проводимостей ветвей, примыкающих к нему;
минус потенциалы узлов, примыкающих к данному, умноженные на проводимости ветвей, соединяющих их с данным узлом.
Справа от знака равенства записывается:
сумма всех источников токов, примыкающих к данному узлу;
сумма произведений всех ЭДС, примыкающих к данному узлу, на проводимость соответствующего звена.
Если источник направлен в сторону рассматриваемого узла, то он записывается со знаком «+», в противном случае — со знаком «−».
Проверка баланса мощностей
Баланс мощностей является следствием закона сохранения энергии — суммарная мощность вырабатываемая (генерируемая) источниками электрической энергии равна сумме мощностей потребляемой в цепи.
Баланс мощностей используют для проверки правильности расчета электрических цепей.
Здесь мы рассмотрим баланс для цепей постоянного тока.
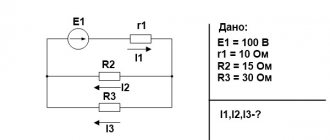
Например. У нас есть электрическая цепь.
Для проверки правильности решения составляем баланс мощностей.
Источники E1 и E2 вырабатывают электрическую энергию, т.к. направление ЭДС и тока в ветвях с источниками совпадают (если ЭДС и ток в ветвях направлены в противоположную сторону, то источник ЭДС потребляет энергию и его записывают со знаком минус). Баланс мощностей для заданной цепи запишется так:
Что такое реактивная мощность и как её рассчитать?
Многие потребители электроэнергии не подозревают того, что часть учтённого электричества расходуется бесполезно. В зависимости от вида нагрузки уровень потерь электроэнергии может достигать от 12 до 50%. При этом счетчики электроэнергии засчитывают эти потери, относя их к полезной работе, за что приходится платить. Виной завышения оплаты за потребление электроэнергии, не выполняющей полезной работы, является реактивная мощность, присутствующая в сетях переменных токов.
Чтобы понять, за что мы переплачиваем и как компенсировать влияние реактивных мощностей на работу электрических установок, рассмотрим причину появления реактивной составляющей при передаче электроэнергии. Для этого придётся разобраться в физике процесса, связанного с переменным напряжением.
Угол сдвига фаз между током и напряжением
Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Что такое реактивная мощность?
Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.
При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.
На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.
К устройствам с индуктивными нагрузками относятся:
- электромоторы;
- дроссели;
- трансформаторы;
- электромагнитные реле и другие устройства, содержащие обмотки.
Ёмкостными сопротивлениями обладают конденсаторы.
Физика процесса
Когда мы имеем дело с цепями постоянного тока, то говорить о реактивной мощности не приходится. В таких цепях значения мгновенной и полной мощности совпадают. Исключением являются моменты включения и отключения ёмкостных и индуктивных нагрузок.
Похожая ситуация происходит при наличии чисто активных сопротивлений в синусоидальных цепях. Однако если в такую электрическую цепь включены устройства с индуктивными или ёмкостными сопротивлениями, происходит сдвиг фаз по току и напряжению (см. рис.1).
При этом на индуктивностях наблюдается отставание тока по фазе, а на ёмкостных элементах фаза тока сдвигается так, что ток опережает напряжение. В связи с нарушением гармоники тока, полная мощность разлагается на две составляющие. Ёмкостные и индуктивные составляющие называют реактивными, бесполезными. Вторая составляющая состоит из активных мощностей.
Рис. 1. Сдвиг фаз индуктивной нагрузкой
Угол сдвига фаз используется при вычислениях значений активных и реактивных ёмкостных либо индуктивных мощностей. Если угол φ = 0, что имеет место при резистивных нагрузках, то реактивная составляющая отсутствует.
Важно запомнить:
- резистор потребляет исключительно активную мощность, которая выделяется в виде тепла и света;
- катушки индуктивности провоцируют образование реактивной составляющей и возвращают её в виде магнитных полей;
- Ёмкостные элементы (конденсаторы) являются причиной появления реактивных сопротивлений.
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.
Рис. 2. коэффициент мощности
Применяя теорему Пифагора, вычислим модуль вектора S:
Отсюда можно найти реактивную составляющую:
Реактивная составляющая
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Способы компенсации
Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.
Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.
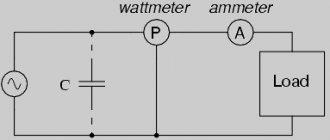
На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.
Рис. 3. Устройство компенсации
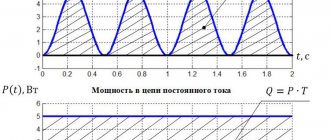
Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).
Рис. 4. Компенсация реактивной мощности с помощью конденсаторов
Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.
Методы измерения угла сдвига фаз
Существует несколько способов измерения угла сдвига фаз, это:
- Использование двухлучевого или двухканального осциллографа.
- Компенсационный метод основан на сравнении измеряемого фазового сдвига, с фазовым сдвигом, который предоставляется образцовым фазовращателем.
- Суммарно-разностный метод, он заключается в использовании гармонических или сформированных прямоугольных сигналов.
- Преобразование сдвига фаз во временном интервале.
Нужны ли устройства компенсации в быту?
На первый взгляд в домашней сети не должно быть больших реактивных токов. В стандартном наборе бытовых потребителей преобладают электрическая техника с резистивными нагрузками:
- электрочайник (Pf = 1);
- лампы накаливания (Pf = 1);
- электроплита (Pf = 1) и другие нагревательные приборы;
Коэффициенты мощности современной бытовой техники, такой как телевизор, компьютер и т.п. близки к 1. Ими можно пренебречь.
Но если речь идёт о холодильнике (Pf = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.