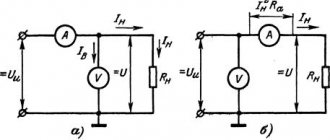
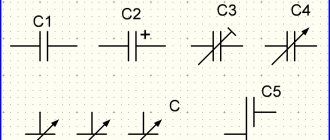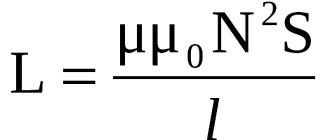При определенном сочетании частоты сигнала и реактивного сопротивления образуется резонанс в электрической цепи. Радиолюбители применяют его для настройки на определенную передающую станцию. Конструкторы линий электропередач делают специальные расчеты, чтобы предотвратить броски напряжения и аварийные ситуации. Представленные ниже сведения помогут успешно решать практические задачи на основе особенностей этого явления.
При резонансе в цепи переменного тока резко увеличивается амплитуда сигнала
Причины резонанса
Классический пример с приказом командира идти марширующим солдатам «не в ногу» перед мостом наглядно демонстрирует суть этого явления. Если не использовать такую предосторожность, колебания могут увеличиться до критичного значения, вплоть до разрушения конструкции. Для получения максимальной амплитуды раскачивают в определенном ритме качели. Приведенные примеры демонстрируют существенное увеличение результата при совпадении частот внешнего воздействия и непосредственно самой системы.
Электрический резонанс по своим принципам не отличается от механических аналогов. Он образуется при совпадении частот внешнего сигнала и контура. Функции накопителей энергии выполняют реактивные индукционные и емкостные элементы. Потери (постепенное уменьшение амплитуды) обеспечивает электрическое сопротивление цепи, что аналогично коэффициенту трения.
Принцип резонанса токов
Резонанс — что это такое
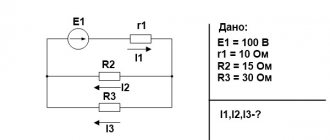
Для создания необходимых условий электро резонанса необходимо создать параллельный контур с тремя типовыми компонентами:
- сопротивлением (R);
- емкостью (C);
- индуктивностью (L).
Схему подключают к источнику питания с напряжением (U)
На определенной частоте суммарные стоки через реактивные элементы (IL, Ic) становятся значительно больше, чем ток источника (I). Это явление называют резонансом тока.
Характеристики резонанса
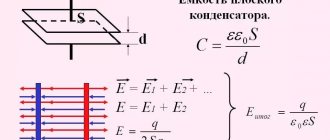
Конденсатор в цепи переменного тока
Это явление образуется при одинаковых реактивных составляющих цепи. Такое распределение позволяет обеспечить равномерную циркуляцию магнитной и электрической составляющих энергии (через индуктивность и конденсатор, соответственно). Такой контур называют «колебательным» по аналогии с механическим маятником.
При достижении определенной резонансной частоты (w) в параллельном (последовательном) контуре импеданс максимален (минимален). Соответствующим образом при изменении электрического сопротивления уменьшается (увеличивается) ток.
Резонанс токов и напряжений
Механический резонанс
Параллельный контур используют, чтобы создать резонанс тока. Для выполнения отмеченных выше условий выбирают равные значения реактивных проводимостей (BL и Bc). По мере увеличения частоты общее сопротивление контура возрастает, что сопровождается уменьшением силы тока.
График изменения тока и проводимости, формулы для расчетов
В последовательном резонансном контуре устанавливают аналогичные функциональные компоненты. Эта схема при достижении резонансной частоты уменьшает сопротивление, что сопровождается существенным увеличением напряжения на реактивных составляющих, по сравнению с электродвижущей силой источника питания.
Резонанс напряжений в цепи переменного тока: график, электрическая схема и формула расчета
Занятие 44 Резонанс напряжений
2015-04-01 3201
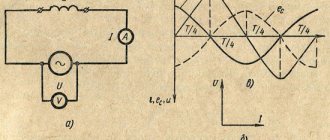
Схема последовательного соединения активного сопротивления, катушки индуктивности и конденсатора приведена на рис.44.1.
Рис. 44.1. Схема последовательного соединения активного сопротивления, катушки индуктивности и конденсатора
При последовательном соединении трех элементов R, L, C векторная диаграмма выглядит следующим образом: вектор тока в цепи I отложен горизонтально, с ним совпадает вектор напряжения на активном сопротивлении UR, вектор напряжения на индуктивности U L направлен вверх, а вектор напряжения на емкости UC направлен вниз.
Рис.44.2. Векторная диаграмма напряжений при последовательном соединении активного сопротивления, катушки индуктивности и конденсатора.
Если падение напряжения на индуктивном сопротивлении больше, чем на емкостном, то результирующий вектор будет опережать вектор тока на какой-то угол φ. В этом случае говорят, что цепь имеет индуктивный характер. (см.рис.44.3.)
Рис.44.3. Векторная диаграмма цепи с индуктивным характером.
Если падение напряжения на емкостном сопротивлении больше, чем на индуктивном, то вектор результирующего напряжения будет отставать от вектора тока на какой –то угол φ. В этом случае говорят, что цепь носит емкостный характер. (см. рис.44. 4.)
Рис.44.4. Векторная диаграмма цепи с емкостным характером.
В общем случае уравнение напряжений в цепи будет равно:
а уравнение сопротивлений :
Особенностью последовательного соединения активного сопротивления, емкости и индуктивности является возможность возникновения резонанса напряжений.
Представим, что в цепи с последовательно соединенными активным сопротивлением, емкостью и индуктивностью, частота тока увеличивается от частоты f1 до частоты f2. (см. рис. 44.5.)
Рис.44.5. Изменение реактивных сопротивлений при изменении частоты тока.
При увеличении частоты тока в цепи емкостное сопротивление уменьшается, а индуктивное увеличивается. При каком – то значении частоты тока емкостное сопротивление становится равным индуктивному сопротивлению. Эта частота называется резонансной. Явления, происходящие в цепи с последовательно соединенными R,L,C при резонансной частоте называются резонансом напряжения.
При резонансе напряжение на емкости UC равно напряжению на индуктивности U L . Но так как они находятся в противофазе друг другу сумма их равна нулю.
Условием резонанса является равенство реактивных сопротивлений XL = XC или
Отсюда значение резонансной частоты определиться
Когда цепь не настроена в резонанс , ее полное сопротивление определяется соотношением:
, при резонансе, когда XL = XC, полное сопротивление цепи будет равно :
Таким образом полное сопротивление цепи при резонансе оказывается равным активному сопротивлению.
Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает.
.На векторной диаграмме при резонансе (см.рис.44. 6) векторы напряжений на реактивных элементах равны друг другу и направлены в противоположные стороны. т. е. сдвинуты по фазе относительно друг друга на угол 180 градусов. Угол сдвига фаз между током и напряжением в сети равен нулю.
Рис.44.6. Векторная диаграмма при резонансе напряжений.
Рис.44.7. Изменение тока в цепи при резонансе.
Источник
RLC-цепь
Для уточнения процессов надо изучить особенности компонентов типовой RLC цепи. Если к источнику переменного тока подсоединить конденсатор, напряжение на его обмотках будет изменяться по аналогии с исходным сигналом. Для расчетов пользуются понятием емкостного сопротивления Xc, которое определяется формулой:
Xc = 1/2π * f * C,
где:
- f – частота;
- С – емкость.
По мере роста частоты увеличивается емкостное сопротивление, и уменьшается ток:
I = U/ Xc.
Этот элемент выполняет определенные ограничительные функции. Однако он не рассеивает энергию c преобразованием в тепло как обычное электрическое сопротивление R.
К сведению. Для упрощения здесь рассмотрена идеальная емкость. В действительности каждый электронный компонент создает активное сопротивление току, что в определенной ситуации сопровождается нагревом.
Для расчета влияния индуктивной составляющей применяют формулы:
- XL = 2π * f * L;
- I = U/XL;
- I = U/2π * f * L.
При подключении катушки к источнику питания образуется магнитное поле, которое препятствует прохождению тока. Формулы демонстрируют прямую зависимость сопротивления от частоты и значения индуктивности (L).
Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC..
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC..=Umaxcos.ωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcos.ωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsin.ωt=CUmaxcos.(ωt+π2..)
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2.. (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω..=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Определение
I=UXC..
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C..=LI2max2..
Отсюда:
LC=q2maxI2max..
√LC=qmaxImax..
T=2π√LC=2πqmaxImax..=2·3,1410−610−3..≈6,3·10−3 (с)
Электрический резонанс
Для полноценного изучения (применения) явления надо учитывать полное сопротивление цепи (Z). Вместе с потерями его можно выразить следующей формулой при последовательном подключении функциональных элементов:
Z = √ R2 + (2π * f * L — 1/2π * f * C)2.
По закону Ома:
I = U/Z = U/ √ R2 + (2π * f * L — 1/2π * f * C)2.
Если соблюдается равенство реактивных составляющих, сопротивление уменьшается с одновременным увеличением силы тока. При соблюдении такого условия несложно вычислить резонансную частоту (Fрез):
- 2π * f * L = 1/2π * f * C;
- Fрез = 1/2π * √ L*C.
Резонанс напряжений, достигающих максимальной амплитуды
Получить наибольшую амплитуду в последовательном контуре можно с помощью изменения следующих параметров:
- индуктивности;
- емкости;
- частоты.
Значения отдельных компонентов устанавливают с применением рассмотренных выше формул. Так, величину емкости можно вычислить следующим образом:
C = 1/ f2 * L.
Если реактивные компоненты значительно больше активного сопротивления, на клеммах конденсатора или катушки можно получить повышение напряжения, по сравнению с источником.
Резонанс токов через реактивные элементы
В параллельном контуре оперируют с понятиями реактивных проводимостей (BL и Bc). Как и в предыдущем примере, для создания резонансного режима необходимо обеспечить равенство этих параметров. Дополнительным условием является совпадение частот (источника и контура). Ток при резонансе будет проходить только через активное сопротивление R.
Параллельный резонанс при источнике ЭДС
Добротность для параллельной схемы вычисляют по формуле Q=R√C/L. При равенстве частот (источника и контура) сопротивление в отдельных ветвях не различается. Одинаковые значения токов создают компенсированные реактивные параметры конденсатора и катушки.
При отклонении частоты от резонансного значения в нижний (верхний) диапазон сопротивление приобретает емкостной (индуктивный) характер, соответственно. В обычном рабочем цикле происходит энергетический обмен между реактивными элементами цепи. Этот режим характеризуется увеличением в Q раз тока, проходящего по внутреннему контуру, по сравнению с поступающим от источника ЭДС. Идеальные условия, когда добротность стремится к бесконечной величине, невозможны. Прямые и паразитные потери в цепях ограничивают рост силы резонансного тока.
Применение резонансного явления
Резонанс в электрических цепях используют для фильтрации сигналов. Выбирают соответствующую схему обработки для ограничения необходимого диапазона либо расширения полосы пропускания.
С помощью последовательного контура можно повысить напряжение питания, если снабжающая организация не обеспечивает стабильность параметров сети. Такие неприятности встречаются при подключении потребителей на дачных участках и в коттеджных поселках, в сравнительно небольших населенных пунктах.
Недостаток ликвидируют конденсаторами, которые добавляют в электрическую цепь. Подобные решения помогают восстановить работоспособность дрели, станка, другого мощного оборудования. Обмотки соответствующего привода выполняют функции индуктивного компонента колебательного контура.
Параллельное подключение конденсаторов компенсирует потери, созданные реактивной мощностью. Этот вариант обеспечивает циркуляцию энергии между накопителем и подключенной обмоткой. Без такого дополнения часть энергии будет бесполезно потребляться сетью питания. Следует подчеркнуть, что счетчик в любом случае фиксирует потребление. Данная модернизация поможет сэкономить на оплате коммунальных услуг.
Резонансные явления способны чрезмерно увеличить силу тока или напряжение. Необходим точный расчет электрических цепей, чтобы предотвратить перегрев и повреждение проводов, короткие замыкания и другие аварийные ситуации.
Использование резонанса напряжений для передачи радиосигнала
Применение последовательного колебательного контура удобно изучать на конкретном примере. При конструировании передающих устройств, например, уменьшение импеданса на определенной частоте позволяет сделать настройку на определенный сигнал. Такую задачу решают с помощью колебательного контура.
Распределение спектра на экране измерительного прибора после обработки фильтром
Точно спроектированный фильтр будет «убирать» паразитные составляющие без дополнительных средств контроля и автоматизации. Такое решение, кроме простоты и минимальной стоимости, обеспечивает экономное потребление энергии генератором сигнала.
Как показано на практических примерах, резонанс может выполнять полезные и вредные функции. Точный расчет поможет создать качественную электрическую цепь с заданными техническими параметрами.
В чем заключается явление резонанса напряжений
Как известно, в сети переменного тока домашней сети разность потенциалов изменяется с частотой 50 Гц. То есть, каждую секунду производится 50 полных колебаний. Такое явление несложно замерить даже бытовым частотомером, который определить точное значение этого параметра именно по эффекту электромагнитного поля, образованного вокруг проводника с током. Катушка с металлическим сердечником, которая устанавливается в измерительный прибор, будет колебаться с частотой электромагнитного поля домашней электросети.
Вам это будет интересно Определение тока короткого замыкания
Частотомер
Таким образом, вырабатывается переменное напряжение, которое затем может быть увеличено, а его частота подсчитана микропроцессорным либо аналоговым устройством, после чего информация может быть выведена на экран.
Разобравшись, в чем заключается явление резонанса электрического напряжения, необходимо стараться всячески избегать этого явления, когда одновременные колебательные движения полей являются нежелательными. Если же в каком-либо устройстве такой эффект применяется с целью получения определенных физических явлений, то схема должна быть изготовлена с высокой добротностью, чтобы на поддержание процесса тратилось как можно меньше энергии (таким образом повышается КПД устройства).