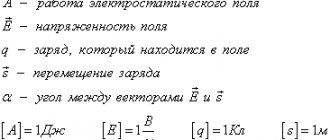Наверное, все мы сталкивались в детстве с чудесными свойствами обыкновенных магнитов. Небольшой кусок металла привлекал к себе одни кусочки железа и отталкивал другие.
Удивительные свойства магнита этим не ограничиваются. Например, магнит, подвешенный на нити, всегда располагается в пространстве определенным образом – это свойство легло в основу изобретения компаса. Конечные точки магнита являются наиболее «сильными». Их принято называть «полюсами». Специфические свойства магнита обусловлены его магнитными полями, которые не являются веществом, но ведут себя весьма осязаемо. Одной из самых важных характеристик является напряженность магнитного поля.
Характеристики магнитного поля
Любое магнитное поле обладает энергией, которая проявляет себя при взаимодействии с другими телами. Под влиянием магнитных сил движущиеся частички меняют направление своего потока. Магнитное поле появляется лишь вокруг тех электрических зарядов, которые находятся в движении. Всякое изменение электрического поля влечет за собой появление магнитных полей.
Обратное утверждение также верно: изменение магнитного поля — предпосылка к возникновению электрического. Такое тесное взаимодействие привело к созданию теории электромагнитных сил, с помощью которых и сегодня успешно объясняются различные физические явления.
Изображение магнитных полей
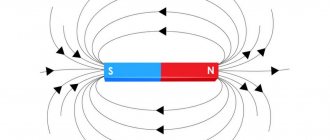
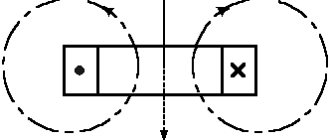
Магнитное поле можно изобразить на листе бумаги при помощи силовых линий. Их рисуют таким образом, чтобы реальное направление сил поля в каждой точке совпадало с нарисованными. Направления силовых полей могут быть определены при помощи компасной стрелки, северный полюс которой всегда направлен по касательной к силовой линии. Северный полюс принято обозначать местом, откуда выходят силовые линии магнитного поля, и южный – местом их вхождения. Следует помнить, что такое разделение весьма условно, и принимается во внимание только из-за своей наглядности.
Что такое магнитная напряженность
Железные опилки, выстраивающиеся вдоль магнитных полей, доказывают, что магнитное поле имеет два важных показателя – величину и направление. В любой точке пространства магнитное поле распространяется со скоростью, равной скорости света в вакууме — 300000 километров/сек.
Чтобы дать определение характеристикам магнитного поля, ученые ввели величину «напряженность». Это векторная величина, указывающая направление действия магнитного поля и на количество его силовых линий. По своим характеристикам напряженность магнитного поля аналогична понятию «силы» в механике. Этот показатель не зависит от параметров среды, в которой проводятся эксперименты, а только от силы магнитного потока и расстояния до источника, продуцирующего поле. В различных случаях таким источником может служить одиночный магнит, магнитная катушка, электрический провод. В каждом из этих случаев возникает магнитное поле с определенными характеристиками.
Магнитное поле в веществе. Напряжённость магнитного поля
Лекция 9. Магнитные свойства
Вещества
План лекции
9.1. Магнитный момент атома. Намагниченность вещества.
9.2. Магнитное поле в веществе. Напряжённость магнитного поля.
9.3. Виды магнетиков: диамагнетики, парамагнетики, ферромагнетики.
9.4. Свойства ферромагнетиков. Элементы теории ферромагнетизма. Применение ферромагнетиков.
Магнитный момент атома. Намагниченность вещества
Магнитное поле, создаваемое токами проводимости (макротоками) в среде, отличается от магнитного поля в вакууме. Это изменение связано со взаимодействием магнитного поля с веществом, в результате которого вещество намагничивается и приобретает магнитный момент. Причиной намагничивания является существование молекулярных токов. Ещё в 1820 году Ампер высказал гипотезу о существовании элементарных круговых токов в веществе. Природа элементарных токов стала понятна и гипотеза подтвердилась, когда было установлено, что атом состоит из ядра и движущихся вокруг электронов по модели атома Резерфорда.[1]
В классической физике электрон (е
), обращающийся вокруг ядра по орбите в радиуса
r
, с частотой
ν,
эквивалентен круговому току
J
и обладает орбитальным магнитным моментом
,
где — сила тока, — площадь орбиты, — единичная нормаль к плоскости орбиты.
Также движущийся по орбите электрон обладает механическим моментом импульса , называемым орбитальным, величина которого равна
Вектора и направлены противоположно и их отношение, равное
,
называется гиромагнитным отношением.
В 1915 году Эйнштейн[2] и де Гааз[3] установили, что экспериментальное значение гиромагнитного отношения в два раза больше и равно
.
Для объяснения полученного результата они предположили, что помимо орбитальных моментов, электрон обладает собственным механическим моментом импульса , названным спином, и собственным, спиновым магнитным моментом . Их отношение и равно . Это предположение впоследствии подтвердилось.
Таким образом, электрон в атоме обладает орбитальным магнитным моментом и спиновым магнитным моментом . Зная число электронов в атоме, их расположение и взаимодействие, можно определить магнитный момент атома.
В простейшем случае вычисляют в виде векторной суммы орбитальных и спиновых магнитных моментов электронов атома:
(Магнитным моментом ядра атома пренебрегают, ввиду его малости).
Благодаря магнитным моментам атомов любое вещество обладает магнитными свойствами и является магнетиком. Под действием магнитного поля магнетик намагничивается. Намагничивание вещества характеризует вектор , называемый намагниченностью вещества, и равный магнитному моменту единицы объёма магнетика:
,
где V –
физически малый объём.
Намагниченность характеризует магнитное состояние вещества. В системе СИ намагниченность измеряется в [I
]=1 А/м.
Магнитное поле в веществе. Напряжённость магнитного поля
Магнитное поле в веществе складывается из внешнего магнитного поля , созданного макротоками проводимости (магнитного поля, созданного макротоками в вакууме) и магнитного поля , возникающего благодаря намагничиванию вещества (за счет магнитных моментов атомов) и равно
.
Введем вспомогательную характеристику магнитного поля, которая определяется только макротоками и не зависит от микротоков вещества. Эту величину называют напряженностью магнитного поля и можно показать, что она равна
Преобразовав эту формулу, получим выражение полной магнитной индукции в веществе:
. (9.1)
В изотропных средах и слабых полях намагниченность пропорциональна напряженности , , где коэффициентом пропорциональности является безразмерная величина — магнитная восприимчивость вещества.
После подстановки в (9.1), получим:
, (9.2)
где — магнитная проницаемость вещества.
В изотропных, однородных средах, где вектора и параллельны, магнитная проницаемость показывает, во сколько раз изменяется магнитная индукция в магнетике по сравнению с магнитной индукцией в вакууме.
Теорема Остроградского1-Гаусса2 для магнитной индукции магнетика запишется:
. (9.3)
Поток вектора через любую замкнутую поверхность S
равен нулю.
Закон полного тока для магнитного поля в веществе имеет вид:
,
где J
и — алгебраические суммы сил макротоков
J
и макротоков .
Можно показать, что , тогда . Величина, стоящая в скобках , равна напряженности магнитного поля и:
. (9.4)
Циркуляция вектора напряжённости по замкнутому контуру равна алгебраической сумме сил токов проводимости J
(макротоков), охватываемых этим контуром.
Закон Био–Савара–Лапласа для магнитного поля в веществе имеет вид:
.
1
Напряженность электромагнитного поля в экспериментах
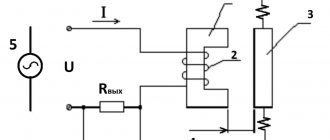
Рассмотрим одиночный провод, по которому движется электрический ток. При движении этого провода вокруг него возникает магнитное поле. Его характеристики можно выразить через напряженность, которая определяется мерой воздействия магнитного поля на исследуемое тело.
Можно исследовать магнитное поле внутри катушки. В этом случае напряженность будет напрямую зависеть от количества витков катушки и расстояния между нею и исследуемым телом.
Объединяя эти два вывода, можно подвести итоги: напряженность магнитного поля в любой точке пространства обратно пропорциональна длине магнитной линии и прямо пропорциональна произведению количества витков катушки на силу тока.
Циркуляция вектора напряженности магнитного поля
Существует теорема о циркуляции магнитного поля. Это одна из основных теорем электродинамики, сформулированная Анри Ампером. Ее также иногда называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля – своеобразный аналог теоремы Гаусса о циркуляции вектора напряженности электрического поля.
Теорема о циркуляции магнитного поля
Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости, охваченных контуром, по которому рассматривается циркуляция.
Определить циркуляцию вектора напряженности для замкнутого контура L .
I 1 = 5 A , I 2 = 2 A , I 3 = 10 A , I 4 = 1 A .
По теореме о циркуляции:
Рассматриваемый контур охватывает токи I 1 , I 2 , I 3 .
Подставим значения c учетом указанных на рисунке направлений токов и вычислим циркуляцию:
∮ H → d r → = ∑ I m = 5 A 12 A + 10 A = 13 A .
Магнитное поле – вихревое поле, которое не является потенциальным. Циркуляция вектора напряженности в общем случае отлична от нуля.
Для описания магнитного поля используются две его основные характеристики – индукция B → и напряженность H → . Эти величины связаны между собой. Рассмотрим, что такое напряженность магнитного поля, чему она равна, каков физический смысл этой величины.
Магнитная индукция
Определение напряженности магнитного поля было бы неполным без понятия «магнитная индукция». Эта величина объясняет, какую работу способно производить данное магнитное поле. Чем сильнее магнитное поле, тем больше работы оно может производить, тем больше значение его магнитной индукции.
В физике магнитная индукция обозначается литерой Ḇ. Наглядно ее можно изобразить в виде плотности магнитных силовых линий, приходящихся на единицу площади поверхности, которая расположена перперндикулярно к измеряемому магнитному полю. В настоящее время магнитная индукция измеряется в Теслах.
Циркуляция вектора напряженности магнитного поля
Существует теорема о циркуляции магнитного поля. Это одна из основных теорем электродинамики, сформулированная Анри Ампером. Ее также иногда называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля – своеобразный аналог теоремы Гаусса о циркуляции вектора напряженности электрического поля.
Теорема о циркуляции магнитного поля
Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости, охваченных контуром, по которому рассматривается циркуляция.
Определить циркуляцию вектора напряженности для замкнутого контура L .
I 1 = 5 A , I 2 = 2 A , I 3 = 10 A , I 4 = 1 A .
По теореме о циркуляции:
Рассматриваемый контур охватывает токи I 1 , I 2 , I 3 .
Подставим значения c учетом указанных на рисунке направлений токов и вычислим циркуляцию:
∮ H → d r → = ∑ I m = 5 A 12 A + 10 A = 13 A .
Магнитное поле – вихревое поле, которое не является потенциальным. Циркуляция вектора напряженности в общем случае отлична от нуля.
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
- 5
- 4
- 3
- 2
- 1
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Магнитный поток
Еще одна величина, емко характеризующая магнитное поле. Магнитный поток определяет, какое количество силовых линий пронизывает определенную единицу площади. В однородном магнитном поле значение магнитного потока будет вычислено по формуле:
Ф= Ḇ/S, где:
Ф — магнитный поток;
Ḇ — значение магнитной индукции;
S – площадь, через которую проходя силовые линии магнитного поля.
В системе единиц СИ магнитный поток измеряется в Веберах.
Базовые формулы
Здесь изложены основные формулы теории магнетизма. Информация для школьников, студентов и всех кого интересует этот вопрос
Правило правой руки или буравчика:
Направление силовых линий магнитного поля и направление создающего его тока связаны между собой известным правилом правой руки или буравчика, которые ввел еще Д.Максвелл и иллюстрируется следующими рисунками:
Мало кто знает, что буравчик — это инструмент для бурения-сверления отверстий в дереве. Поэтому более понятно можно это правило назвать правилом винта, шурупа или штопора. Однако хвататься за провод как на рисунке иногда опасно для жизни!
Магнитная индукция B :
Магнитная индукция — является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряженности электрического поля E . Вектор магнитной индукции всегда направлен по касательной к магнитной линии и показывает ее направление и силу. За единицу магнитной индукции в B = 1Тл принимается магнитная индукция однородного поля, в котором на участок проводника длиной в l = 1 м, при силе тока в нем в I = 1 А, действует со стороны поля максимальная сила Ампера — F = 1 H. Направление силы Ампера определяется по правилу левой руки . В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл).
Напряженность магнитного поля H :
Еще одной характеристикой магнитного поля является напряженность, которая является аналогом вектора электрического смещения D в электростатике. Определяется по формуле:
Напряженность магнитного поля — величина векторная, является количественной характеристикой магнитного поля и не зависит от магнитных свойств среды. В системе СГС напряженность магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м).
Магнитный поток Ф:
Магнитный поток Ф — скалярная физическая величина, характеризующая число линий магнитной индукции, пронизывающих замкнутый контур. Рассмотрим частный случай. В однородном магнитном поле , модуль вектора индукции которого равен ∣ В ∣, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол α с направлением вектора магнитной индукции B . Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:
В общем случае магнитный поток определяется как интеграл вектора магнитной индукции B через конечную поверхность S.
Стоит отметить, что магнитный поток через любую замкнутую поверхность равен нулю (теорема Гаусса для магнитных полей). Это означает, что силовые линии магнитного поля нигде не обрываются т.е. магнитное поле имеет вихревую природу, а также что невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле. В СИ единицей магнитного потока является Вебер (Вб), в системе СГС — максвелл (Мкс); 1 Вб = 10 8 Мкс.