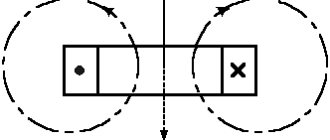
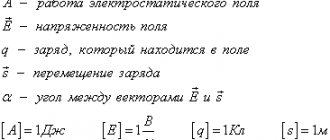Probably, we all encountered in childhood the wonderful properties of ordinary magnets. A small piece of metal attracted some pieces of iron and repelled others.
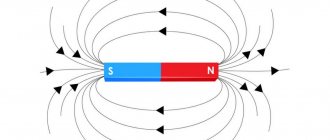
The amazing properties of a magnet don’t stop there. For example, a magnet suspended on a thread is always located in space in a certain way - this property formed the basis for the invention of the compass. The end points of the magnet are the "strongest". They are usually called “poles”. The specific properties of a magnet are due to its magnetic fields, which are not matter, but behave in a very tangible way. One of the most important characteristics is the magnetic field strength.
Characteristics of the magnetic field
Any magnetic field has energy that manifests itself when interacting with other bodies. Under the influence of magnetic forces, moving particles change the direction of their flow. A magnetic field appears only around those electric charges that are in motion. Any change in the electric field entails the appearance of magnetic fields.
The opposite statement is also true: a change in the magnetic field is a prerequisite for the emergence of an electric one. Such close interaction led to the creation of the theory of electromagnetic forces, with the help of which various physical phenomena are successfully explained today.
Image of magnetic fields
A magnetic field can be depicted on a sheet of paper using lines of force. They are drawn in such a way that the real direction of the field forces at each point coincides with those drawn. The directions of force fields can be determined using a compass needle, the north pole of which is always tangent to the field line. The North Pole is usually designated as the place from which magnetic field lines emerge, and the South Pole as the place where they enter. It should be remembered that such a division is very arbitrary and is taken into account only because of its clarity.
What is magnetic intensity
Iron filings lining up along magnetic fields prove that a magnetic field has two important parameters - magnitude and direction. At any point in space, the magnetic field propagates at a speed equal to the speed of light in a vacuum - 300,000 kilometers/sec.
To define the characteristics of the magnetic field, scientists introduced the value of “tension”. This is a vector quantity indicating the direction of action of the magnetic field and the number of its lines of force. In its characteristics, magnetic field strength is similar to the concept of “force” in mechanics. This indicator does not depend on the parameters of the environment in which the experiments are carried out, but only on the strength of the magnetic flux and the distance to the source producing the field. In various cases, such a source can be a single magnet, a magnetic coil, or an electric wire. In each of these cases, a magnetic field with certain characteristics arises.
Magnetic field in matter. Magnetic field strength
Lecture 9. Magnetic properties
Substances
Lecture outline
9.1. Magnetic moment of an atom. Magnetization of a substance.
9.2. Magnetic field in matter. Magnetic field strength.
9.3. Types of magnets: diamagnetic, paramagnetic, ferromagnetic.
9.4. Properties of ferromagnets. Elements of the theory of ferromagnetism. Application of ferromagnets.
Magnetic moment of an atom. Magnetization of a substance
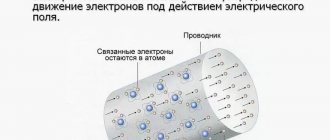
The magnetic field created by conduction currents (macrocurrents) in a medium differs from the magnetic field in a vacuum. This change is associated with the interaction of a magnetic field with a substance, as a result of which the substance is magnetized and acquires a magnetic moment. The reason for magnetization is the existence of molecular currents. Back in 1820, Ampere put forward a hypothesis about the existence of elementary circular currents in matter. The nature of elementary currents became clear and the hypothesis was confirmed when it was established that the atom consists of a nucleus and electrons moving around according to the Rutherford atomic model.[1]
In classical physics, the electron ( e
), revolving around the nucleus in an orbit of radius
r
, with a frequency
ν,
is equivalent to a circular current
J
and has an orbital magnetic moment
,
where is the current strength, is the orbital area, and is the unit normal to the orbital plane.
Also, an electron moving in an orbit has a mechanical angular momentum, called orbital, the value of which is equal to
The vectors and are oppositely directed and their ratio is equal
,
called the gyromagnetic ratio.
In 1915, Einstein[2] and de Haas[3] established that the experimental value of the gyromagnetic ratio is twice as large and equal to
.
To explain the result, they suggested that in addition to orbital moments, the electron has its own mechanical angular momentum, called spin, and its own spin magnetic moment. Their ratio is equal. This assumption was later confirmed.
Thus, an electron in an atom has an orbital magnetic moment and a spin magnetic moment. Knowing the number of electrons in an atom, their location and interaction, we can determine the magnetic moment of the atom.
In the simplest case, it is calculated as a vector sum of the orbital and spin magnetic moments of the electrons of an atom:
(The magnetic moment of the atomic nucleus is neglected due to its smallness).
Thanks to the magnetic moments of atoms, any substance has magnetic properties and is magnetic. Under the influence of a magnetic field, a magnet becomes magnetized. The magnetization of a substance is characterized by a vector called the magnetization of the substance, which is equal to the magnetic moment of a unit volume of the magnet:
,
where V –
physically small volume.
Magnetization characterizes the magnetic state of a substance. In the SI system, magnetization is measured in [ I
]=1 A/m.
Magnetic field in matter. Magnetic field strength
The magnetic field in a substance consists of an external magnetic field created by conduction macrocurrents (magnetic field created by macrocurrents in a vacuum) and a magnetic field arising due to the magnetization of the substance (due to the magnetic moments of atoms) and is equal to
.
Let us introduce an auxiliary characteristic of the magnetic field, which is determined only by macrocurrents and does not depend on the microcurrents of the substance. This quantity is called the magnetic field strength and can be shown to be equal to
Transforming this formula, we obtain the expression for the total magnetic induction in a substance:
. (9.1)
In isotropic media and weak fields, magnetization is proportional to the intensity, , where the proportionality coefficient is a dimensionless quantity—the magnetic susceptibility of the substance.
After substitution into (9.1), we get:
, (9.2)
where is the magnetic permeability of the substance.
In isotropic, homogeneous media, where the vectors and are parallel, magnetic permeability shows how many times the magnetic induction in a magnet changes compared to the magnetic induction in a vacuum.
The Ostrogradsky1-Gauss2 theorem for the magnetic induction of a magnet will be written:
. (9.3)
Vector flow through any closed surface S
equal to zero.
The total current law for a magnetic field in a substance has the form:
,
where J
and are the algebraic sums of the forces of macrocurrents
J
and macrocurrents .
It can be shown that , then . The value in parentheses is equal to the magnetic field strength and:
. (9.4)
The circulation of the tension vector along a closed loop is equal to the algebraic sum of the strengths of the conduction currents J
(macrocurrents) covered by this circuit.
The Biot-Savart-Laplace law for the magnetic field in matter has the form:
.
1
Electromagnetic field strength in experiments
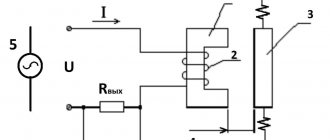
Consider a single wire carrying an electric current. When this wire moves, a magnetic field is created around it. Its characteristics can be expressed through intensity, which is determined by the measure of the influence of the magnetic field on the body under study.
You can examine the magnetic field inside the coil. In this case, the voltage will directly depend on the number of turns of the coil and the distance between it and the body under study.
Combining these two conclusions, we can summarize: the magnetic field strength at any point in space is inversely proportional to the length of the magnetic line and directly proportional to the product of the number of turns of the coil and the current strength.
Circulation of the magnetic field strength vector
There is a theorem about the circulation of the magnetic field. This is one of the fundamental theorems of electrodynamics, formulated by Henri Ampère. It is also sometimes called Ampere's theorem or law. The theorem on the circulation of the magnetic field is a kind of analogue of the Gauss theorem on the circulation of the electric field strength vector.
Magnetic field circulation theorem
The circulation of the magnetic field strength vector along a closed loop is equal to the algebraic sum of the conduction currents covered by the loop along which the circulation is considered.
Determine the circulation of the tension vector for a closed loop L.
I 1 = 5 A, I 2 = 2 A, I 3 = 10 A, I 4 = 1 A.
According to the circulation theorem:
The circuit under consideration covers the currents I 1, I 2, I 3.
Let's substitute the values taking into account the current directions indicated in the figure and calculate the circulation:
∮ H → dr → = ∑ I m = 5 A 12 A + 10 A = 13 A .
A magnetic field is a vortex field that is not potential. The circulation of the tension vector is generally different from zero.
To describe the magnetic field, two of its main characteristics are used - induction B → and intensity H →. These quantities are related to each other. Let's consider what magnetic field strength is, what it is equal to, and what the physical meaning of this quantity is.
Magnetic induction
The definition of magnetic field strength would be incomplete without the concept of “magnetic induction”. This value explains how much work a given magnetic field can produce. The stronger the magnetic field, the more work it can produce, the greater the value of its magnetic induction.
In physics, magnetic induction is denoted by the letter Ḇ. It can be visually depicted as the density of magnetic field lines per unit surface area, which is located perpendicular to the measured magnetic field. Currently, magnetic induction is measured in Tesla.
Circulation of the magnetic field strength vector
There is a theorem about the circulation of the magnetic field. This is one of the fundamental theorems of electrodynamics, formulated by Henri Ampère. It is also sometimes called Ampere's theorem or law. The theorem on the circulation of the magnetic field is a kind of analogue of the Gauss theorem on the circulation of the electric field strength vector.
Magnetic field circulation theorem
The circulation of the magnetic field strength vector along a closed loop is equal to the algebraic sum of the conduction currents covered by the loop along which the circulation is considered.
Determine the circulation of the tension vector for a closed loop L.
I 1 = 5 A, I 2 = 2 A, I 3 = 10 A, I 4 = 1 A.
According to the circulation theorem:
The circuit under consideration covers the currents I 1, I 2, I 3.
Let's substitute the values taking into account the current directions indicated in the figure and calculate the circulation:
∮ H → dr → = ∑ I m = 5 A 12 A + 10 A = 13 A .
A magnetic field is a vortex field that is not potential. The circulation of the tension vector is generally different from zero.
- Author: Maria Sukhorukikh
Rate this article:
- 5
- 4
- 3
- 2
- 1
(0 votes, average: 0 out of 5)
Share with your friends!
Magnetic flux
Another quantity that capaciously characterizes the magnetic field. Magnetic flux determines how many lines of force penetrate a certain unit of area. In a uniform magnetic field, the value of the magnetic flux will be calculated by the formula:
Ф= Ḇ/S, where:
F—magnetic flux;
Ḇ—magnetic induction value;
S is the area through which the magnetic field lines pass.
In SI units, magnetic flux is measured in Webers.
Basic formulas
Here are the basic formulas of the theory of magnetism. Information for schoolchildren, students and anyone interested in this issue
Right hand or gimlet rule:
The direction of the magnetic field lines and the direction of the current creating it are interconnected by the well-known rule of the right hand or gimlet, which was introduced by D. Maxwell and is illustrated by the following drawings:
Few people know that a gimlet is a tool for drilling holes in wood. Therefore, it is more understandable to call this rule the rule of a screw, screw or corkscrew. However, grabbing the wire as in the picture is sometimes life-threatening!
Magnetic induction B:
Magnetic induction is the main fundamental characteristic of a magnetic field, similar to the electric field strength vector E. The magnetic induction vector is always directed tangentially to the magnetic line and shows its direction and strength. The unit of magnetic induction in B = 1 T is taken to be the magnetic induction of a uniform field in which a section of conductor length l = 1 m, with a current strength in it of I = 1 A, is acted on by the field from the maximum Ampere force - F = 1 H. The direction of the Ampere force is determined by the left-hand rule. In the CGS system, magnetic field induction is measured in gauss (G), in the SI system - in tesla (T).
Magnetic field strength H:
Another characteristic of a magnetic field is intensity , which is an analogue of the electric displacement vector D in electrostatics. Determined by the formula:
Magnetic field strength is a vector quantity, is a quantitative characteristic of the magnetic field and does not depend on the magnetic properties of the medium. In the CGS system, magnetic field strength is measured in oersteds (Oe), in the SI system - in amperes per meter (A/m).
Magnetic flux F:
Magnetic flux Ф is a scalar physical quantity that characterizes the number of magnetic induction lines penetrating a closed loop. Let's consider a special case. In a uniform magnetic field, the magnitude of the induction vector is equal to ∣ B ∣, a flat closed circuit of area S is placed. The normal n to the plane of the circuit makes an angle α with the direction of the magnetic induction vector B. The magnetic flux through the surface is the quantity Ф, determined by the relation:
In general, magnetic flux is defined as the integral of the magnetic induction vector B through a finite surface S.
It is worth noting that the magnetic flux through any closed surface is zero (Gauss's theorem for magnetic fields). This means that the magnetic field lines do not break off anywhere, i.e. the magnetic field has a vortex nature, and also that it is impossible for the existence of magnetic charges that would create a magnetic field in the same way that electric charges create an electric field. In the SI, the unit of magnetic flux is Weber (Wb), in the CGS system it is Maxwell (Mx); 1 Wb = 10 8 μs.