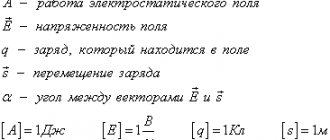Electric field potential is a scalar quantity of a body that characterizes intensity. Electrical power is expressed through a certain parameter. An important property of the electric field, which does not contain vortices and is formed by immovable sources, is its potential. Scientists spent a long time thinking about the characteristics of electric and magnetic fields until their essence became fully clear.
Real value of electric field
Scientists have been studying the secret of electricity for a long time. The main award for her research goes to Ørsted. His main discovery was the first experimental establishment of a connection between electrical and magnetic phenomena in 1819-1820.
It became clear that the oscillations involve a superposition of time-varying electric and magnetic fields. The magnetic intensity vector is perpendicular to the electric vector connected through a long medium (some physical quantity). Electrostatic action is action through a field.
Features of the impact:
- Each electric charge creates an electrostatic field around itself.
- An electric field is a space in which tension forces act.
- The quantities characterizing the field at this point are intensity and potential.
The intensity of the electrostatic phenomenon at this point is the ratio of the electric force acting on a test charge (positive) placed at this point to the value of this charge:
- E =F /q (over E and F vector).
- The unit of electrostatic field strength is 1 N/C.
The electric field strength at this point always has a rebound in accordance with the direction of the force acting on the positive test charge.
The value of the electrostatic field strength at a distance R from the source Q can be denoted by a simple formula: E=k |Q|/R2.
To graphically represent the field, lines are used - curves for which the intensity vector at each point has a tangent part. A field with spherical symmetry is called central. If the lines are parallel to each other, and the intensity has the same value at each point, then the field is called uniform.
The potential difference in physics at a given moment is the ratio of the energy of a point positive test load placed at this point to the value of this charge: V=Ep/q.
The unit of electric field point potential is 1 V (volt).
The electric field potential, formula at a distance R from the source Q can be calculated: V=k Q/r.
Measuring voltage with an oscilloscope
An illustration of the above will be a series of experiments on measuring voltages using a signal generator, a constant voltage source, an oscilloscope and a multifunctional digital instrument (multimeter).
Experiment No. 1
The general scheme of experiment No. 1 is presented below:
The signal generator is loaded onto a load resistance R1 of 1 kOhm, and the measuring ends of an oscilloscope and a multimeter are connected in parallel to the resistance. When conducting experiments, we take into account the fact that the operating frequency of the oscilloscope is significantly higher than the operating frequency of the multimeter.
Experience 1:
Let us apply a sinusoidal signal from the generator with a frequency of 60 hertz and an amplitude of 4 volts to the load resistance. On the oscilloscope screen we will observe the image shown below. Note that the cost of dividing the scale grid of the oscilloscope screen along the vertical axis is 2 V. The multimeter and oscilloscope will show an rms voltage value of 1.36 V.
Experience 2:
Let's double the signal from the generator, the scope of the image on the oscilloscope will double exactly and the multimeter will show double the voltage value:
Experience 3:
Let's increase the generator frequency by 100 times (6 kHz), and the frequency of the signal on the oscilloscope will change, but the peak-to-peak and root-mean-square value will remain the same, and the multimeter readings will become incorrect - the permissible operating frequency range of the multimeter is affected: 0-400 Hz:
Experience 4:
Let's return to the original frequency of 60 Hz and the voltage of the signal generator 4 V, but change the shape of its signal from sine to triangular. The scope of the image on the oscilloscope remained the same, but the multimeter readings decreased compared to the voltage value that it showed in experiment No. 1, since the effective signal voltage changed:
Experiment No. 2
The design of experiment No. 2 is similar to the design of experiment 1.
Using the knob for changing the bias voltage on the signal generator, we will add a bias of 1 V. On the signal generator, we will set a sinusoidal voltage with a swing of 4 V with a frequency of 60 Hz - as in experiment No. 1. The signal on the oscilloscope will rise by half a major division, and the multimeter will show an rms value of 1.33 V. The oscilloscope will show an image similar to the image from experiment 1 of experiment #1, but raised by half a major division. A multimeter will show almost the same voltage as it was in experiment 1 of experiment No. 1, since it has a closed input, and an oscilloscope with an open input will show an increased effective value of the sum of direct and alternating voltages, which is greater than the effective value of the voltage without a constant component:
Charge around an object
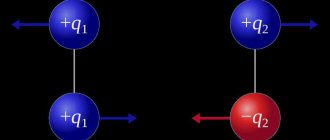
Of course, we can talk about the field if there is any source of it. Each electric body creates a gradient of electric field potential around itself. Compared to gravitational fields, there is an important difference:
- Gravitational forces are forces of attraction and can be measured.
- The forces of electricity can be either attractive or repulsive.
It is known that field lines refer to the force vectors acting on the body at this point. Scientists agreed that the arrows of the field line will exhibit the reverse vector of the force acting on the negative charge. Consequently, the lines of force “leave” from positive charges and “run” towards negative energy charges.
Electric field strength
In an electric field, as well as in a gravitational field, the concept of tension arises. This indicates what force will act, and it is known that this force depends on the source and the distance. It is the intensity that is the characteristic of this field, which can be charged. By definition, electric field strength is the ratio of the force acting on its value.
If the field is not caused by one source, but, for example, by two positive charges, then to calculate the intensity at this point in space it makes sense to apply the principle of superposition.
For example, there is central field data created by charge Q. A test charge q should be placed at a distance R1. The work is done to move this test charge to a distance R2 from the field source.
In order for the charge system to move at the same speed, it is necessary to constantly act on it with a force that balances the Coulomb value. But along with a change in the distance from the source, this force changes in inverse proportion to the square of the distance. You need to use the average value acting on the test charge.
To determine whether work is positive or negative, you need to think about the angle between the applied force vector and the displacement vector . If the test charge is attracted by the source of the field, and the work done moves that charge closer to the source, then the attraction needs to be balanced.
In a word, they apply a force that creates a displacement of 180° with the vector. If cos (α)= -1, then the work is negative. But if the source interacts with the load in such a way as to balance the force parallel to the displacement chain, so that the condition α = 0°, i.e. cos (α) = 1, the work is positive.
Electrostatic field potential and potential difference
In mechanics, the mutual action of bodies on each other is characterized by force or potential energy. The electrostatic field that carries out the interaction between charges is also characterized by two quantities. Field strength is a force characteristic. Now let’s introduce an energy characteristic—potential.
Field potential . The work of any electrostatic field when moving a charged body in it from one point to another also does not depend on the shape of the trajectory, just like the work of a uniform field. On a closed trajectory, the work of the electrostatic field is always zero. Fields with this property are called potential. In particular, the electrostatic field of a point charge has a potential character.
The work of a potential field can be expressed in terms of a change in potential energy. The formula A= - (WP1 - WP2) is valid for any electrostatic field. And only in the case of a uniform field, the potential energy is expressed by the formula Wp=qEd.
Potential
The potential energy of a charge in an electrostatic field is proportional to the charge. This is true both for a uniform field and for any other. Therefore, the ratio of potential energy to charge does not depend on the charge placed in the field.
This allows us to introduce a new quantitative characteristic of the field - potential, which does not depend on the charge placed in the field.
The electrostatic field potential is the ratio of the potential energy of a charge in the field to this charge.
According to this definition, the potential is equal to:
(1)
The field strength is a vector and represents the strength characteristic of the field; it determines the force acting on the charge q at a given point in the field. Potential φ is a scalar, it is an energy characteristic of the field; it determines the potential energy of the charge q at a given point in the field.
If we take a negatively charged plate as the zero level of potential energy, and therefore potential, then according to formulas Wp=qEd and (1) the potential of a uniform field is equal to:
(1)
Potential difference
Like potential energy, the value of the potential at a given point depends on the choice of the zero level for reading the potential. What is of practical importance is not the potential itself at a point, but the change in potential, which does not depend on the choice of the zero level of the potential reference.
Since potential energy Wp = qφ, the work is equal to:
(2)
Here
(3)
potential difference, i.e. the difference in potential values at the initial and final points of the trajectory.
Potential difference is also called voltage.
According to formulas (2) and (3), the potential difference is equal to:
(4)
The potential difference (voltage) between two points is equal to the ratio of the work done by the field when moving a charge from the starting point to the final point to this charge.
Knowing the voltage in the lighting network, we thereby know the work that an electric field can do when moving a unit charge from one socket contact to another along any electrical circuit. We will deal with the concept of potential difference throughout the entire physics course.
Unit of potential difference
The unit of potential difference is set using formula (4). In the International System of Units, work is expressed in joules and charge in coulombs. Therefore, the potential difference between two points is equal to one if, when moving a charge of 1 C from one point to another, the electric field does 1 J of work. This unit is called a volt (V); 1 V = 1 J/1 C.
The energy characteristic of an electrostatic field is called potential. The potential is equal to the ratio of the potential energy of the charge in the field to the charge. The potential difference between two points is equal to the work done to move a unit charge.
Potential energy
When calculating the potential energy of a test charge at this point in the field, they use the property in which the difference in potential energy at two points is equal to the work done when moving this value from one point to another (the same was done, including the energy in the gravitational field).
In order to calculate the potential energy at this point, you need to move the test charge to a place where the potential is zero. Such a place is located at a point infinitely distant from the source. The positive or negative sign of the potential is chosen depending on whether the load with the source repels or attracts. If the source charge is negative, then finding the electrostatic potential is the same. When the source is positive, so is the potential.
Equipotential surfaces
If we assume that the source of the electric field is a pointwise charged particle (i.e., a central field), it follows that all points in space that are equally far from it have equal potential. In space, a collection of such points forms the surface of a sphere, and the source charge is located in the center of the sphere.
However, if the electric field is not centralized, it is still possible to assign surfaces such that a test charge placed at any point on this surface will have the same potential. For example, in the case of a uniform field, such a surface is any plane perpendicular to the field line.
Topic 3. Field potentials of various charged bodies.
1. Electron with initial energy W
moves from afar in a vacuum towards the center of a uniformly charged ball of radius
R.
Assuming the charge of the ball to be negative and equal to
q,
find the minimum distance r at which the electron will approach the surface of the ball.
2. Find what the work is when transferring a point charge of 20 nC from infinity to a point located at a distance of 1 cm from the surface of a ball of radius 1 cm, charged with a surface charge density of 1 nC/cm2.
3. Find the work (per unit length) that needs to be done to bring two similarly charged long parallel threads closer together from a distance of 20 cm to 10 cm between them. The linear charge density of each thread is 3 µC/m. In 0.5 = - 0.69.
4. A thin straight long thread is uniformly charged with a linear charge density of 2 µC/m. Find the filament field potential as a function of distance r
from the thread.
Calculate the potential at a distance of 10 m, taking φ
=
0
at a distance of 1 m.
5. At opposite vertices of a square with side a
two point charges (+q) and (-
2q) are placed.
Find the field potential at each of the unoccupied vertices of the square.
6. A thin rod is bent into a ring of radius R,
uniformly charged with linear density
m.
Find the field potential at a point located on the axis of the ring at a distance
x
from its center.
7. Charge q
uniformly distributed over a semiring of radius R. Find the potential at the center of the semiring.
8. Ring of radius R
made of thin wire has a charge
q.
Find the electric field potential at the center of the ring, assuming that
φ=
0.
10 The electric field is created by two infinite parallel planes charged with surface densities of 1 nC/m2 and 5 nC/m2. Find the potential difference between the planes if the distance between them is 5 mm.
11 Sphere of radius R
uniformly charged with surface charge density a.
Find the electric field potential on the surface of the sphere, inside and outside it. Plot a graph of φ(r).
12. Find the potential at the center of a metal sphere of radius R,
charged uniformly with surface charge density σ.
13. Obtain an expression for the potential φ
fields of a flat capacitor depending on the
x
directed perpendicular to the capacitor plates.
Draw graphs of the dependence φ (x),
taking
φ =
0: 1) on the first plate, 2) on the second plate and 3) in the plane lying midway between the plates.
14 A thin rod is bent into a half ring and charged with a linear charge density of 133 nC/m. Find the work that must be done to transfer a charge of 6.7 nC from the center of curvature of the semiring to infinity.
15.Ring of radius R
charged with linear charge density τ.
Find the work done by the field forces to move the charge q
from the center of the ring to a point located on the axis of the ring at a distance of 3
R
from its center.
16.An electron moves along the electric field line of a negatively charged extended plane. Find the minimum distance to which it can approach the plane if at a distance of 5 cm from the plane the kinetic energy of the electron is 8 kJ and the surface charge density of the plane is 35.4 C/m².
17.Two identical spheres of radius R
charged with charges
+q
and
-q.
Find the field strength and potential at the point lying in the middle of the straight line connecting the centers of the spheres, if the distance between the centers is 10R.
NC. Thin disk of radius R
uniformly charged with surface charge density
σ.
Find the field potential at the center of the disk.
19. Find the potentials in point A
and C, assuming that the potential at point
B
is 0.
All points lie on the same field line of a uniform electric field with a strength of 100 V/m.
a =1
seeDraw a graph of
φ(x).
20. Three plates are located in a vacuum parallel to each other. Distance from the middle plate to the outer ones d
and
2d.
σ
is uniformly distributed , on the second - (- 2
σ
), on the third - (- 3
σ
). Find the potential difference between plates 1 and 2,1 and 3,2 and 3.
21. An electric field is created by a long cylinder of radius 1 cm, uniformly charged with
linear charge density 20 mC/m. Find the potential difference between two points of this field located at distances of 0.5 cm and 2 cm from the cylinder axis in its middle part.