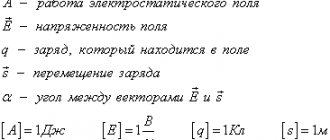Formulas for direct electric current
A direct electric current does not change in magnitude or direction. It is used to calculate a closed, homogeneous circuit, power and other parameters. Therefore, it is important to know the formulas for it and the basic laws associated with it.
You may be interested in Description and use of neodymium magnet
Basic list of formulas
Ohm's law for a section of a homogeneous chain
For electric current to exist, a field is needed. For its formation, potentials or their difference, expressed by voltage, are needed. The current will be directed towards reducing the potentials, and the electrons will begin to move in the opposite direction. In 1826, G. Ohm conducted a study and concluded: the higher the voltage, the greater the current that passes through the section.
For your information! Adjacent conductors conduct electricity differently. That is, each element has its own conductivity, electrical resistance.
As a result, according to Ohm’s theorem, the current strength for a section of a homogeneous circuit will be directly proportional to the voltage across it and inversely proportional to the conductive resistance.
Ohm's law
Using the formula I = U / R, where I is considered to be the current strength, U is the voltage, and R is the electrical resistance, the latter value can be found if p * l / S, where p is the conductor resistivity, l is the length of the conductor, and S — cross-sectional area of the conductor.
Ohm's law for a closed circuit with a current source
Ohm made a formula for a closed circuit. According to it, the current in this section from a current source having internal and external load resistance is equal to dividing the electromotive force of the source by the sum of the internal and external resistance. It looks like this: I = e / R + r, where I is the current force, e is the emf, R is the resistance, and r is the internal resistance of the voltage source.
Note! In the physical sense, according to this law, the higher the EMF, the higher the source of energy, the greater the speed of movement of charges. The higher the resistance, the lower the current.
Ohm's law for a closed circuit
DC operation
Energy, when passed through a conductor, moves in an orderly manner into the carrier. While moving, it does work. As a result, direct current work is the field activity aimed at transferring electrical charges along a conductor. It is equal to I multiplied by the voltage and time performed by the work.
Joule-Lenz law
When electricity passes through any resistive conductor, heat is always released. The amount of heat released over a certain period of time is determined by the Joule-Lenz law. According to the formula, the heat power is equal to the electricity density multiplied by the voltage - w =j * E = oE(2).
Note! In practical terms, the law is important for reducing electricity loss, selecting a conductor for an electrical circuit, selecting an electric heating device and using a fuse to protect the network.
Joule-Lenz law
Apparent power developed by the current source
Power is work done in one second of time. Electrical power is a physical quantity that characterizes the speed of transmission with the conversion of electricity.
The work that is developed by the source of electricity throughout the circuit is total power. It can be determined by the formula P = El, where E is considered the emf, and I is the value of the current characteristic.
For your information! If there is a linear load, then the total power indicator is equal to the square root of the squares of the active and reactive work of the source. If there is a nonlinear load, then it is equal to the square root of the squares of the active and inactive work of the source.
Full power
In practical measurements, such work is expressed in kilowatts per hour. Used to measure electricity consumption in domestic and industrial environments, to determine the generated electrical energy in electrical equipment.
Net power
The maximum or useful power is that which is released in the external gap of the circuit, that is, during the load of the resistor. It can be used to perform any tasks. A similar concept can be applied to calculate how an electric motor or transformer works, which is capable of consuming active and reactive components.
You may be interested in this. What is the unit of measurement for current?
Net power
The useful power indicator can be calculated using three formulas: P = I 2R, P = U2 / r, P = IU, where I is the current strength in a certain section of the circuit; U is the voltage on part of the terminals (clamps) of the current source, and R is the load resistance or external circuit.
Current source efficiency
The efficiency of a current source is the division of the useful power indicator by the total. If the internal resistance of the source is equal to the external resistance, then half the results of all the work will be lost in the source, and the other half will be allocated to the load. In such a situation, the efficiency will be 50%.
If we consider this concept most fully, then when electric charges move along a closed electrical circuit, the current source performs a certain useful and complete work. By performing the first, it moves charges into the external circuit. Doing the second work, charged particles move throughout the area.
Current source efficiency
Note! A useful effect is achieved when the resistance of the external electrical circuit has a certain value, depending on the source and load. The ratio of useful work to full is expressed by the formula: η = Apolez / Apoln = Ppolez / Pfull = U/ε = R / (R + r).
Kirchhoff's first rule
According to Kirchhoff's first law, the current sum in any part of the electrical circuit is equal to zero. The directional charge towards the node is positive, and from it - negative. The algebraic current sum of charges that are directed towards a node is equal to the sum of those that are directed away from it. If we translate this rule, we can get the following definition: as much current enters the node, so much comes out of it. This rule follows from the law on the conservation of charged particles.
By solving linear equations based on Kirchhoff's rules, it is possible to find all current values and voltages in areas of direct, alternating and quasi-stationary electric currents.
Note! In electrical engineering, Kirchhoff's rule is of particular importance, since it is universal for solving many problems in the theory of electrical circuits. It can be used to calculate complex electrical circuits. Using it, you can obtain a system of linear equations for currents or voltages on all internodal branches of the circuits.
Kirchhoff's first rule
Kirchhoff's second rule
The second Kirchhoff rule follows from the first and third Maxwellian equations. According to it, the algebraic sum of the voltages on the resistive elements of a closed section is equal to the sum of the emf that is included in it. If there is no EMF in the area, then the total voltage drop is equal to zero. To put it even more simply, during a complete bypass of the circuit, the potential changes. It returns to its original value.
A common case for a section of one circuit is Ohm's law. When composing stress equations for a circuit, it is necessary to select its positive bypass. To do this, you need to know that when selecting a bypass, the branch voltage drop indicator will be positive if the bypass direction in the branch coincides with the one that was previously selected. If it does not match, then the branch voltage indicator will be negative.
Important! Kirchhoff's second rule can be used in a linear or nonlinear linearized circuit for any change in currents and voltages.
Kirchhoff's second rule
As a result, in order to understand the basics of physics, electrical phenomena, electrodynamics and successfully use knowledge in the process of life, you need to know the derived theorems, laws, formulas and rules in the field of electricity, which are presented above. For example, by imagining what this or that formula looks like, you can solve any problem in a textbook on physics or life.
Basic formulas of electricity
Studying the fundamentals of electrodynamics and electrics is impossible without determining the electric field, precise charges, resistance and other phenomena.
Electricity formulas
Therefore, it is important to consider all the basic formulas of electricity and examples of solving problems using them.
Coulomb's law
According to a short description, this is a physical law that talks about the interaction between directly standing point electric charges, depending on the distance at which they are located. According to the full definition, the formulation means that a vacuum is formed between two points in the form of electric charges. A specific force appears there, which is proportional to the multiplication of their modular particles divided by the square of the distance.
Distance is the length that connects charges. The interaction force is directed along the segment. Coulomb force is a force that is repulsive for charges minus-minus and plus-plus and attractive for charges minus-plus and plus-minus.
Note! The electric force formula looks like this: F=k⋅|q1|⋅|q2|/r2, where F is the force of the charge, q is the magnitude of the charge, r is the vector or distance between charges, and k is the proportionality coefficient. The latter is equal to c2·10−7 H/m.
Coulomb's law
Solving the problem with Coulomb's law. If you have charged balls that are located at a distance of 15 cm and repel with a force of 1 N in search of the initial charge, you can identify the unknown by converting the base units to the SI system and substituting the values into the indicated formula. The value will be 2 * 5 * 10 (-8) = 10 (-7).
Field strength of a solitary point charge
The electric field, being matter created by electric point charges, is characterized by different quantities, including intensity. Tension acts as a vector quantity or force characteristic of the field, which is directed towards the electrostatic interaction of charges. To obtain it, you need to use the formula E = k (q / r (2)), where E is a vector field.
Field strength of a solitary point charge
According to this formulation, the charge field strength is inversely proportional to the square value of the distance from the charge. That is, if the gap increases several times, the voltage indicator decreases by four.
You can apply the law to solve problems. For example, the radius is unknown. Then you need to convert the constant. You need to solve the equation E / r (2) = kq by substituting known numbers.
Potential of a point in the field of a point charge
Potential in an electrostatic field is a scalar quantity that is equal to dividing the potential charge energy indicator by it. It does not depend on the value of q that is placed in the region. Since the potential energy indicator depends on which coordinate system is chosen, the potential is determined accurate to a constant. It is equal to the work field that displaces a unit positive charge to infinity. Expressed through φ = W / q =const.
You may be interested in Features of calculating a voltage divider
Potential of a point in the field of a point charge
Note! In tasks, you can convert a constant. If W is unknown, then we can divide q by φ, and if q, then W by φ.
Potential charge energy in an electrostatic field
Potential energy of a charge in an electrostatic field
Since the work of an electric field does not depend on the chosen motion of the charged particle, but on its initial and final position, there is the term potential energy. This is a scalar quantity in a space coordinate that shows how the force works when a particle moves along an arbitrary interval from one point to another. It is equal to the difference in the values of particle movement in this interval. It is expressed in the following form: A = P1 - P2, where P1 can be x, y and z, and P2 can be x2, y2 and z2. In physics problems, you need to draw a graph, substitute known values into a constant, and solve equations.
Potential energy of charge q1 in the field of a point charge
When charged particles move across a field from one point to another, they perform some work over a certain time period. The potential energy at these points does not depend on which path the charged particles take. The energy of the first charge is proportional to its modulus. This is all expressed in the formula presented in the picture below. Problems can be solved by using the presented constant and inserting known values.
Potential energy of charge q1 in the field of a point charge
Gauss's theorem
The fundamental law in electrodynamics, included in Maxwell's equations. This is a consequence of the Coulomb inference and the principle of superposition. Along it, the field voltage vector moves through an arbitrary value of a closed surface surrounded by charges. It is proportional to the sum of charged particles that are inside this closed space. The specified vector is divided by e0. All this is expressed by the formula below.
Gauss's theorem
Electric field strength near the surface of the conductor
The intensity of the total space of charged particles is directly proportional to the surface indicator of their density. If the problem requires finding the tension, and the surface charged density is sigma, then you need to draw a cylinder and designate that the flux through its side surface is 0. In this case, the tension lines will be parallel to the side surface. It turns out that φ = 2φ, main = 2еs, and 2es = q / 2ε0.
Electric field strength near the surface of the conductor
Capacitance of parallel plate capacitor
Capacitance is a conductive characteristic through which an electric charge can accumulate energy. A flat capacitor is a series of oppositely charged plates separated by a thin dielectric layer. The capacitance of a flat capacitor is considered to be its characteristic, its ability to accumulate electrical energy.
Note! This is a physical quantity that is equal to the charge divided by the potential difference of its plate. The charge in this case is one charged plate.
If the problem requires finding out the capacitance of a capacitor made of two plates with an area of 10(-2) square meters and there is a 2*10(-3) meter sheet in them, ε0 is the electric constant with 8.85×10-12 farads per meter and ε =6 is the dielectric constant of mica. In this case, you need to insert the values into the formula C= ε* ε* S/d.
Capacitance of parallel plate capacitor
Energy of a parallel plate capacitor
Since any particle of a capacitor has the ability to store energy, which is stored on the capacitor plate, calculating this very E is simple, since in order for the element to charge, it needs to do work. The work is done by the field. As a result, the following formula was derived: Ep = A = qEd, where A is the work, d is the distance.
Energy