The interactions of electric charges were studied even before Charles Coulomb. In particular, the English physicist Cavendish in his research came to the conclusion that stationary charges, when interacting, obey a certain law. However, he did not make his findings public. Coulomb's law was rediscovered by a French physicist, after whom this fundamental law was named.
Figure 1. Coulomb's Law
History of discovery
Many physicists have carried out experiments with charged particles:
- G. V. Richman;
- professor of physics F. Epinus;
- D. Bernoulli;
- Priestley;
- John Robison and many others.
All these scientists came very close to discovering the law, but none of them managed to mathematically substantiate their guesses. Undoubtedly, they observed the interaction of charged balls, but establishing a pattern in this process was not easy.
Coulomb carried out careful measurements of the interaction forces. For this purpose, he even designed a unique device - a torsion balance (see Fig. 2).
Rice. 2. Torsion scales
The scales invented by Coulomb had extremely high sensitivity. The device responded to forces of the order of 10-9 N. The yoke of the scales, under the influence of this tiny force, rotated by 1º. The experimenter could measure the angle of rotation, and therefore the applied force, using an accurate scale.
Thanks to the scientist’s brilliant guess, the idea was that when charged and uncharged balls came into contact, the electric charge was divided equally between them. The torsion scales immediately responded to this, the beam of which was rotated to a certain angle. By grounding the stationary ball, Coulomb could neutralize the resulting charge on it.
Thus, the scientist was able to reduce the initial charge of the moving ball a multiple of times. Measuring the angle of deflection after each division of the charge, Coulomb saw a pattern in the action of the repulsive force, which helped him formulate his famous law.
Coulomb's law. Point charge.
The forces of electrostatic interaction depend on the shape and size of the electrified bodies, as well as on the nature of the charge distribution on these bodies. In some cases, we can neglect the shape and size of charged bodies and assume that each charge is concentrated at one point.
A point charge is an electric charge when the size of the body on which this charge is concentrated is much smaller than the distance between the charged bodies. Approximately point charges can be obtained experimentally by charging, for example, fairly small balls.
The interaction of two point charges at rest determines the basic law of electrostatics - Coulomb's law . This law was experimentally established in 1785 by the French physicist Charles Augustin Coulomb (1736 – 1806). The formulation of Coulomb's law is as follows:
The force of interaction between two point stationary charged bodies in a vacuum is directly proportional to the product of the charge modules and inversely proportional to the square of the distance between them.
This interaction force is called Coulomb force , and the formula for Coulomb's law will be as follows:
F = k (|q1| |q2|) / r2
where |q1|, |q2| – charge modules, r – distances between charges, k – proportionality coefficient.
The coefficient k in SI is usually written in the form:
k = 1 / (4πε0ε)
where ε0 = 8.85 * 10-12 C/N*m2 is the electrical constant, ε is the dielectric constant of the medium.
For vacuum ε = 1, k = 9 * 109 N*m/Cl2.
The force of interaction between stationary point charges in a vacuum:
F = [1 /(4πε0)] [(|q1| |q2|) / r2]
If two point charges are placed in a dielectric and the distance from these charges to the boundaries of the dielectric is significantly greater than the distance between the charges, then the force of interaction between them is equal to:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
The dielectric constant of a medium is always greater than unity (π > 1), therefore the force with which charges interact in a dielectric is less than the force of their interaction at the same distance in a vacuum.
The forces of interaction between two stationary point charged bodies are directed along the straight line connecting these bodies (Fig. 1.8).
Rice. 1.8. Forces of interaction between two stationary point charged bodies.
Coulomb forces, like gravitational forces, obey Newton's third law:
F1,2 = -F2,1
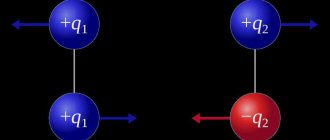
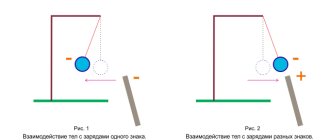
The Coulomb force is a central force. As experience shows, like charged bodies repel, oppositely charged bodies attract.
The vector of force F2,1 acting from the side of the second charge on the first is directed towards the second charge if the charges are of different signs, and in the opposite direction if the charges are of the same sign (Fig. 1.9).
Rice. 1.9. Interaction of unlike and like electric charges.
Electrostatic repulsive forces are considered to be positive, while attractive forces are considered negative. The signs of the interaction forces correspond to Coulomb's law: the product of like charges is a positive number, and the repulsive force has a positive sign. The product of opposite charges is a negative number, which corresponds to the sign of the force of attraction.
In Coulomb's experiments, the interaction forces of charged balls were measured, for which torsion balances (Fig. 1.10). A light glass rod with
, at one end of which a metal ball
a
, and at the other a counterweight
d
.
The upper end of the thread is fixed to the rotating head of the device e
, the angle of rotation of which can be accurately measured.
Inside the device there is a metal ball of the same size b
, fixedly mounted on the lid of the scale.
All parts of the device are placed in a glass cylinder, on the surface of which there is a scale that allows you to determine the distance between balls a
and
b
at their different positions.
Rice. 1.10. Coulomb experiment (torsion balance).
When the balls are charged with the same charges, they repel each other. In this case, the elastic thread is twisted at a certain angle to hold the balls at a fixed distance. The angle of twist of the thread determines the force of interaction between the balls depending on the distance between them. The dependence of the interaction force on the magnitude of the charges can be established as follows: give each of the balls a certain charge, place them at a certain distance and measure the angle of twist of the thread. Then you need to touch one of the balls with a charged ball of the same size, changing its charge, since when bodies of equal size come into contact, the charge is distributed equally between them. To maintain the same distance between the balls, it is necessary to change the angle of twist of the thread, and therefore, determine a new value of the interaction force with a new charge.
Formulation
Coulomb studied the interaction between balls of negligible size compared to the distances between them. In physics, such charged bodies are called point bodies. In other words, such charged bodies fall under the definition of point charges if their dimensions, under the conditions of a particular experiment, can be neglected.
For point charges, the following statement is true: The interaction forces between them are directed along a line passing through the centers of the charged bodies. The absolute magnitude of each force is directly proportional to the product of the charges and inversely proportional to the square of the distance between them (see Fig. 3). This dependence can be expressed by the formula: |F1|=|F2|=(ke*q1*q2) / r2
Rice. 3. Interaction of point charges
It remains to add that the force vectors are directed towards each other for unlike charges, and in the opposite direction in the case of like charges. That is, there is electrical attraction between like charges, and repulsion between like charges.
Thus, Coulomb's law describes the interaction between two electric charges, which underlies all electromagnetic interactions.
In order for the above law to apply, the following conditions must be met:
- compliance with point charges;
- immobility of charged bodies;
- the law expresses the relationships between charges in a vacuum.
Limits of application
The pattern described above, under certain conditions, is applicable to describe the processes of quantum mechanics. True, Coulomb's law is formulated without the concept of force. Instead of force, the concept of potential energy of the Coulomb interaction is used. The pattern was obtained by generalizing experimental data.
It should be noted that at ultra-short distances (during interactions of elementary particles) of the order of 10 - 18 m, electroweak effects appear. In these cases, Coulomb's law, strictly speaking, is no longer observed. The formula can be applied subject to amendments.
Violation of Coulomb's law is also observed in strong electromagnetic fields (about 1018 V/m), for example, near magnetars (a type of electron star). In such an environment, the Coulomb potential decreases not in inverse proportion, but exponentially.
Coulomb forces are subject to Newton's third law: F1 = – F2 . They are used to describe the laws of gravity. In this case, the formula takes the form: F = ( m1* m2 ) / r2 , where m1 and m2 are the masses of interacting bodies, and r is the distance between them.
Coulomb's law became the first open quantitative fundamental law substantiated mathematically. Its importance in the study of electromagnetic phenomena can hardly be overestimated. Since the discovery and promulgation of Coulomb's law, the era of the study of electromagnetism, which is of great importance in modern life, began.
Proportionality factor k and electrical constant
In the formula of Coulomb's law there are parameters k - the proportionality coefficient or - the electrical constant. The electric constant is presented in many reference books, textbooks, and the Internet, and you don’t need to count it! The proportionality coefficient in a vacuum based can be found using the well-known formula:
Here is the electric constant,
- Pi,
is the proportionality coefficient in vacuum.
Additional Information! Without knowing the parameters presented above, it will not be possible to find the force of interaction between two point electric charges. Formulation and formula of Coulomb's law
To summarize the above, it is necessary to give the official formulation of the main law of electrostatics. It takes the form:
The force of interaction between two point charges at rest in a vacuum is directly proportional to the product of these charges and inversely proportional to the square of the distance between them. Moreover, the product of charges must be taken modulo!
In this formula, q1 and q2 are point charges of the bodies being considered; r2 is the distance on the plane between these bodies, taken in square; k - proportionality coefficient (for vacuum).
Factor k
The formula contains the proportionality coefficient k, which is used to harmonize proportionality in the international SI system. In this system, the unit of measurement of charge is usually called the coulomb (C) - a charge passing through a conductor in 1 second, where the current is 1 A.
The coefficient k in SI is expressed as follows: k = 1/4πε0 , where ε0 is the electrical constant: ε0 = 8.85 ∙10-12 C2/N∙m2. After performing simple calculations, we find: k = 9×109 H*m2 / Cl2 . In the GHS metric system k =1.
Based on experiments, it was established that Coulomb forces, as well as the principle of superposition of electric fields, are described in the laws of electrostatics by Maxwell’s equations.
If several charged bodies interact with each other, then in a closed system the resulting force of this interaction is equal to the vector sum of all charged bodies. In such a system, electrical charges do not disappear - they are transferred from body to body.
Coulomb's law
- home
- Directory
- Laws
- Coulomb's law
Coulomb's law quantitatively describes the interaction of charged bodies. It is a fundamental law, that is, it was established through experiment and does not follow from any other law of nature. It is formulated for stationary point charges in a vacuum. In reality, point charges do not exist, but charges whose sizes are significantly smaller than the distance between them can be considered such. The force of interaction in air is almost no different from the force of interaction in vacuum (it is weaker by less than one thousandth).
Electric charge is a physical quantity that characterizes the property of particles or bodies to enter into electromagnetic force interactions.
The law of interaction of stationary charges was first discovered by the French physicist C. Coulomb in 1785. In Coulomb's experiments, the interaction between balls whose dimensions were much smaller than the distance between them was measured. Such charged bodies are usually called point charges .
Based on numerous experiments, Coulomb established the following law:
The force of interaction between two stationary point electric charges in a vacuum is directly proportional to the product of their moduli and inversely proportional to the square of the distance between them. It is directed along the straight line connecting the charges, and is an attractive force if the charges are opposite, and a repulsive force if the charges are like.
If we denote the charge modules by | q
1|
and | q
2|, then Coulomb’s law can be written in the following form:
\[ F = k \cdot \dfrac{\left|q_1 \right| \cdot \left|q_2 \right|}{r^2} \]
The proportionality coefficient k in Coulomb's law depends on the choice of unit system.
\[ k=\frac{1}{4\pi \varepsilon _0} \]
The full formula of Coulomb's law:
\[ F = \dfrac{\left|q_1 \right|\left|q_2 \right|}{4 \pi \varepsilon_0 \varepsilon r^2} \]
Where :
\( F \) — Coulomb force
\( q_1 q_2 \) — Electric charge of the body
\( r \) — Distance between charges
\( \varepsilon_0 = 8.85*10^{-12} \) — Electric constant
\( \varepsilon \) — Dielectric constant of the medium
\( k = 9*10^9 \) — Proportionality coefficient in Coulomb’s law
Interaction forces obey Newton's third law: \( \vec{F}_{12}=\vec{F}_{21} \) . They are repulsive forces with the same signs of charges and attractive forces with different signs.
Electric charge is usually denoted by the letters q or Q.
The totality of all known experimental facts allows us to draw the following conclusions:
- There are two types of electric charges, conventionally called positive and negative.
- Charges can be transferred (for example, by direct contact) from one body to another. Unlike body mass, electric charge is not an integral characteristic of a given body. The same body under different conditions can have a different charge.
- Like charges repel, unlike charges attract. This also reveals the fundamental difference between electromagnetic forces and gravitational ones. Gravitational forces are always attractive forces.
The interaction of stationary electric charges is called electrostatic or Coulomb interaction. The branch of electrodynamics that studies the Coulomb interaction is called electrostatics.
Coulomb's law is valid for point charged bodies. In practice, Coulomb's law is well satisfied if the sizes of charged bodies are much smaller than the distance between them.
Note that for Coulomb’s law to be satisfied, 3 conditions are necessary:
- Pointedness of charges - that is, the distance between charged bodies is much larger than their sizes.
- Immobility of charges . Otherwise, additional effects come into force: the magnetic field of a moving charge and the corresponding additional Lorentz force acting on another moving charge.
- Interaction of charges in vacuum.
In the International SI system, the unit of charge is the coulomb (C).
A coulomb is a charge passing through the cross-section of a conductor in 1 s at a current of 1 A. The unit of current (Ampere) in SI is, along with units of length, time and mass, the basic unit of measurement.
Laws Formulas Physics Theory Electricity Law
More interesting things in telegram @calcsbox
Coulomb's law in dielectrics
It was mentioned above that the formula determining the dependence of force on the size of point charges and the distance between them is valid for vacuum. In a medium, the force of interaction decreases due to the phenomenon of polarization. In a homogeneous isotopic medium, the decrease in force is proportional to a certain value characteristic of this medium. This quantity is called the dielectric constant. Another name is dielectric constant. It is denoted by the symbol ε. In this case k = 1/4πεε0.
The dielectric constant of air is very close to 1. Therefore, Coulomb's law in air space manifests itself in the same way as in vacuum.
An interesting fact is that dielectrics can accumulate electrical charges, which form an electric field. Conductors do not have this property, since charges falling on the conductor are almost immediately neutralized. To maintain an electric field in a conductor, it is necessary to continuously supply charged particles to it, forming a closed circuit.
Pendant.
A coulomb is a unit of measurement of electrical charge (amount of electricity) as well as the flux of electrical induction (flux of electrical displacement) in the International System of Units (SI). It has a Russian designation - Kl and an international designation - C.
Pendant as a unit of measurement
Application of the pendant
Representation of a pendant in other units of measurement - formulas
Multiples and submultiples of coulomb units
Interesting examples
Other units of measurement
Application in practice
All modern electrical engineering is built on the principles of interaction of Coulomb forces. Thanks to Clone's discovery of this fundamental law, an entire science has developed that studies electromagnetic interactions. The concept of the term electric field is also based on knowledge of Coulomb forces. It has been proven that the electric field is inextricably linked with the charges of elementary particles.
Thunderclouds are nothing more than a collection of electrical charges. They attract induced earth charges towards themselves, resulting in lightning. This discovery made it possible to create effective lightning rods to protect buildings and electrical structures.
Many inventions have appeared based on electrostatics:
- capacitor;
- various dielectrics;
- antistatic materials to protect sensitive electronic parts;
- protective clothing for electronics industry workers and much more.
The operation of charged particle accelerators, in particular, the operation of the Large Hadron Collider (see Fig. 4), is based on Coulomb’s law.
Rice. 4. Large Hadron Collider
Acceleration of charged particles to near-light speeds occurs under the influence of an electromagnetic field created by coils located along the path. Elementary particles disintegrate from the collision, traces of which are recorded by electronic devices. Based on these photographs, applying Coulomb's law, scientists draw conclusions about the structure of the elementary building blocks of matter.
References:
- Sivukhin D.V. General course in physics. - M.: Fizmatlit; Publishing house MIPT, 2004.
- Landau L. D., Lifshits E. M. Theoretical physics: Textbook. manual: For universities.
- Landsberg G.S. Elementary physics textbook. Volume II. Electricity and magnetism.
Pendant as a unit of measurement:
A coulomb is a unit of measurement of electrical charge (amount of electricity) as well as flux of electrical induction (flux of electrical displacement) in the International System of Units (SI), named after the French physicist and engineer Charles Coulomb.
The pendant as a unit of measurement has a Russian designation - Kl and an international designation - S.
1 coulomb is defined as the amount of charge passing through a conductor at a current of 1 ampere in 1 second.
Cl = A · s.
1 C = 1 A s = 1/3600 ampere hour.
The charge of one pendant is very large. If two charge carriers (q1 = q2 = 1 C) were placed in a vacuum at a distance of 1 m, then they would interact with a force of 9⋅109 N, that is, with the force with which the Earth’s gravity attracts an object weighing about 1 million tons.
Electric charge (amount of electricity) is a physical scalar quantity. Electric charge carriers are electrically charged elementary particles (electron, positron, proton, etc.). The smallest particle by mass that is stable in a free state and has one negative elementary electric charge is the electron. The electric charge of an electron is indivisible and equal to -1.6021766208(98)⋅10−19 C. The charge of a proton is also equal to the charge of an electron, but with the opposite sign (+ sign) and is equal to +1.6021766208(98)⋅10−19 C.
Thus, the elementary electric charge (to within a sign equal to the charge of an electron or proton) is the above value +/- 1.602176 6208(98)⋅10−19 C. Accordingly, the electric charge of 6.24151⋅1018 electrons is equal to -1 C, and the electric charge of 6.24151⋅1018 protons is equal to +1 C. In this case, the mass of the electron is 9.10938356(11)⋅10−31 kg, and that of the proton is 1.672 621 923 69(51)⋅10−27 kg.
The smallest antiparticle stable in a free state with a positive elementary charge is the positron, which has the same electric charge as the electron, but with a + sign. The electric charge of a positron is +1.6021766208(98)⋅10−19 C. The positron mass is 9.10938356(11)⋅10−31.
The coulomb was introduced into the International System of Units by the decision of the XI General Conference on Weights and Measures in 1960, simultaneously with the adoption of the SI system as a whole. In accordance with the SI rules regarding derived units named after scientists, the name of the unit “coulomb” is written with a lowercase letter, and its designation with a capital letter (Cl). This spelling of the designation is also preserved in the designations of derived units formed using a pendant.
Coulomb's law for charges in vacuum
Let's consider two point charges that are in vacuum (Fig. 2).
Rice. 2. Two positive charges q and Q, located in a vacuum at a distance r, repel. The repulsive forces are directed along the straight line connecting the charges
In Figure 2, the force \(\large F_{Q}\) is the force with which a positive charge Q repels a second positive charge q. And the force \(\large F_{q} \) belongs to the charge q, with such a force it repels the charge Q.
Note: A point charge is a charged body whose size and shape can be neglected.
The forces of interaction between charges, according to Newton's third law, are equal in magnitude and opposite in direction. Therefore, for convenience, you can introduce the notation:
\[\large F_{q} = F_{Q} = F\]
For the force of interaction of charges in a vacuum, Charles Coulomb formulated the law as follows:
Two point charges in a vacuum interact with a force directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them.
The formula for this law in the language of mathematics will be written as follows:
\[\large \boxed { F = k \cdot \frac {|q| \cdot |Q| }{r^{2}} } \]
\(F \left( H \right) \) – the force with which two point charges attract or repel;
\(|q| \left( \text{Cl}\right) \) – the value of the first charge;
\(|Q| \left( \text{Cl}\right) \) – the value of the second charge;
\(r \left( \text{m}\right) \) – distance between two point charges;
\(k\) – constant value, coefficient in the SI system;
Force is a vector. The two main characteristics of a vector are its length and direction.
The formula allows you to find one of the characteristics of the vector F - the modulus (length) of the vector.
To determine the second characteristic of vector F - its direction, you need to use the rule: Mentally connect two stationary point charges with a straight line. The force with which they interact will be directed along this straight line.
The Coulomb force is a central force, since it is directed along a straight line connecting the centers of the bodies.
Note: Another example of a central force is gravity.
What is coefficient k from the point of view of physics
The constant value \(k\), included in the formula for the force of interaction of charges, has the following physical meaning:
\(k\) is the force with which two positive point charges of 1 C each repel when the distance between them is 1 meter.
The value of the constant k is nine billion!
\[\large \boxed { k = 9\cdot 10^{9} \left( H \cdot \frac{\text{m}^{2}}{\text{Kl}^{2}}\right) } \]
This means that the charges interact with great forces.
Rice. 3. Coefficient k in the charge interaction formula
The constant k can be calculated experimentally by placing two known charges (not necessarily 1 Coulomb each) at a convenient distance for measurements (not necessarily 1 meter) and measuring the force from the mutual action.
It is necessary to substitute the known values of the charges, the distance between them and the measured force into the following formula:
\[\large \boxed { k = \frac {F \cdot r^{2}}{|q| \cdot |Q|} } \]
The value of k is related to the electrical constant \(\varepsilon\) by the following formula:
\[\large \boxed { k = \frac{1}{4\pi \cdot \varepsilon_{0}} } \]
Therefore, the fraction from the right side of this formula can be found in various physics reference books, where it replaces the coefficient k.
Basic law of electrostatics
In 1785, Coulomb presented a report to the Paris Academy of Sciences in which he described the design and use of the electric scales he had designed. The operating principle of the mechanism is based on the torsional properties of metal wire. While working on the design of the device, the researcher drew attention to the dependence of the force acting on objects on the distance between them.
The definition of the law discovered by the French scientist states: “Two identical balls, charged with electricity of the same polarity, repel each other with a force, the magnitude of which is inversely proportional to the square of the distance between the central points of the balls.” The literal implementation of the rule depends on three circumstances. Conditions necessary to comply with the law:
- the size of the charges is several times smaller than the distance between them, that is, they must be pointlike;
- immobility;
- charges are placed in a vacuum.
Mathematical expression
Coulomb's law, the formula of which resembles the mathematical formulation of Newton's law of universal gravitation, is one of the fundamental ones. This means that the discovery is based on experimental research. In addition, the discovered patterns do not follow from another law of physics. The law of interaction of two electric charges in a vacuum is described by the formula F = k ∙ (q₁ ∙ q₂) ∕ r2, where:
- F is the Coulomb force;
- k is the proportionality coefficient in Coulomb’s law;
- q₁, q₂—electric charge of each body, measured in coulombs;
- r is the distance between the bodies.
The proportionality coefficient k = 9 ∙ 10⁹ is calculated from the equation k = 1 ∕ 4πε₀, where ε₀ is the electrical constant equal to 8.85 ∙ 10⁻¹².
Taking into account the dielectric constant of the medium ε in which the objects are placed, the Coulomb formula takes the full form: F = (q₁ ∙ q₂) ∕ 4πε₀ε r2.
The coefficient ε shows how many times the Coulomb force weakens. For example, for kerosene ε = 2.1, and for sulfuric acid ε = 101. This means that bodies immersed in kerosene interact with a force 2.1 times less than in vacuum, and in sulfuric acid F will decrease by 101 once.
Coulomb's law in vector form is as follows: F ̅₁₂ = ∙ (r ̄₁₂ ∕ r ₁₂), where:
- F ̅₁₂ is the vector of force acting on the second charge from the first;
- r ̄₁₂ is the radius of the vector directed from the first charge to the second and in absolute value equal to the distance between the charged particles.
An electric charge creates a field in the space around itself, which is characterized by tension. If a charged particle is placed in it, then potential energy appears that can do work to move this particle. The potential, which characterizes the energy state of each point of the field, determines the amount of work that is done when a charge moves in an electrostatic field.
Historical meaning
The discovery made by Charles Coulomb gave impetus to further research in the field of electrical energy. Advances in science have accelerated the use of electrical engineering in human life. Scientists who continued work on the study of electricity:
- Hans Christian Oersted studied the effect of electric current on a compass needle;
- A.-M. Ampere studied the movement of electricity;
- M. Faraday discovered the phenomenon of electrolysis.
Coulomb laid the foundations of electrostatics. The principles of magnetostatics are based on the scientist’s work. The experiments carried out by Charles Augustin are of fundamental and applied importance. The Frenchman's experiments created a method for calculating a unit of charge using quantities that are used in mechanics - distance and force.
Coulomb was the first to formulate the interaction of charged particles in mathematical language.