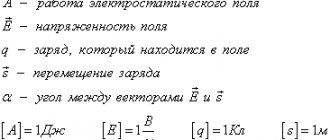Потенциал электрического поля — скалярная величина тела, характеризующая интенсивность. Электромощность выражается через определённый параметр. Важным свойством электрополя, которое не содержит вихрей и формируется недвижимыми источниками, считается его потенциальность. Научные работники длительное время думали над особенностями электрических и магнитных полей, пока их сущность в полной мере не стала ясной.
Вещественное значение электрического поля
Учёные длительное время изучали секрет электроэнергии. Главная награда в ее исследовании дана Эрстеду. Его основное открытие — впервые экспериментально установлена связь между электрическими и магнитными явлениями в 1819—1820 гг.
Стало ясно, что колебания предполагают суперпозицию изменяющихся во времени электрических и магнитных полей. Вектор магнитной интенсивности перпендикулярен электрическому вектору, связанному через длинную среду (некоторая физическая величина). Электростатическое воздействие — это действие через поле.
Особенности воздействия:
- Каждый электрический заряд создаёт вокруг себя электростатическое поле.
- Электрополем называется пространство, в котором действуют силы напряжения.
- Величины, характеризующие поле в этой точке, — это интенсивность и потенциал.
Напряжённостью электростатического явления в этой точке называется отношение электросилы, действующей на помещённый в этой точке пробный заряд (положительный) к значению этого заряда:
- E =F /q (над E и F вектор).
- Единица напряжённости электростатического поля — 1 N/C.
Напряжённость электрополя в этой точке всегда имеет отдачу в соответствии с направлением силы, действующей на положительный пробный заряд.
Значение напряжённости электростатического поля на расстоянии R от источника Q может обозначаться простой формулой: E=k |Q|/R2.
Для графического представления поля используются линии — кривые, для которых вектор напряжённости в каждой точке имеет касательную часть. Поле со сферической симметрией называется центральным. Если линии расположены параллельно друг другу, а интенсивность имеет в каждой точке одинаковое значение, то поле называется однородным.
Разность потенциалов в физике в данный момент — это отношение энергии точечного положительного пробного груза, помещённого в этой точке к значению этого заряда: V=Ep/q.
Единицей измерения потенциала точки электрического поля является 1 В (вольт).
Потенциал электрического поля, формула на расстоянии R от источника Q можно рассчитать: V=k Q/r.
Измерение напряжения осциллографом
Иллюстрацией к вышесказанному будет серия опытов по измерению напряжений с использованием генератора сигналов, источника постоянного напряжения, осциллографа и многофункционального цифрового прибора (мультиметра).
Эксперимент №1
Общая схема эксперимента №1 представлена ниже:
Генератор сигналов нагружен на сопротивление нагрузки R1 в 1 кОм, параллельно сопротивлению подключены измерительные концы осциллографа и мультиметра. При проведении опытов учтём то обстоятельство, что рабочая частота осциллографа значительно выше рабочей частоты мультиметра.
Опыт 1:
Подадим на сопротивление нагрузки сигнал синусоидальной формы с генератора частотой 60 герц и амплитудой 4 вольт. На экране осциллографа будем наблюдать изображение, показанное ниже. Отметим, что цена деления масштабной сетки экрана осциллографа по вертикальной оси 2 В. Мультиметр и осциллограф при этом покажут среднеквадратичное значение напряжение 1,36 В.
Опыт 2:
Увеличим сигнал от генератора вдвое, размах изображения на осциллографе возрастёт ровно вдвое и мультиметр покажет удвоенное значение напряжения:
Опыт 3:
Увеличим частоту генератора в 100 раз (6 кГц), при этом частота сигнала на осциллографе изменится, но размах и среднеквадратичное значение останутся прежними, а показания мультиметра станут неправильными — сказывается допустимый рабочий частотный диапазон мультиметра 0—400 Гц:
Опыт 4:
Вернёмся к исходной частоте 60 Гц и напряжению генератора сигналов 4 В, но изменим форму его сигнала с синусоидальной на треугольную. Размах изображения на осциллографе остался прежним, а показания мультиметра уменьшились по сравнению со значением напряжения, которое он показывал в опыте №1, так как изменилось действующее напряжение сигнала:
Эксперимент №2
Схема эксперимента №2, аналогична схеме эксперимента 1.
Ручкой изменения напряжения смещения на генераторе сигналов добавим смещение 1 В. На генераторе сигналов установим синусоидальное напряжение с размахом 4 В с частотой 60 Гц — как и в эксперименте №1. Сигнал на осциллографе поднимется на половину большого деления, а мультиметр покажет среднеквадратичное значение 1,33 В. Осциллограф покажет изображение, подобное изображению из опыта 1 эксперимента №1, но поднятое половину большого деления. Мультиметр покажет почти такое же напряжение, как было в опыте 1 эксперимента №1, так как у него закрытый вход, а осциллограф с открытым входом покажет увеличенное действующее значение суммы постоянного и переменного напряжений, которое больше действующего значения напряжения без постоянной составляющей:
Заряд вокруг объекта
Конечно, можно говорить о поле, если есть какой-либо его источник. Каждое электрическое тело создаёт вокруг себя градиент потенциала электрического поля. По сравнению с гравитационными полями, есть важное отличие:
- Гравитационные силы являются силами притяжения и могут измеряться.
- Силы электричества могут быть как силами притяжения, так и отталкивания.
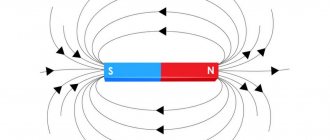
Известно, что линии поля относятся к векторам силы, действующим на тело в этой точке. Учёные сошлись во мнении, что стрелки линии поля будут выставлять обратный вектор силы, действующей на отрицательный заряд. Следовательно, силовые линии «выходят» из зарядов положительных и «бегут» к отрицательным энергетическим зарядам.
Напряжённость электрополя
В электрическом поле, так же как и в гравитационном, возникает понятие напряжённости. Это говорит о том, какая сила будет действовать, а известно, что эта сила зависит от источника и от расстояния. Именно интенсивность — характеристика этого поля, которое можно зарядить. По определению, напряжённость электрополя — это отношение силы, действующей на его значение.
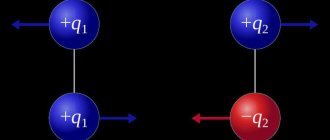
Если поле не вызвано одним источником, а, например, двумя положительными зарядами, то для вычисления интенсивности в этой точке пространства есть смысл применить принцип суперпозиции.
Например, есть данные центрального поля, создаваемые зарядом Q. Следует разместить на расстоянии R1 пробный заряд q. Делается работа по перемещению этого испытательного заряда на расстояние R2 от источника поля.
Для того чтобы система заряда двигалась с одинаковой скоростью, нужно постоянно действовать на него с усилием, уравновешивающем величину Куломба. Но вместе с изменением расстояния от источника эта сила меняется обратно пропорционально квадрату расстояния. Использовать нужно среднюю величину, действующую на пробный заряд.
Чтобы определить, является ли работа положительной или отрицательной, нужно подумать, каков угол между вектором приложенного усилия и вектором перемещения. Если пробный заряд притягивается источником поля, и работа, которую выполняют, перемещает этот заряд ближе к источнику, тогда нужно сбалансировать притяжение.
Одним словом, прилагают усилие, которое создаёт с вектором смещение на угол 180°. Если cos (α)= -1, то работа отрицательная. Но если источник имеет взаимодействие с грузом так, чтобы уравновесить силу, параллельную цепи смещения, так что условие α=0°, т. е. cos (α) = 1 — работа положительная.
Потенциал электростатического поля и разность потенциалов
В механике взаимное действие тел друг на друга характеризуют силой или потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризую двумя величинами, Напряженность поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал.
Потенциал поля. Работа любого электростатического поля при перемещении в нем заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля. На замкнутой траектории работа электростатического поля всегда равна нулю. Поля, обладающие таким свойством, называют потенциальными. Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.
Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А= — (WP1 — WP2) справедлива для любого электростатического поля. И только в случае однородного поля потенциальная энергия выражается формулой Wp=qEd.
Потенциал
Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля, так и для любого другого. Следовательно, отношение потенциальной энергии к заряду не зависит от помещенного в поле заряда.
Это позволяет ввести новую количественную характеристику поля — потенциал, не зависящую от заряда, помещенного в поле.
Потенциалом электростатического поля называют отношение потенциальной энергии заряда в поле к этому заряду.
Согласно данному определению потенциал равен:
(1)
Напряженность поля является вектором и представляет собой силовую характеристику поля; она определяет силу, действующую на заряд q в данной точке поля. Потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
Если в качестве нулевого уровня потенциальной энергии, а значит, и потенциала принять отрицательно заряженную пластину, то согласно формулам Wp=qEd и (1) потенциал однородного поля равен:
(1)
Разность потенциалов
Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Практическое значение имеет не сам потенциал в точке, а изменение потенциала, которое не зависит от выбора нулевого уровня отсчета потенциала.
Так как потенциальная энергия Wp = qφ, то работа равна:
(2)
Здесь
(3)
разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Разность потенциалов называют также напряжением.
Согласно формулам (2) и (3) разность потенциалов оказывается равной:
(4)
Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении заряда из начальной точки в конечную к этому заряду.
Зная напряжение в осветительной сети, мы тем самым знаем работу, которую электрическое поле может совершить при перемещении единичного заряда от одного контакта розетки к другому по любой электрической цепи. С понятием разности потенциалов мы будем иметь дело на протяжении всего курса физики.
Единица разности потенциалов
Единицу разности потенциалов устанавливают с помощью формулы (4). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах. Поэтому разность потенциалов между двумя точками равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В); 1 В = 1 Дж/1 Кл.
Энергетическую характеристику электростатического поля называют потенциалом. Потенциал равен отношению потенциальной энергии заряда в поле к заряду. Разность потенциалов между двумя точками равна работе по перемещению единичного заряда.
Потенциальная энергия
Вычисляя потенциальную энергию испытательного заряда в этой точке поля, используют свойство, при котором разница потенциальной энергии в двух точках равна работе, выполняемой при перемещении этого значения из одной точки в другую (то же самое делали, включая энергию в гравитационном поле).
Для того чтобы вычислить потенциальную энергию в этой точке, нужно переместить пробный заряд в место, где потенциал равен нулю. Такое место находится в точке, бесконечно отдалённой от источника. Положительный или отрицательный знак потенциала выбирают в зависимости от того, отталкивают груз с источником или притягивают. Если заряд источника является отрицательным, то нахождение электростатического потенциала является таким же. Когда источник является положительным, потенциал — тоже.
Эквипотенциальные поверхности
Если предположить, что источником электрополя является точечно заряженная частица (т. е. поле центральное), из этого следует, что все точки пространства, которые находятся от него одинаково далеко, имеют равный потенциал. В пространстве совокупность таких точек образует поверхность шара, а заряд-источник находится в центре сферы.
Однако, если электрополе не имеет централизованного характера, всё равно можно назначить такие поверхности, что пробный заряд, размещённый в любой точке этой поверхности, будет иметь тот же потенциал. Например, в случае однородного поля такой поверхностью является любая плоскость, перпендикулярная линии поля.
Тема 3. Потенциалы полей различных заряженных тел.
1. Электрон с начальной энергией W
движется издалека в вакууме по направлению к центру равномерно заряженного шара радиуса
R.
Полагая заряд шара отрицательным и равным
q,
найдите минимальное расстояние г, на которое приблизится электрон к поверхности шара.
2. Найдите, чему равна работа при перенесении точечного заряда 20 нКл из бесконечности в точку, находящуюся на расстоянии 1 см от поверхности шара радиуса 1 см, заряженного с поверхностной плотностью заряда 1 нКл/см2.
3. Найдите работу (на единицу длины), которую нужно совершить, чтобы сблизить две одноименно заряженные длинные параллельные нити от расстояния 20 см до 10 см между ними. Линейная плотность зарядов каждой нити 3 мкКл/м. In 0,5 = — 0,69.
4. Тонкая прямая длинная нить равномерно заряжена с линейной плотностью заряда 2 мкКл/м. Найдите потенциал поля нити как функцию расстояния r
от нити. Вычислите потенциал на расстоянии 10 м, приняв
φ
=
0
на расстоянии 1 м.
5. В противоположных вершинах квадрата со стороной а
размещены два точечных заряда (+q) и (-
2q),
Найдите потенциал поля в каждой из незанятых вершин квадрата.
6. Тонкий стержень согнут в кольцо радиуса R,
равномерно заряженное с линейной плотностью
т.
Найдите потенциал поля в точке, расположенной на оси кольца на расстоянии
х
от его центра.
7. Заряд q
равномерно распределен по полукольцу радиуса R. Найдите потенциал в центре полукольца.
8. Кольцо радиуса R
из тонкой проволоки имеет заряд
q.
Найдите потенциал электрического поля в центре кольца, считая, что
φ=
0.
10 Электрическое поле создано двумя бесконечными параллельными плоскостями, заряженными с поверхностной плотностью 1 нКл/м2 и 5 нКл/м2. Найдите разность потенциалов между плоскостями, если расстояние между ними равно 5 мм.
11 Сфера радиуса R
равномерно заряжена с поверхностной плотностью заряда а. Найдите потенциал электрического поля на поверхности сферы, внутри и вне ее. Постройте график
φ(r).
12. Найдите потенциал в центре металлической сферы радиуса R,
заряженной однородно с поверхностной плотностью заряда σ.
13. Получите выражение для потенциала φ
поля плоского конденсатора в зависимости от координаты
х,
направленной перпендикулярно пластинам конденсатора. Нарисуйте графики зависимости
φ (х),
приняв
φ=
0:1) на первой пластине, 2) на второй пластине и 3) в плоскости, лежащей посередине между пластинами.
14 Тонкий стержень согнут в полукольцо и заряжен с линейной плотностью заряда 133 нКл/м. Найдите работу, которую надо совершить, чтобы перенести заряд 6,7 нКл из центра кривизны полукольца в бесконечность.
15.Кольцо радиуса R
заряжено с линейной плотностью заряда τ. Найдите работу сил поля по перемещению заряда
q
из центра кольца в точку, находящуюся на оси кольца на расстоянии 3
R
от его центра.
16.Вдоль силовой линии электрического поля отрицательно заряженной протяженной плоскости движется электрон. Найдите минимальное расстояние, на которое он может приблизиться к плоскости, если на расстоянии 5 см от плоскости кинетическая энергия электрона 8 кДж, а поверхностная плотность заряда плоскости 35,4 Кл/м² .
17.Две одинаковые сферы радиуса R
заряжены зарядами
+q
и
-q.
Найдите напряженность и потенциал поля в точке, лежащей посередине прямой, соединяющей центры сфер, если расстояние между центрами равно 10R.
НЗ.Тонкий диск радиуса R
равномерно заряжен с поверхностной плотностью заряда
σ.
Найдите потенциал поля в центре диска.
19.Найдите потенциалы в т. А
и С, считая, что потенциал в т.
В
равен 0.
Все точки лежат на одной силовой линии однородного электрического поля напряженностью 100 В/м.
а =1
см.Нарисуйте график зависимости
φ(х).
20.Три пластины расположены в вакууме параллельно друг другу. Расстояние от средней пластины до крайних d
и
2d.
На первой пластине равномерно распределен заряд с поверхностной плотностью +
σ
, на второй — (- 2
σ
), на третьей — (- 3
σ
). Найдите разность потенциалов между пластинами 1и 2,1 и 3,2 и 3.
21.Электрическое поле создано длинным цилиндром радиуса 1 см, равномерно заряженным с
линейной плотностью заряда 20 мКл/м. Найдите разность потенциалов двух точек этого поля, находящихся на расстояниях 0,5 см и 2 см от оси цилиндра в средней его части.