Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными
, а само поле называется
потенциальным
.
Определение электростатического потенциала
Тело, пребывающее в потенциальном поле сил (а электростатическое поле считается потенциальным), имеет потенциальную энергию, посредством которой силами поля будет совершаться работа. Работа консервативных сил будет выполняться за счет убыли потенциальной энергии
Электростатический потенциал является специальным термином в случае возможной замены общего термина в электродинамике (скалярный потенциал). Исторически в физике первым наблюдается появление термина «электростатический потенциал», а уже скалярный потенциал электродинамики стал его обобщением.
В связи с тем, что потенциал (равно как и потенциальная энергия) может определяться с точностью до произвольной постоянной (и все величины, которые возможно измерить: напряженности поля, силы, остаются неизменными в независимости от выбора способа постоянной величины) непосредственным физическим смыслом (если не имеются в виду квантовые эффекты) обладает не сам потенциал, а разность потенциалов.
При этом принято считать, что прочие заряды при подобной операции «заморожены» (неподвижны в момент такого перемещения (подразумевается воображаемое, а не реальное перемещение). При этом, в редких случаях, с целью снятия неоднозначности, используют определенные «естественные» условия.
Рисунок 2. Потенциал электростатического поля. Автор24 — интернет-биржа студенческих работ
Так, например, часто потенциал определяется таким образом, чтобы его значение оказывалось равнозначно нулевому на бесконечности для какого-либо точечного заряда. В такой ситуации для любой конечной системы зарядов будет выполнимо на бесконечности аналогичное условие, а над произволом выбора константы при этом можно будет не задумываться.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом
данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Работа в электрическом поле. Потенциал
При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна (рис. 1.4.1):
| Рисунок 1.4.1. Работа электрических сил при малом перемещении заряда q |
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение . Работа ΔA кулоновских сил на этом перемещении равна
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить
| Рисунок 1.4.2. Работа кулоновских сил при перемещении заряда q зависит только от расстояний r1 и r2 начальной и конечной точек траектории |
Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов , то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ кулоновских полей точечных зарядов: Так как каждый член суммы не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.
Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):
| Wp1 = A10. |
(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
| A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2. |
Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля.
Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2). |
В Международной системе единиц (СИ) единицей потенциала является Вольт (В).
| 1 В = 1 Дж / 1 Кл |
Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.
Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
| Рисунок 1.4.3. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда |
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать:
| ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ, |
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:
φ = φ1 + φ2 + φ3 + …
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
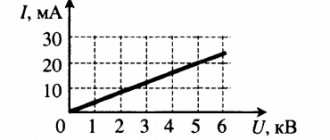
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Электростатическое поле
Электростатическое поле представляет образованное неподвижными в пространстве и неизменными во времени электрозарядами поле (при условии отсутствия электрических токов). Электрическое поле, таким образом, считается особым видом материи, связанным с электрическими зарядами и передающим воздействия зарядов друг на друга.
Так, при присутствии в пространстве системы заряженных тел, то в каждой его точке будет фиксироваться существование силового электрического поля, определяемого через силу, воздействующую на пробный точечный заряд, помещенный в данное поле. Пробный заряд должен при этом быть ничтожно малым, чтобы не оказать влияние на характеристику электростатического поля.
Помощь со студенческой работой на тему Потенциал в электростатике
Курсовая работа 460 ₽ Реферат 250 ₽ Контрольная работа 230 ₽
Получи выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Рисунок 1. Электростатическое поле. Автор24 — интернет-биржа студенческих работ
Электрическое поле называют однородным в ситуации, если вектор его напряженности оказывается одинаковым во всех точках поля. В качестве главных характеристик электростатического поля выделяют следующие:
- напряженность;
- потенциал.
Силовые линии такого поля обладают такими свойствами:
- Они будут всегда замкнутыми, то есть начинающимися на положительных зарядах и заканчивающимися на отрицательных. Они не пересекаются между собой и не касаются друг друга.
- Плотность линий тем больше, чем большей будет напряжённость. Другими словами, напряжённость поля является прямо пропорциональной количеству силовых линий, пересекающих площадку единичной площади, чье расположение будет перпендикулярно линиям.
Требуется консультация по учебной работе? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос
Замечание 1
Электростатическое поле оказывает непосредственное воздействие на любое количество зарядов, при этом возникнет сложная система взаимодействий. Напряженность системы можно рассматривать с точки зрения суперпозиции, поэтому суммарное влияние числа зарядов является векторной суммой всех напряженностей поля.
В соответствии с этим, чем больше таких линий, тем интенсивнее оказывается силовое воздействие. В металлах (и иных проводящих материалах) напряженность поля будет отсутствовать (за счет встречно направленного действия поля свободных носителей заряда, пребывающих в структуре кристаллической решетки).
Фактически, силы оперативно уравниваются, фиксируется отсутствие тока, а линии напряженности не способны проникнуть в такой проводник. Помимо векторных величин, поле может описываться скалярными значениями (идеальный случай), взятыми в каждой точке. Такие значения в электростатике характеризуют потенциал поля.