Для чего она нужна и где используется
Подобные элементы находят множество применений, но наиболее часто они используются в качестве:
- Элементов индуктивности в слаботочных электрических цепях;
- Реакторов в силовой электронике, в качестве элементов компенсации реактивного характера нагрузки;
- Дросселей для сглаживания пульсаций выпрямленного или переменного тока;
- Электромагнитов в качестве источников магнитного поля в электромагнитных реле или органах управления различных устройств;
- Индукторов в установках индукционного нагрева;
- Накопителя энергии в источниках преобразования напряжения;
- Датчиков магнитных полей (магнитные головки в накопителях на жестких магнитных дисках);
- Линий задержки сигнала;
- Антенн для приема и передачи электромагнитных волн.
Индуктивная антенна
Определение индуктивности, активного сопротивления катушки.
Для колебательного контура рекомендуется выбрать катушку 220/127 от школьного трансформатора, магазин конденсаторов Р544, выставив емкость порядка 0,5 мкФ, и магазин сопротивлений Р33.
Определить индуктивность и активное сопротивление катушки методом амперметра и вольтметра. Для этого собрать схему, указанную на (Рис. 4). При подключении в качестве источника тока постоянного выхода ВС-24 сопротивление rL
равно
,
а при подключении переменного выхода – сопротивление Z
равно:
,
откуда можно рассчитать индуктивность
L
:
.
Расчет параметров колебательного контура и экспериментальное получение затухающих колебаний.
Задав емкость конденсатора порядка 0,1 мкФ и активное сопротивление R
равное нулю, рассчитать параметры получившегося колебательного контура: частоту
n
(или
w
), коэффициент затухания
b
, период затухающих колебаний
Т
, логарифмический декремент затухания
d
, добротность колебательного контура
Q
, критическое сопротивление
Rкр
.
Собрать схему (Рис. 5), выставив на магазине емкостей 0,1 мкФ, на магазине сопротивлений – 0 Ом. Для того, чтобы картина затухающих колебаний была постоянно видна на экране осциллографа, необходимо периодически добавлять энергию в колебательный контур подзаряжая конденсатор. В качестве периодического источника энергии используется выход пилообразного
напряжения на правой боковой панели осциллографа. Частоту развертки осциллографа надо подобрать так, чтобы на один период развертки приходилось несколько периодов затухающих колебаний.
Конденсатор Сдиф
и входное сопротивление осциллографа
Rвх
представляют из себя дифференцирующую цепь, превращающую пилообразный сигнал в импульсный (Рис. 6). При плавном нарастании напряжения конденсатор успевает заряжаться, напряжение на нем в каждый момент времени практически равно напряжению источника пилообразного сигнала, и ток в цепи отсутствует. При резком уменьшении напряжения в цепи наблюдается импульс тока разрядки конденсатора. Выходное напряжение является дифференциалом входного напряжения по времени. Подобрать
Сдиф
порядка 100 ¸ 1000 пФ.
По полученной картине определить параметры колебательного контура и сравнить их с рассчитанными ранее. Меняя индуктивность катушки, вводя в нее сердечник, и емкость конденсатора, пронаблюдать и объяснить изменение картины затухающих колебаний.
Пронаблюдать изменение картины при увеличении активного сопротивления R
. Выставить на магазине сопротивлений такое
R
, чтобы выполнялось условие:
,
и убедиться, что колебания в контуре отсутствуют.
Вопросы к зачету по работе.
– Объяснить физический механизм электромагнитных колебаний в колебательном контуре.
– Как преобразуется энергия при электромагнитных колебаниях и чему равна полная энергия?
– Как влияет наличие активного сопротивления колебательного контура на электромагнитные колебания? Что такое затухающие электромагнитные колебания?
– Какие параметры контура определяют характер электромагнитных колебаний в контуре?
– Объяснить, почему наличие критического сопротивления в цепи препятствует возникновению электромагнитных колебаний в контуре.
Лабораторная работа № 10
Явления в цепях переменного тока
Цель работы.
Изучить закономерности явлений, наблюдаемых в цепях переменного тока.
Знания, необходимые для допуска к работе.
– Индуктивность и емкость в цепях переменного тока;
– Закон Ома для переменного тока;
– Резонансные явления в цепях переменного тока.
Краткие сведения из теории.
Переменным током называется любой ток, величина которого периодически меняется со временем. Но чаще всего под переменным током подразумевается ток, меняющийся по закону синуса (или косинуса):
,
где I
– амплитуда тока, – циклическая частота, а – фаза колебаний, характеризующая состояние колебательной системы в данный момент времени
t
.
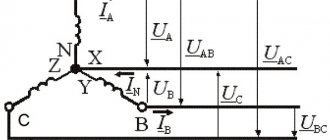
Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор, конденсатор и катушку индуктивности, подключенную к источнику переменного напряжения (Рис. 1). По этой цепи протекает ток, меняющийся по синусоидальному закону
.
Выходное напряжение источника тока при протекании постоянного тока по последовательному соединению проводников должно быть равно сумме падений напряжения на каждом проводнике:
,
но при переменном токе в цепи, содержащей емкость и индуктивность, есть некоторые отличия.
Падение напряжения на резисторе колеблется по такому же закону, как и ток
,
и их фазы колебаний совпадают.
Напряжение на обкладках конденсатора пропорционально заряду на них в каждый момент времени
,
а заряд можно определить как интеграл тока по времени
.
Тогда
.
Из этого выражения следуют два вывода: во-первых, колебания напряжения на конденсаторе отстают от колебаний тока на , а во-вторых, амплитудное значение напряжение связано с амплитудным значением тока соотношением:
,
где называется емкостным сопротивлением.
При протекании переменного тока через катушку в ней возникает ЭДС самоиндукции, препятствующая изменению тока
.
В этом случае для участка цепи, содержащего катушку (т.е. источник ЭДС, включенный навстречу току) падение напряжения равно
,
так как помимо ЭДС самоиндукции происходит падение напряжения на сопротивлении провода r
, из которого изготовлена катушка. Если предположить его малым, то и
.
Очевидно, что колебания напряжения на катушке опережают колебания тока на , а их амплитуды связаны соотношением
,
где – индуктивное сопротивление катушки.
Сопротивления R
,
r
называются активными (или омическими), а сопротивления
XL
и
XC
– реактивными.
Соотношения фаз колебаний напряжений на активных и реактивных сопротивлениях можно проиллюстрировать на векторной диаграмме (Рис. 2). За основное направление надо взять силу тока, так как он является общим для последовательно соединенных элементов схемы. Величину амплитуды выходного напряжения можно определить, используя закон сложения векторов:
.
Видно, что колебания напряжения и тока сдвинуты по фазе друг относительно друга на j
. Вынеся общий множитель – силу тока – из-под корня, получаем выражение:
,
где R
0 – все активное сопротивление электрической цепи. Это выражение является математической формулировкой закона Ома для переменной цепи. Общее сопротивление цепи
Z
и тангенс сдвига фаз между колебаниями тока и напряжения
tgj
определяется по формулам:
.
Как видно из этих формул, полное сопротивление цепи переменного тока зависит не только от величин активного сопротивления, индуктивности и емкости, но и от частоты переменного тока. При частоте близкой к нулю полное сопротивление цепи определяется емкостным сопротивлением и стремится к бесконечности, а сдвиг фаз . При высокой частоте переменного тока соответственно и .
Интересная ситуация наблюдается, когда частота переменного тока удовлетворяет условию:
.
В этом случае реактивная составляющая полного сопротивления равна нулю и, соответственно, полное сопротивление минимально и равно активному сопротивлению , а сдвиг фаз – нулю. Ток в этом случае приобретает максимальное значение . Такое состояние цепи переменного тока называется резонансом напряжений, а частота – резонансной частотой
wрез
.
Интересен также факт превышения напряжения на реактивных элементах схемы выходного напряжения источника тока. Если в момент резонанса индуктивное и емкостное сопротивления больше активного сопротивления цепи , то напряжения на них .
Практические задания
Свойства катушки
Устройства, которые состоят и витков провода, обладают рядом специфических свойств, среди которых можно отметить следующие:
- Ограничение скорости изменения тока, определяемое индуктивностью;
- Рост сопротивления при увеличении частоты протекающего тока;
- Накапливание энергии в собственном магнитном поле;
- Наличие ЭДС самоиндукции, пропорциональной скорости изменения тока;
- Сдвиг фазы тока в витках от напряжения (90° в цепях синусоидального тока).
Сдвиг фазы в катушке индуктивности
Свойства катушки индуктивности
Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току , поскольку при изменении тока в катушке возникает ЭДС самоиндукции , препятствующая этому изменению.
Катушка индуктивности обладает реактивным сопротивлением величина которого равна: , где- индуктивность катушки,-циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.
При протекании тока катушка запасает энергию, равную работе, которую необходимо совершить для установления текущего тока . Величина этой энергии равна
При изменении тока в катушке возникает ЭДС самоиндукции, значение которой
Конструкция катушки
Катушки индуктивности имеют множество разновидностей по конструктивным особенностям. В основе любой конструкции лежит от одного и более витков изолированного провода.
Различают следующие конструкции по типу обмоток:
- Соленоидальная – длина намотки многократно превышает диаметр;
- Тороидальная – когда соленоид свернут в форме тора.
- Многослойная – разновидность соленоида при наличии нескольких рядов обмоток;
- Секционированная – обмотки состоят из нескольких частей – секций;
- С намоткой «Универсал».
Вам это будет интересно Особенности расчета конденсатора
Две последних разновидности используются при необходимости снижения собственной паразитной емкости.
Секционированная катушка с обмоткой «универсал»
Важно! Все перечисленные разновидности могут быть выполнены с сердечником из ферромагнитного материала для увеличения индуктивности при сохранении габаритов.
Регулировка (изменение) индуктивности производится путем:
- Сдвига части витков в однослойных катушках;
- Изменением положения ферромагнитного сердечника;
- Переключением части витков;
- Изменение взаимного расположения обмоток, соединенных последовательно (вариометры).
Принцип действия
Принцип действия катушки индуктивности заключается в создании и взаимодействии магнитного потока витками обмотки.
Если взять в упрощенном случае единичный виток, то при прохождении через него электрического тока, создается магнитный поток, движущийся вдоль поверхности контура, пропорциональный величине тока и значению индуктивности:
Ф=L·I, где
Ф – магнитный поток;
L – индуктивность;
I – сила тока.
Важно! Катушки в подавляющем большинстве случаев представляют собой многовитковую конструкцию, поэтому образуют сложную поверхность и расчеты параметров производятся в упрощенном виде.
Магнитный поток соленоидальной катушки
Образование магнитного потока каждым из витков и взаимодействие его с остальными (магнитная индукция) приводит к возникновению ЭДС самоиндукции, которая заключается в том, что, при изменении величины протекающего тока в катушке, образуется ЭДС и, соответственно, ток, направленный, чтобы противодействовать изменениям.
В случае переменного тока это приводит к тому, что фаза тока отстает от фазы напряжения на 90°. Данное свойство используется в компенсаторах реактивного сопротивления (реакторах), дросселях, линиях задержки.
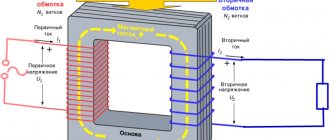
Важно! Величина ЭДС самоиндукции прямо пропорциональна скорости изменения тока. Это позволяет разрабатывать источники высоковольтного напряжения. Автомобильная катушка зажигания состоит из двух обмоток – низковольтной и высоковольтной. При размыкании питания в низковольтной обмотке в ней формируется импульс ЭДС самоиндукции, который в высоковольтной обмотке достигает десятков тысяч вольт.
Автомобильная катушка зажигания
Сопротивление катушки индуктивности включает две составляющих:
- Индуктивное сопротивление;
- Сопротивление потерь.
Вам это будет интересно Особенности коэффициента пульсации
Индуктивное сопротивление (реактивное сопротивление, импеданс) зависит от частоты протекающего тока:
XL = 2·π·f·L, где
π – 3.14;
f – частота;
L – индуктивность.
Сопротивление потерь включает в себя:
- Потери в проводах (активное сопротивление катушки);
- Потери на вихревые токи;
- Потери в сердечнике;
- Потери в диэлектрике.
Важно! Некоторые потери вносит также распределенная емкость, которую снижают путем использования особой конфигурации обмоток, разделения ее на секции.
Основную долю потерь вносит активное сопротивление.
Ёмкостное сопротивление
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.
Рисунок 2.
Мы можем использовать следующие соотношения:
Если $I(t)$ определена уравнением (1), то заряд выражен как:
где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $\frac{\pi }{2}.$ Амплитуда напряжения на емкости равна:
Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=\infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
Необходимо подобрать научные статьи для учебной работы? Укажи тему и получи ответ через 15 минут получить помощь
Активное сопротивление катушки
Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах, омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.
Обратите внимание! На высоких частотах проявляется скин-эффект, который заключается в том, что ток вытесняется в поверхностные слои провода. В результате этого снижается используемое сечение кабеля. Для снижения скин-эффекта вместо одного проводника используют жгут из нескольких более тонких – литцендрат, либо поверхность провода покрывают слоем серебра, поскольку оно обладает наименьшим удельным сопротивлением.
Скин-эффект
В мощных электромагнитных системах (ускорители частиц) для снижения активного сопротивления, используется свойство сверхпроводимости – полное исчезновение сопротивления при охлаждении некоторых материалов ниже критической температуры.
Провод литцендрат
Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами.
Активное сопротивление
Определение 1
Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:
\[I\left(t\right)=I_m{sin \left(\omega t\right)\ \left(1\right).\ }\]
Рисунок 1.
Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
\[U=IR=I_m{Rsin \left(\omega t\right)\ \left(2\right),\ }\]
где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
\[U_m=RI_m\left(3\right),\]
где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Готовые работы на аналогичную тему
- Курсовая работа Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока 450 руб.
- Реферат Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока 240 руб.
- Контрольная работа Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока 250 руб.
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость