Баланс мощностей
При решений электротехнических задач, часто нужно проверить правильность найденных значений. Для этого в науке ТОЭ, существует так называемый баланс мощностей.
Баланс мощностей – это выражение закона сохранения энергии, в электрической цепи. Определение баланса мощностей звучит так: сумма мощностей потребляемых приемниками, равна сумме мощностей отдаваемых источниками. То есть если источник ЭДС в цепи отдает 100 Вт, то приемники в этой цепи потребляют ровно такую же мощность.
Или
Проверим это соотношение на простом примере.
Для начала свернем схему и найдем эквивалентное сопротивление. R2 и R3 соединены параллельно.
Найдем по закону Ома ток источника и напряжение на R23, учитывая, что r1 и R23 соединены последовательно, следовательно, сила тока одинаковая.
Теперь проверим правильность с помощью баланса мощностей.
Небольшое различие в значениях связано с округлениями в ходе расчета.
С помощью баланса мощностей, можно проверить не только простую цепь, но и сложную. Давайте проверим сложную цепь из статьи метод контурных токов.
Как видите независимо от сложности цепи, баланс сошелся, и должен сойтись в любой цепи!
Источник
2.10. Мощность и ее составляющие в цепях переменного тока
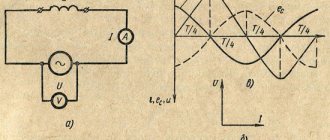
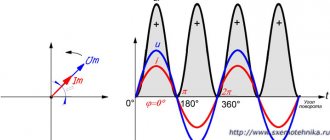
В цепях постоянного тока мощность нагрузок определялась по формуле: , а для источников: . В цепях переменного тока, если действовать по аналогии, мощность можно представить в виде: p = u i, то есть она изменяется во времени (см. разделы 2.5 и 2.6).
Если использовать комплексы, то мощность будет иметь вид: .
Но такая запись не всегда правильно отражает процессы. В этой формуле наблюдается зависимость результата от положения векторов на комплексной плоскости. Так, для нагрузки: ,
если угол напряжения больше нуля, а ток у такой нагрузки отстает от напряжения и если они расположены на комплексной плоскости (рис. 2.13), скалярное произведение двух комплексов равно произведению их модулей, а результирующий угол равен углу между векторами тока и напряжения, что не получается при перемножении комплексов:
Угол не равен углу между векторами тока и напряжения.
Для вычисления полной мощности в цепях переменного тока пользуются искусственным приёмом. В формуле полной мощности вместо комплекса тока подставляют комплексно-сопряженный ток:
или в алгебраической форме:
Если комплекс тока равен: , то комплексно-сопряженный ток находят так:
Баланс мощностей для цепей переменного тока составляется так:
Реактивная мощность в цепях переменного тока может быть как положительной так и отрицательной. У индуктивных нагрузок: , она больше нуля, а у емкостных нагрузок меньше нуля.
Источник
Баланс мощностей в цепях переменного тока
Комплексной мощностью называется произведение комплекса действующего значения напряжения на сопряжённый комплекс действующего значения тока .
Знак мнимой части сопряжённого комплекса изменён на обратный ( ) знак заданного комплексного числа (пример: , )).
Пусть на участке электрической цепи известно напряжение , ток . Сопряжённый ток равен: .
Тогда полная комплексная мощность данного участка равна:
где – сдвиг фаз между напряжением и током.
, [Вт] – активная мощность участка,
, [ВАр] – реактивная мощность участка.
Знак «+» перед соответствует индуктивному характеру сопротивления , знак «–» соответствует ёмкостному характеру .
При выполнении условия баланса мощностей активная и реактивная мощности источников питания должны равняться потребляемым активной и реактивной мощностям.
Мощности источника Э.Д.С. определяем по формуле:
где – сопряжённый комплекс тока в ветви с источником Э.Д.С.
Мощность источника тока:
где – напряжение на зажимах источника тока;
– сопряжённый ток источника тока.
Мощность источника Э.Д.С. входит в выражение баланса со знаком «+», если направление Э.Д.С. источника и тока в этой ветви совпадают; если направления Э.Д.С. источника и тока не совпадают, то мощность источника Э.Д.С. отрицательная.
Мощность источника тока входит в выражение баланса со знаком «+», если ток источника и напряжения на его зажимах направлены навстречу друг другу. При совпадении направлений тока источника и напряжения мощность источника отрицательная.
Активная и реактивная мощности потребителей равны соответственно:
где – модуль действующего значения тока i–ой ветви.
где – эквивалентное реактивное сопротивление i–ой ветви.
При выполнении условия баланса мощностей:
Примеры расчёта цепей однофазного синусоидального тока
Пример 6.1
| Дано: , , , Определить токи в ветвях, составить и рассчитать баланс мощностей для схемы на рис. 6.1. |
| Рис. 6.1 |
Решение
Для расчёта будем использовать метод контурных токов.
Значение контурного тока принимаем равным величине источника тока . Уравнение составляем для контурного тока :
Выражаем ток из предыдущего уравнения:
Ток в третьей ветви равен контурному току , . Запишем этот ток в показательной форме комплексного числа:
Ток во второй ветви определим как алгебраическую сумму контурных токов, проходящих через данную ветвь:
Полная мощность приёмников определяется по формуле:
Активную мощность приёмников в данной схеме определим по следующей формуле:
Реактивную мощность приёмников определяем по формуле:
Полная мощность, выделяемая в систему источниками, определяется по формуле:
Выполнение баланса мощностей подтверждает правильность решения задачи.
Пример 6.2
| Рис. 6.2 | Дано: , , , , , . Для схемы на рис. 6.2 рассчитать ток в неразветвлённой части схемы. Записать . |
Решение
Записываем функцию времени в виде показательной формы комплексного числа:
Определяем входное сопротивление схемы относительно зажимов источника напряжения:
Мгновенное значение тока имеет вид:
Пример 6.3
Рассчитать токи , , в схеме примера 6.2 графоаналитическим методом, построить топографическую диаграмму напряжений, совмещённую с векторной диаграммой токов.
Решение
Графоаналитический метод расчёта – это совокупность графического метода и метода пропорционального пересчёта. Метод основан на линейной зависимости между токами и напряжениями. Поэтому векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения, питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения. На диаграмме изменятся лишь масштабы напряжений и токов.
| Обозначим токи на схеме. Выберем масштабы: масштаб для тока ; масштаб для напряжения . Построение начинаем из точки, соответствующей отрицательной полярности входных зажимов, это точка «е » (рис. 6.3). |
| Рис. 6.3 |
Принимаем действующее значение тока . Откладываем вектор в горизонтальном направлении (рис. 6.4).
Токи и напряжения, определённые с помощью диаграммы, будем обозначать одним штрихом.
Определяем по законуОма для действующих значений напряжения на участках « » и « » цепи.
Строим вектора данных напряжений. Участок « » содержит ёмкость, напряжение на нём отстаёт от тока на , участок « » – резистивный – его напряжение совпадает с током по фазе. Концы векторов напряжений обозначаем соответствующими буквами.
Сумма векторов и определяет вектор напряжения на участке «c
–
e
». Из диаграммы по масштабу определяем величину напряжения Далее по закону Ома для участка с резистором определяем ток . Вектор тока строим с учётом масштаба из конца вектора , учитывая, что совпадает по фазе с напряжением . Сумма векторов и даёт вектор тока в общей ветви цепи: . По диаграмме определяем действующее значение . Теперь определяем действующие значения напряжений и . Строим вектор из точки С. Напряжение опережает ток на , т.к. участок « » – индуктивный, напряжение совпадает по фазе с током , т.к. участок « » содержит активное сопротивление.
Мощность в цепи постоянного тока
Здравствуйте! Эту статью можно считать началом знакомства с электричеством. Напряжение, ток, сопротивление – это три главные величины, на которых построены основные законы электротехники и эти величины связаны между собой еще одной – мощностью. А чтобы было проще знакомиться с электротехникой, мы будем рассматривать мощность в цепи постоянного тока. Дело в том, что при расчетах в цепях переменного тока появляется довольно много условий. Впрочем, обо всём по порядку и вы сейчас сами с этим разберётесь.
Для удобства я сразу напишу международные обозначения этих четырёх величин:
U – напряжение (В, вольт)
R – сопротивление (Ом, ом)
P – мощность (Вт, ватт – не надо путать с вольтом, который обозначается только одной буквой В)
Для начала абстрактный пример, чтобы проще было понимать термины, которые я сейчас буду использовать. Допустим, есть магазин товаров (условно это можно представить, как напряжение), есть деньги (условно это будет ток), есть совесть, которая не позволяет вам тратить много или наоборот, шепчет, чтобы вы крупно потратились (это можно считать сопротивлением) и есть купленные товары или продукты, которые вы несёте домой (это мощность). Собственно, на этом примере можно объяснить многие законы, связанные с электрическим током. Все обозначенные величины связаны между собой законом Ома, который гласит, что сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению цепи, а именно:
В абстрактном примере – чем больше магазин (напряжение) и чем меньше вам шепчет совесть (сопротивление), тем больше вы тратите денег (сила тока), а когда вы несёте купленный товар домой, вы совершаете работу (мощность). Мощность в цепи постоянного тока это и есть работа, совершаемая электричеством. Мощность это произведение тока на напряжение, а если вместо тока или напряжения подставить соответствующие значения, то можно получить мнемоническую табличку:
Как видите, мощность в цепи постоянного тока это довольно простое понятие, если немного вдуматься в материал. По сути, это всего две формулы с заменой значений. Как это выглядит:
Если теперь в формуле мощности подставить место значения тока формулу тока, то получим следующее:
Именно таким образом и получилось 12 формул на основе закона Ома, которые вы видите в мнемонической табличке. Что такое мощность в цепях постоянного тока мы более или менее разобрались, но есть ещё один момент.
Общее понятие
Электрическое напряжение определяется как отношение работы поля по переброске пробного заряда из одной заданной точки в другую к размеру потенциала. При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.
В переменной электрической цепи выделяется 3 вида мощности:
- активный P;
- реактивный Q;
- полного типа S.
В цепи переменного электричества формула для расчета постоянного тока применяется только для вычисления мгновенной мощности. Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.
Коэффициент скорости преобразования
Мощностной коэффициент является показателем потребления тока при присутствии реактивного компонента и искажающей нагрузки. Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.
Коэффициент равняется отношению расходуемой нагрузки к ее полному значению. При этом работа совершается за счет активного вида преобразования. При синусоидальном токе и вольтаже полная нагрузка находится в виде суммы реактивной и активной форм. Активная нагрузка приравнивается к усредненному произведению силы тока и напряжения и не может быть выше произведения аналогичных среднеквадратических размерностей. Мощностной коэффициент показывается в диапазоне от 0 до 1 или ставится в процентах от 0 до 100.
Как составить баланс мощностей
Закон сохранения энергии гласит, что энергия никуда не пропадает. Она только меняет один вид на иной, сберегая свое число. Закон объективен и для электрических цепей, следственно энергия, отдаваемая источниками, равна энергии, потребляемой в резистивных сопротивлениях. Отсель вытекает равенство выражений мощностей источников и мощностей в сопротивлениях, которое называют уравнением равновесия мощностей. Составление этого уравнения значимая задача, разрешающая проверить правильность расчетов токов и напряжений в электрической цепи
Инструкция
1. Определите мощности всех источников электрической цепи. Мощность, отдаваемая источниками напряжения Ри = ЕI, где Е – действующее значение ЭДС источника, а I – значение тока, происходящее через данный источник.
2. Обнаружьте алгебраическую сумму мощностей отдаваемых источниками. Если действительное (правильное) направление тока через источник совпадает с направлением ЭДС, то мощность такого источника позитивная. Если направление тока через источник противоположно направлению ЭДС, то мощность такого источника негативная. Для нахождения алгебраической суммы мощностей, сложите правильные мощности и от полученной суммы отнимите все негативные мощности источников.
3. Определите мощности в резистивных сопротивлениях. Мощность в резистивном сопротивлении Рн = (I^2)*R, где I – ток в резисторе, R – его сопротивление. Мощность в резисторе неизменно является позитивной, от того что мощность, затрачиваемая на нагрев, не зависит от направления тока.
4. Обнаружьте арифметическую сумму мощностей, рассеиваемых в резистивных сопротивлениях цепи. Для нахождения этой суммы сложите обнаруженные значения мощностей, потребляемых на всем резисторе.
5. Сравните сумму мощностей, отдаваемых источниками с суммой мощностей, потребляемых сопротивлениями. Если электрическая схема рассчитана верно, оба значения полученных сумм будут равны между собой. Исполнено условие равновесия. Полученное равенство – уравнение равновесия мощностей для заданной электрической схемы.
Полезный совет При расчете равновесия мощностей, источник с произвольной формой напряжения требуется заменять источником непрерывного напряжения.
Источник статьи: https://jprosto.ru/kak-sostavit-balans-moschnostey/
Практическое применение и коррекция
Если к розетке с синусоидальным напряжением 50 Гц и 230 В подсоединить нагрузку с опережением или отставанием тока от напряжения на какую-то угловую величину, то на активной внутренней катушке будет создаваться увеличенная мощность. Это значит, что при работе в таких условиях выделяется много тепла, и электростанция отводит его в увеличенном количестве, по сравнению с применением активной нагрузки.
Коэффициенты полезного действия и мощности отличаются друг от друга. Мощностной показатель не влияет на потребление приемника, подключенного к сети, но изменяет энергетические потери в подводных проводах и местах выработки энергии или ее преобразования. В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.
КПД влияет на потребляемую активную нагрузку. Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.
Коррекция заключается в приведении потребления прибора с низким мощностным коэффициентом к стандартным показателям при питании от силовой цепи переменного тока. Технически это осуществляется применением действенной схемы на входном устройстве, которая помогает равномерно использовать фазную мощность и исключает перегрузку нулевого провода. При этом снижаются всплески потребительского тока на верхушке синусоиды питающего вольтажа.
Реактивная нагрузка корректируется при включении в магистраль элемента с обратным действием. Например, в двигателе переменного тока для компенсации действия ставится конденсатор параллельно питающей линии. Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.
Источник
Погрешность в балансе мощностей
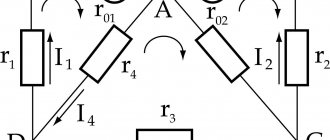
Сделал расчёт по методу контурных токов. Направление контурных токов совпадает с направлением обхода контуров.
Нашёл контурные токи: I22 = 1,83 А I33 = 2,59 А I44 = -0,57 А
Вопрос: правдиво ли выглядит?
Нужно посчитать погрешность измерений (по примеру). Мне не ясно из примера как нашли погрешность Нужно посчитать погрешность измерений.(по примеру) Мне не ясно из примера как нашли погрешность.
Задача о балансе оборудования После завершения литья в литейном цехе отливка должна перенесена в цех, где происходит ее.
не достаточно денег на балансе # Делаем ставку if (isset($_POST) and isset($_POST) and isset($_POST))
Денег на балансе нет а интернэт есть! Вообщем уехал в дургой город переустановил там винду,попользовался местной сетью(пароль вводить там.
Сообщение от Gambit_88
OldFedor
, Взялся за расчёт по методу узловых потенциалов относительно узла D. Получил довольно отличные от рассчитанных ранее токи. Собственная проводимость: GAA = 1/R2 + 1/R3 = 0,17 GBB = 1/R2 + 1/R4 + 1/R5 = 0,246 GCC = 1/R4 + 1/R6 = 0,15 Общая проводимость: GAB = GBA = -1/R2 = -0,076 GAC = GCA = 0 GBC = GCB = -1/R4 = -0,076 Узловые токи: JAA = -E2/R2 + J1 = -0,03 JBB = E2/R2 = 3,03 Здесь вопрос: JCC = или 0 — J1, т.е.
-3
?
Добавлено через 32 минуты
Пробовал оба значения, но результаты в обоих случаях далековаты:
| I1 | I2 | I3 | I4 | I5 | I6 | I7 | |
| 3 | 2,29 | 0,72 | -0,65 | 1,64 | 0,66 | 1,2 | |
| -3 | 3 | 2,65 | 0,35 | -1,84 | 0,81 | -1,18 | 15,62 |
Добавлено через 10 минут
I1 = J1 I2 = (фA — фB + E2) / R2 I3 = (фA — фD) / R3 I4 = (фC — фB) / R4 I5 = (фB — фD) / R5 I6 = (фC — фD) / R6 I7 = фD — фC + E7
И, естетственно, баланс при таком тоже далёк от посчитанного выше.
Источник