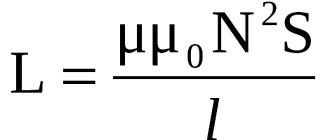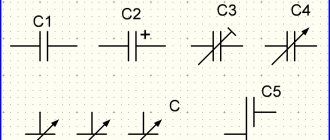Конденсатор в цепи переменного тока
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC..
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC..=Umaxcos.ωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcos.ωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsin.ωt=CUmaxcos.(ωt+π2..)
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2.. (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω..=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Определение
I=UXC..
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
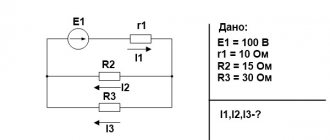
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C..=LI2max2..
Отсюда:
LC=q2maxI2max..
√LC=qmaxImax..
T=2π√LC=2πqmaxImax..=2·3,1410−610−3..≈6,3·10−3 (с)
Формулы вычисления тока в конденсаторе
Ёмкость конденсатора, включенного в цепь переменного тока, рассчитывается по формуле: C = q / U, где:
- С — ёмкость;
- q — заряд одной из пластин;
- U — напряжение внутри.
Ёмкость
Конденсаторы бывают разной формы, поэтому и их расчёт осуществляется по нескольким формулам:
- плоский — C = E × E0 × S / d;
- цилиндрический — С=2 π × E × E0 × l / ln(R2 / R1);
- сферический — C = 4 π ×E × E0 × R1 × R2 / R2 — R.
Обратите внимание! Сопротивление в переменной цепи, которое может оказывать резистор, включённый в электрическую цепь, вычислить нельзя, так как она считается бесконечно большим. Однако в данном случае, это можно сделать по формуле: Хс = 1 / 2πvC = 1 / wC.
Вам это будет интересно Магнитный пускатель
Напряжение конденсатора в цепи переменного тока вычисляется по следующей формуле: Wp = qd E / 2.
Напряжение рассчитывается по определенной формуле
Чтобы рассчитать напряжение на конденсаторе в цепи переменного тока, необходимо воспользоваться актуальными формулами.
Катушка индуктивности в цепи переменного тока
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля →Ei, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля →Eк, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства →Ei=−→Eк следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции ei) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
ei=−u
Напомним, что сила переменного тока изменяется по гармоническому закону:
i=Imaxsin.ωt
Тогда ЭДС самоиндукции равна:
ei=−Li´=−LωImaxcos.ωt
Так как u=−ei, то напряжение на концах катушки оказывается равным:
u= LωImaxcos.ωt=LωImaxsin.(ωt+π2..)=Umax(ωt+π2..)
Амплитуда напряжения равна:
Umax=LωImax
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π2.., или колебания силы тока отстают от колебаний напряжения на π2.., что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Imax=UmaxLω..
Введем обозначение:
Lω=XL
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Определение
I=UXL..
Величина XL, равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлениемXL=500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока Imax в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
XL=Lω=2πνL
Отсюда:
Так как амплитуда напряжения связана с его действующим значением соотношением Umax=U√2, то для амплитуды силы тока получаем:
Принцип работы конденсатора
Подключение прибора к постоянному источнику приводит к тому, что в начальный момент происходит аккумуляция в обкладках из-за электростатической индукции, а сопротивление в этот момент приравнивается нулю. Электрическая индукция провоцирует поле к притяжению разноимённых зарядов на разные обкладки, расположенные друг напротив друга.
Вам это будет интересно Классы автоматических выключателей
Такое свойство получило название ёмкость, которая характерна для всех типов материалов, в том числе и диэлектриков, однако в случае с проводниками она существенно больше. Именно поэтому обкладки изготавливаются из проводника. Увеличение ёмкости способствует накоплению большего количества зарядок на обкладках.
Важно! Когда аккумулируются заряды, происходят ослабление поля и наращивание двухполюсника.
Принцип работы
Происходит это из-за уменьшения места в обкладках, воздействия одноимённых зарядов друг на друга. Одновременно с этим напряжение приравнивается к источнику тока. Прекращение электричества в цепи происходит после того, когда обкладки полностью заполнятся электричеством. Из-за этого пропадает индукция и остаётся только поле, удерживающее и не пропускающее заряды.
Диэлектрик между обкладками
Электротоку будет некуда деться, а на двухполюснике напряжение приравнивается к ЭДС. Когда ЭДС повышается, поле сильнее воздействует на диэлектрик из-за отсутствия места в обкладках. Если внутреннее конденсаторное напряжение будет выше предельных значений, тогда пробьёт диэлектрик.
Конденсатор преобразуется в проводник, и происходит освобождение зарядов, из-за чего электроток начинает идти. Чтобы применять двухполюсник при высоком напряжении повышают размер диэлектрика и наращивают расстояние, имеющееся между обкладками на фоне снижения ёмкости. Диэлектрик располагается между обкладками и не даёт проходить постоянному, выполняя в отношении него барьерную функцию.
Электрическая индукция
Обратите внимание! Именно постоянное напряжение способно формировать электростатическую индукцию, но только в случае замыкания в момент зарядки конденсатора. Благодаря этому механизму сохраняется энергия до момента подсоединения к нему потребителю.
Конденсатор в цепи постоянного тока
Чтобы понять, как работает накопитель в цепи постоянного тока, надо добавить в схему лампочку, которая станет загораться только при зарядке, в процессе которой от электротока остаётся напряжение, как бы догоняющее его из-за плавного нарастания. Заряды электричества затрачивают какое-то время для перемещения к обкладкам, именно это и есть время зарядки, продолжительность которого определяется частотой и ёмкостью напряжения. Когда зарядка завершается, лампочка тухнет, и постоянный электроток перестаёт проходить через пассивный электронный компонент.
Конденсатор в цепи переменного тока
Если у источника изменить полярность, то это приведёт к разрядке конденсатора в цепи переменного тока и его повторной зарядке. Формируется постоянная электростатическая индукция при переменном. Всегда при изменении электричеством своего направления запускается механизм зарядки и разрядки, из-за чего он и пропускает переменный. Увеличение частоты приводит к снижению ёмкостного сопротивления двухполюсника.
Вам это будет интересно ДИФ или УЗО
Конденсатор в постоянной цепи
§51. Индуктивность в цепи переменного тока
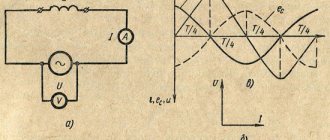
Ток, напряжение и э. д. с. самоиндукции. При включении в цепь пременного тока индуктивности (катушки индуктивности, потерями в которой можно пренебречь) (рис. 178, а) изменяющийся ток непрерывно индуцирует в ней э. д. с. самоиндукции
eL = -L ?i / ?t (68)
где ?i/?t— скорость изменения тока.
Рассматривая график изменения силы тока i (рис. 178,б), можно установить, что скорость его изменения ?i/?t будет наибольшей в моменты времени, когда угол ? равен 0; 180 и 360°. Следовательно, в эти минуты времени э. д. с. имеет наибольшее значение. В моменты времени, когда угол ?t равен 90° и 270°, скорость изменения тока ?i/?t = 0 и поэтому э. д. с. eL = 0.
Э. д. с. самоиндукции е согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. Поэтому в первую четверть периода, когда ток i увеличивается, э. д. с. eL имеет отрицательное значение (направлена против тока); во вторую четверть периода, когда ток i уменьшается, э. д. с. eL имеет положительное значение (совпадает по направлению с током). В третью четверть периода ток i изменяет свое направление и увеличивается, поэтому э. д. с. самоиндукции eL направлена против тока и имеет положительное значение. В четвертую четверть периода ток i уменьшается и э. д. с. самоиндукции eL стремится поддержать прежнее направление тока, т. е. имеет отрицательное значение. Таким образом, э. д. с. самоиндукции eL отстает по фазе от тока i на угол 90°.
Так как в цепи, куда включена индуктивность L, отсутствует активное сопротивление (рассматривается идеальная катушка индуктивности), то по второму закону Кирхгофа u+eL=0, т. е. u = -eL Следовательно, напряжение источника всегда равно по величине и противоположно по направлению э. д. с. самоиндукции.
Из рассмотрения кривых (см. рис. 178,б) видно, что кривая напряжения и сдвинута относительно кривой силы тока i на четверть периода, т. е. на угол 90°. При этом напряжение достигает наибольших и нулевых значений раньше, чем ток. Следовательно,
Рис. 178. Схема включения в цепь переменного тока индуктивности (а), кривые тока I, напряжения и, э.д.с. eL (б) и векторная диаграмма (в)
при включении в цепь переменного тока индуктивности ток i отстает по фазе от напряжения и на угол 90° или, что то же самое, напряжение и опережает ток по фазе на угол 90° (рис. 178, в).
Индуктивное сопротивление. Сопротивление катушки или проводника переменному току, вызванное действием э. д. с. самоиндукции, называется индуктивным сопротивлением. Оно обозначается XL и измеряется в омах. Физическая природа индуктивного сопротивления совершенно другая, чем активного. Э. д. с. самоиндукции eL направлена против приложенного напряжения u, которое заставляет изменяться ток; согласно закону Ленца она препятствует изменению тока i, т. е. оказывает прохождению переменного тока определенное сопротивление.
Чем большая э. д. с. самоиндукции eL индуцируется в проводнике (катушке), тем большее они имеют индуктивное сопротивление XL. Э. д. с. самоиндукции согласно формуле (68) прямо пропорциональна индуктивности L и скорости изменения тока ?i/?t, т. е. частоте его изменения f (значению ?). Поэтому индуктивное сопротивление
XL = ?L
Следовательно, индуктивное сопротивление не зависит от материала, из которого изготовлен проводник (катушка), и от площади поперечного сечения проводника.
Закон Ома для цепи с индуктивностью
I = U / xL = U / (?L)
Электрическая мощность. Рассмотрим, как изменяется электрическая мощность в цепи переменного тока с индуктивностью. Мгновенное значение мощности р, равное произведению мгновенных значений силы тока i и напряжения и, можно получить графическим путем, перемножая ординаты кривых тока и напряжения при различных углах ?t. Кривая мгновенной мощности р (рис. 179, а) представляет собой синусоиду, которая изменяется с двойной частотой 2? по сравнению с частотой изменения тока i и напряжения и.
При рассмотрении этой кривой видно, что мощность р может иметь положительные и отрицательные значения. В течение первой четверти периода ток и напряжение положительны и мощность p = ui также положительна. Во второй четверти периода ток положителен, а напряжение отрицательно; следовательно, мощность р будет отрицательна. В течение третьей четверти периода мощность снова становится положительной, а в течение четвертой четверти — отрицательной.
Понятие положительной и отрицательной электрической мощности физически определяет направление потока энергии. Положительный знак мощности означает, что электрическая энергия W передается от источника к приемнику; отрицательный знак мощности означает, что электрическая энергия W переходит от приемника к источнику. Следовательно, при включении в цепь переменного тока индуктивности возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью, при котором не создается никакой работы. В первую и третью четверти периода мощность положительна, т. е. индуктивность получает энергию W от источника (см. стрелки W) и накапливает ее в своем магнитном поле. Во вторую и четвертую четверти периода индуктивность отдает накопленную энергию W источнику. При этом протекание по цепи тока поддерживается благодаря действию э.д. с. самоиндукции eL.
Таким образом, в целом за период в индуктивное сопротивление не поступает электрическая энергия (на это указывает то, что среднее значение мощности за период равно нулю). Для того чтобы подчеркнуть указанную особенность индуктивного сопротивления, его относят к группе реактивных сопротивлений, т. е. сопротивлений, которые в цепи переменного тока в целом за период не потребляют электрической энергии. Следует отметить, что в реальные катушки индуктивности поступает некоторая энергия от источника переменного тока из-за наличия активного сопротивления проводов, из которых выполнены эти катушки. Эта энергия превращается в тепло.
Рис. 179. Кривые тока i, напряжения u и мощности р при включении в цепь переменного тока катушки индуктивности (а) и конденсатора (б)
Рис. 180. Последовательное (а) и параллельное (б) соединения катушек индуктивности
Так как среднее значение мощности в цепи с индуктивностью равно нулю, для характеристики процесса обмена энергией между источником и индуктивностью введено понятие реактивной мощности индуктивности:
QL = ULI
где UL — напряжение, приложенное к индуктивности L (действующее значение).
Реактивная мощность измеряется в варах (вар) и киловарах (квар). Наименование единицы происходит от первых букв слов вольт-амперреактивный. Реактивную мощность можно выразить также в виде
QL = U2L/XLили QL = I2XL
Способы соединения катушек индуктивности. В цепях переменного тока приходится соединять катушки индуктивности последовательно и параллельно. При последовательном соединении катушек индуктивности эквивалентная индуктивность Lэк равна сумме индуктивностей; например, при трех катушках с индуктивностями L1, L2 и L3 (рис. 180, а)
Lэк = L1+ L2 + L3
В этом случае эквивалентное индуктивное сопротивление
XLэк = XL1+ XL2 + XL3
При параллельном соединении катушек индуктивности (рис. 180,б) для эквивалентной индуктивности имеем:
1 /Lэк = 1 /L1 + 1 /L2 + 1 /L3
для эквивалентного индуктивного сопротивления
1 /XLэк = 1 /XL1 + 1 /XL2 + 1 /XL3