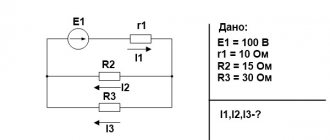
Формулы емкости конденсаторов
Для любого конденсатора справедлива формула:
где C – емкость конденсатора; q – величина заряда одной из обкладок конденсатора; – разность потенциалов между его обкладками.
Емкость конденсатора, между пластинами которого находится диэлектрик (C) (диэлектрическая проницаемость которого равна в раз больше, чем емкость такого же воздушного конденсатора ( ):
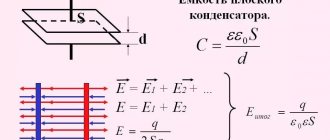
Для расчета емкости плоского конденсатора применяют формулу:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Емкость плоского конденсатора, содержащего N слоев диэлектрика (толщина i-го слоя равна , диэлектрическая проницаемость i-го слоя , определяется как:
Электрическая емкость цилиндрического конденсатора вычисляют как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Емкость сферического (шарового) конденсатора находят по формуле:
где – радиусы обкладок конденсатора.
Что такое ESR?
ESR — Equivalent Series Resistance — один из параметров конденсатора, характеризующий его активные потери в цепи переменного тока. В эквиваленте его можно представить, как включенный последовательно с конденсатором резистор, сопротивление которого определяется, главным образом, диэлектрическими потерями, а так же сопротивлением обкладок, внутренних контактных соединений и выводов. В русскоязычной аббревиатуре — Эквивалентное Последовательное Сопротивление — ЭПС.
Потери в диэлектрике, обусловленные особенностями его поляризации, составляют основную часть потерь в конденсаторе и определяются материалом, а так же толщиной слоя диэлектрика.
Поляризация — ограниченное смещение связанных зарядов диэлектрика в электрическом поле.
Рассматривать детально процессы всех видов поляризации здесь нет необходимости, но вкратце это можно пояснить следующим образом: Частицы диэлектрика, обладающие зарядом, под воздействием переменного электрического поля вынуждены совершать непроизвольные механические колебания, обусловленные их переориентацией и смещением (поляризацией). В слоях диэлектрика, близких к обкладкам, заряды, не покидая своих связей, активно участвуют во всех процессах формирования напряжения и тока в конденсаторе, как и проводники. По сути, уменьшается толщина слоя реального диэлектрика. В результате существенно повышается ёмкость конденсатора но, по причине инертности и внутреннего трения связанных частиц, процессы сопровождаются выделением тепла и потерями энергии в токопроводящих слоях диэлектрика. То есть, эти поляризованные слои обладают активным сопротивлением электрическому току. С увеличением частоты, диэлектрические потери пропорционально возрастают по той же причине — механической инертности поляризованных зарядов.
Сопротивление токопроводящих слоёв диэлектрика последовательно складывается с сопротивлением обкладок, выводов и контактных соединений. В итоге образуется общее активное сопротивление R
— Equivalent Series Resistance (ESR). По сути оно представляет собой резистор, включенный последовательно с конденсатором.
В этом случае угол сдвига фаз между током и напряжением будет не 90°, как в идеальном конденсаторе, а несколько меньше. Тангенс угла δ
, составляющего эту разницу с 90°, называют тангенсом угла потерь.
Тангенс угла определится отношением активного сопротивления к реактивному R/Xc
, как тригонометрическая функция отношения двух катетов треугольника сопротивлений, показанного на рисунке выше.
В электролитических конденсаторах значимой частью ESR является сопротивление жидкого электролита, который используется в качестве одной из обкладок для обеспечения максимальной площади соприкосновения с диэлектриком. Активное сопротивление электролита в реальных конденсаторах обычно соизмеримо с десятыми или даже с сотыми долями Ома при 20°C, но для конденсаторов большой ёмкости, используемых в фильтрах выпрямителей ИИП на рабочей частоте порядка 100 кГц, когда его реактивное сопротивление измеряется тысячными долями Ома, эта величина может составлять основные потери, и будет значительно уменьшаться по мере прогрева. При рабочей температуре величина диэлектрических потерь на таких частотах обычно оказывается в несколько раз больше.
Сопротивление электролита зависит от температуры по причине изменения степени его вязкости и подвижности ионов.
В процессе работы происходит нагрев диэлектрика и электролита переменным током, в связи с чем существенно уменьшается сопротивление электролита, тогда ESR конденсатора будет определяться преимущественно его диэлектрическими потерями, которые продолжат греть конденсатор в допустимых расчётами пределах. Но, в случаях разогрева до температуры кипения, электролит утрачивает свои первоначальные свойства и при последующем охлаждении становится более вязким, что ухудшает подвижность ионов и повышает активное сопротивление. Дальнейшая эксплуатация будет вызывать ещё больший разогрев и ухудшение качества электролита, что в последствии приведёт к непригодности конденсатора для дальнейшей работы. Неисправные конденсаторы, в которых кипел электролит, обычно определяются визуально по вздувшемуся и разгерметизированному корпусу.
Для надёжности работы электролитических конденсаторов очень важен правильный выбор его типа, номинала и максимального напряжения в зависимости от режимов и условий эксплуатации. Для фильтров выпрямителей в преобразователях, работающих на частотах десятков или сотен килогерц, производители выпускают специальные конденсаторы с малым ESR и указывают полное сопротивление переменному току (импеданс Z) для всех номиналов в таблицах. Тип таких конденсаторов сопровождается пометкой в технической документации — Low impedance или Low ESR.
Для анализа состояния электролита и внутренних соединений электролитических конденсаторов применяются измерители или пробники ESR, которые могут быть выполнены исходя из разных принципов измерений и требований к погрешностям. Большая часть простых ESR-пробников и тестеров основана на принципе измерения импеданса. У них есть свой существенный плюс — низкоомный вход, что позволяет проверять конденсаторы, не выпаивая их из платы. Подробнее о способах измерения можно ознакомиться на страничке — измерение ESR.
Наряду с ухудшением качества электролита, часто активное сопротивление в конденсаторах возрастает по причине ухудшения контактов обкладок с выводами, вплоть до полного обрыва. В электролитических это происходит чаще, в металлокерамических реже, телевизионным мастерам все эти случаи хорошо знакомы. А ремонтники старшего поколения, кто застал советские ламповые телевизоры, хорошо помнят бумажные конденсаторы, которые иногда поджимали пассатижами для уплотнения контактных соединений внутри, и они какое-то время ещё работали.
Для чего нужна таблица? Большинство пробников и тестеров, обычно светодиодные или стрелочные, измеряют импеданс — общее сопротивление конденсатора (активное и реактивное). Активное отдельно замерить сложнее, но оно и есть потери — значение ESR. При измерении ёмкостей менее 100 микрофарад, реактивная составляющая уже оказывается соизмеримой, а иногда больше значения ESR, и существенно влияет на результат. А в конденсаторах менее 10 мкф и вовсе значение ESR во много раз меньше и его доля незначительна в общем показании. Точно замерить ESR у них невозможно такими пробниками, но выявить неисправные конденсаторы можно. Другими словами, реактивное сопротивление в показаниях таких приборов — неудобная погрешность, зависимая от ёмкости конденсатора. Её надо учитывать при оценке качества конденсатора для разных ёмкостей. К тому же ESR зависит от толщины слоя электролита и диэлектрика. Для высоковольтных и крупногабаритных конденсаторов эти значения учитываются производителями в зависимости от области применения. Никакой пропорциональной зависимости ESR от других параметров конденсатора не существует, поэтому для оценки его качества в практике используются таблицы.
Все существующие таблицы — условны и не всегда объективно определяют допустимые значения для всех измерителей. Публикуют их часто для популяризации сайтов, поэтому важно понимать суть значений в таблицах. Тем более, разные пробники работают на разных принципах или частотах (от 10 до 100 кГц), разница показаний в 5 или 10 раз может отличаться от табличных лишь по этой причине. Очень полезно самому замерить значения ESR у новых конденсаторов разных производителей и составить свою таблицу для своего пробника. Это уже будут реальные показатели. Тогда их можно сравнить с неисправными конденсаторами и со значениями их реактивных сопротивлений, чтоб сделать какие-то выводы о критичности. В преобразователях блоков питания греют конденсатор паразитные десятые, иногда сотые доли Ома и, если их сможет показать Ваш измеритель, уже неплохо. Импульсный ток в конденсаторах достигает десятков Ампер и активные десятые доли Ома для 10 Ампер — это уже реальные Ватты — нагрев. Габариты конденсатора тоже имеют существенное значение, они будут охлаждать электролит, это надо учитывать при выборе типа конденсатора в мощных преобразователях. Практика показала, тонкие конденсаторы Low ESR, установленные при замене в блоках питания вместо крупногабаритных обычных, частенько долго там не живут, перегреваются, закипают и вздуваются иногда уже через несколько месяцев работы.
Для самого популярного в ИИП конденсатора 1000мкф x 25в часто в таблицах указывают 0.08 Ом, как норму. А в других таблицах 0.8 Ом. Какой прибор что мерит, кто и для каких цепей определил ему норму — загадки. Проверьте для сравнения своим прибором этот конденсатор новый от разных производителей, в том числе с пометкой Low ESR, тогда оценка будет объективнее.
Таблица Боба Паркера для ESR-метра K7214
| uF\V | 10V | 16V | 25V | 35V | 50V | 160V | 250V |
| 1 uF | 14 | 16 | 18 | 20 | |||
| 2.2 uF | 6 | 8 | 10 | 10 | 10 | ||
| 4.7 uF | 15 | 7.5 | 4.2 | 2.3 | 5 | ||
| 10 uF | 6 | 4 | 3.5 | 2.4 | 3 | 5 | |
| 22uF | 5.4 | 3.6 | 2.1 | 1.5 | 1.5 | 1.5 | 3 |
| 47 uF | 2.2 | 1.6 | 1.2 | 0.5 | 0.5 | 0.7 | 0.8 |
| 100 uF | 1.2 | 0.7 | 0.32 | 0.32 | 0.3 | 0.15 | 0.8 |
| 220 uF | 0.6 | 0.33 | 0.23 | 0.17 | 0.16 | 0.09 | 0.5 |
| 470 uF | 0.24 | 0.2 | 0.15 | 0.1 | 0.1 | 0.1 | 0.3 |
| 1000 uF | 0.12 | 0.1 | 0.08 | 0.07 | 0.05 | 0.06 | |
| 4700 uF | 0.23 | 0.2 | 0.12 | 0.06 | 0.06 |
Рассчитаем округлённо реактивное сопротивление для популярных номиналов при усреднённой частоте пробников 20 кГц, чтобы иметь представление хотя бы о порядке их идеальных значений.
Ещё раз напомню, никакой пропорции между ESR и этими значениями быть не может. Тем более, с учётом конструктивных особенностей электролитических конденсаторов для разных габаритов и вольтажа. Повторюсь. Это лишь реактивное сопротивление, которое имеет большее
значение при измерении конденсаторов
меньшей
ёмкости, как реальная погрешность для пробников, основанных на измерении импеданса. То есть, чистое значение ESR у конденсатора 100 мкф и 1 мкф может быть одинаковым, а прибор покажет разницу в десятки раз, ибо добавит ёмкостное значение, которое будет решающим для показаний прибора на измеряемой частоте у малых ёмкостей.
Реактивное сопротивление конденсаторов, частота 20кГц: 1000 мкф — 0.008 Ом. 470 мкф — 0.017 Ом. 220 мкф — 0.036 Ом. 100 мкф — 0.08 Ом. 47 мкф — 0.17 Ом. 22 мкф — 0.36 Ом. 10 мкф — 0.8 Ом. 4.7 мкф — 1.7 Ом. 2.2 мкф — 3.6 Ом. 1 мкф — 8 Ом. 0.47 мкф — 17 Ом. Поможет калькулятор расчёта реактивного сопротивления конденсаторов.
Более сложные цифровые приборы способны замерить точные значения во время заряда конденсатора постоянным током, рассчитать его ёмкость и ESR без реактивной составляющей. Но измерение постоянным током не учитывает диэлектрические потери, которые напрямую зависят от частоты. Кроме того, конденсаторы нужно выпаивать из платы для таких замеров.
Пробниками обычно быстро проверяют конденсаторы на неисправность, не выпаивая их, а это существенный выигрыш в оперативности для мастера — ремонтника. Ему не всегда нужны точные показания сложных приборов, чаще бывает важно своевременно и правильно выявить неисправную деталь в устройстве. К погрешностям на реактивность в практике мастера просто привыкают, когда годами пользуются одним и тем же пробником.
Спасибо за внимание!
Замечания и предложения принимаются и приветствуются!
Что такое конденсатор?
Конденсатор состоит из двух проводящих пластин, расположенных очень близко друг к другу и разделённых диэлектриком. Применение постоянного напряжения к пластинам вызовет протекание тока и появление на обеих крышках одинаковых по модулю, но противоположных по знаку зарядов: отрицательных – на одной и положительных – на другой. Отключение источника питания приведёт к тому, что заряд не исчезнет моментально, игнорируя явление его постепенной утечки. Затем, если крышки детали подключены к какой-то нагрузке, например, к вспышке, конденсатор разрядится сам и вернёт всю накопленную в нём энергию во вспышку.
Обозначение конденсаторов
Конденсаторы – это пассивные компоненты, которые хранят электрический заряд. Эта простая функция применяется в различных случаях:
- При переменном токе.
- При постоянном токе.
- В аналоговых сетях.
- В цифровых цепях.
Примеры использования приборов: системы синхронизации, формирование сигнала, связь, фильтрация и сглаживание сигнала, настройка телевизоров и радиоприёмников.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
- Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Измерение сопротивления конденсаторов.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Сопротивление конденсатора.
Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.
Советуем изучить Антенна для автомагнитолыПротиводействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.
Вся энергия затрачиваемая источником тока на преодоление емкостного сопротивления превращается в энергию электрического поля конденсатора. Когда конденсатор будет разряжаться вся энергия электрического поля вернется обратно в цепь в виде энергии электрического тока. Таким образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.
Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?
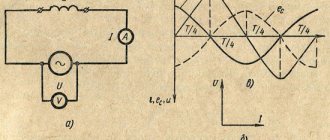
Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.
А теперь замкнем цепь переменного тока. В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.
В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора. В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.
Одновременная поляризация огромного количества атомов образует ток, называемый током смещения.
Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.
конденсатора определяется по формуле
На активном сопротивлении напряжение U акт и ток I совпадают по фазе. На емкостном сопротивлении напряжение U c отстает от тока I на 90 0 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 0 .
Формула емкости цилиндрического конденсатора
Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой. Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:
Здесь видим несколько новых переменных:
- l – высота цилиндра;
- R1 и R2 – радиус первого и второго (внешнего) цилиндров;
- ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.
Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).
Из нее видно, что все расстояния нужно приводить к метру.
Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.
Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.
При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.
График, отображающий эту величину конденсатора при непостоянном токе цепи, имеет форму гиперболы
Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.
Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.
Сопротивление конденсатора переменному напряжению
При включении конденсатора в цепь с переменным током, ток свободно проходит через конденсатор. Это объясняется очень просто: происходит процесс постоянной зарядки и разрядки конденсатора. При этом говорят, что в цепи присутствует емкостное сопротивление конденсатора, помимо активного сопротивления.
И так, конденсатор, который включен в цепь переменного тока, ведет себя как сопротивление, то есть оказывает влияние на силу тока, текущую в цепи. Величину емкостного сопротивления обозначим как , его величина связана с частотой тока и определена формулой:
где — частота переменного тока; — угловая частота тока; C — емкость конденсатора.
Если конденсатор включен в цепь переменного тока, то в нем не затрачивается мощность, потому что фаза тока сдвинута по отношению к напряжению на . Если рассмотреть один период колебания тока в цепи (T), то происходит следующее: при заряде конденсатора (это составляет ) энергия в поле конденсатора запасается; на следующем отрезке времени () конденсатор разряжается и отдает энергию в цепь. Поэтому ёмкостное сопротивление называют реактивным (безваттным).
Следует заметить, что в каждом реальном конденсаторе реальная мощность (мощность потерь) все же тратится, при течении через него переменного тока. Это вызвано тем, что происходят изменения в состоянии диэлектрика конденсатора. Помимо этого существует некоторая утечка в изоляции обкладок конденсатора, поэтому появляется небольшое активное сопротивление, которое как бы включено параллельно конденсатору.
Как рассчитать Xc
Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.
Формула вычисления показателя напряжения за одну секунду
Формула расчета величины силы электротока за мгновение
Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:
Наибольшие величины напряженности и силы тока можно рассчитывать по формуле
Окончательная формула расчета емкостного сопротивления в цепи переменного тока
f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
О реальном конденсаторе
Реальный конденсатор имеет одновременно два сопротивления: активное и емкостное. Их следует считать включенными последовательно.
Напряжение приложенное генератором к активному сопротивлению и ток идущий по активному сопротивлению совпадают по фазе.
Советуем изучить Литий ионный аккумулятор
Напряжение приложенное генератором к емкостному сопротивлению и ток идущий по емкостному сопротивлению сдвинуты по фазе на 90 . Результирующее напряжение приложенное генератором к конденсатору можно определить по правилу параллелограмма.
На активном сопротивлении напряжение Uакт и ток I совпадают по фазе. На емкостном сопротивлении напряжение Uc отстает от тока I на 90 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 .
В чем измеряется емкостное электросопротивление
R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.
Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.
Способы соединения элементов
Монтаж изделия на плату может быть вертикальным или горизонтальным. При использовании нескольких изделий они могут быть соединены между собой разными способами.
Параллельное соединение
Для его организации нужно подключить группу деталей к электроцепи так, чтобы обкладки всех деталей были подсоединены напрямую к местам включения. Поскольку все компоненты получают заряд от одного источника тока, у них будет одинаковая разность потенциалов. Но так как заряд копится на каждом изделии отдельно, количество электричества на группе можно выразить как сумму количеств на ее деталях.
Это справедливо и для емкостных данных – значение для конфигурации равно сумме значений каждой единицы. Поэтому такую группу можно считать равной одному конденсатору, емкостной параметр которого равен сумме таковых для всех частей.
Последовательное соединение
Эта схема подразумевает соединение устройств одно за другим, когда к местам подключения к цепи подсоединены только два крайних изделия. Количество электричества для каждой детали будет одинаковым. При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.
Важно! Емкостной показатель такой системы будет еще меньше, чем у устройства, обладающего наименьшим его значением. Соотношение выглядит так: 1/С = 1/С1 + 1/С2 + 1/С3 + … Опираясь на него, можно произвести вывод непосредственно формулы С. Для двух элементов: С = С1*С2 / С1+С2.
Последовательное подключение
Смешанное соединение
Такая сложная конструкция содержит фрагменты с двумя вышеприведенными типами соединений. Чтобы подсчитать полную емкость, схему делят на простые блоки, состоящие только из деталей, соединенных каким-то одним образом. Находят эквивалентные значения для каждого блока и затем рисуют схему заново в упрощенном виде. Рассчитывают данные для получившейся системы.
Чтобы суметь подобрать подходящий конденсаторный набор, нужно уметь узнавать емкостные данные. Важно также знать, как рассчитывается показатель для конфигурации из нескольких деталей, соединенных между собой тем или иным образом.
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
- пикофарад — 10—12 Ф;
- нанофарад — 10—9 Ф;
- микрофарад — 10—6 Ф.
Вам это будет интересно Материал, из какого должен изготавливаться искусственный заземлитель
Диэлектрическая проницаемость
Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
- А — площадь меньшей пластины;
- d — расстояние между ними;
- ε — абсолютная проницаемость используемого диэлектрического материала.
Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:
- 1,0006 — воздух;
- 2,5—3,5 — бумага;
- 3—10 — стекло;
- 5—7 — слюда.
Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.
Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
Советуем изучить Заземляющий контур
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Определение энергии конденсатора
Чтобы выяснить, от чего будут зависеть накопительные характеристики, можно применить две методики. Первая – это определение работы, которая выполняется для распределения зарядов на обкладках. Подразумевается, что для этого понадобится затратить определенную энергию. Во втором варианте пользуются притяжением разноименных зарядов. Для перемещения пластин до прямого контакта нужно выполнить соответствующую работу.
Энергия поля плоского конденсатора
Как подобрать конденсатор
Для упрощения можно рассмотреть пример с перемещением разноименно заряженных пластин. Сформированная сила притяжения (F) будет измеряться величиной заряда (q) и напряженностью поля (E) между соответствующими обкладками:
F = q * E.
Так как E = q/(2*e0*S), несложно получить выражение для значения силового взаимодействия:
F = q2/(2*e0*S),
где:
- e0 – это электрическая постоянная = 8,854 * 10-12 Ф*м-1;
- S – площадь пластин.
Работа (A) равна произведению силы на пройденное расстояние (d), поэтому W (энергия плоского конденсатора) = A = F * d = d *q2/(2*e0*S). Емкость © определяется, как C = d /(e0*S). Следующими преобразованиями можно получить итоговое выражение:
- W = q2/(2*C);
- q = C * U;
- энергия конденсатора формула:
W = ½ *C * U2.
Ёмкость уединённого проводника
Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.
Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что
Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
Например, потенциал уединённого шара в вакууме равен:
где — заряд шара, — его радиус. Отсюда ёмкость шара:
(2)
Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:
Соответственно, ёмкость шара в раз увеличивается:
(3)
Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.
Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.
В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.
Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.
мкФ.
Как видите, Ф — это очень большая ёмкость.
Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):
Следовательно, диэлектрическая постоянная может измеряться в Ф/м:
Ф.
Так легче запомнить, не правда ли?
Переменный ток
Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току
. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.
Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного
сопротивления еще
резистивным
и
индуктивным
. На практике все это надо обязательно учитывать, потому что возможны ситуации (обычно связанные с ростом частоты сигнала), когда конденсатор перестает быть конденсатором и превращается… в некое подобие катушки индуктивности . При проектировании схем этот момент обязательно надо иметь в виду. Согласитесь, господа, крайне неприятно поставить в схему конденсатор и потом столкнуться с тем, что из-за высокой частоты он ведет себя и не как конденсатор вовсе, а как самый настоящий дроссель. Это, безусловно, очень важная тема, но сегодня речь пойдет не о ней. В сегодняшней статье мы будем говорить непосредственно про
емкостное
сопротивление конденсатора. То есть мы будем считать его идеальным, без каких бы то ни было паразитных параметров вроде индуктивности или активного сопротивления.
Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все (рисунок 1).
Рисунок 1 – Конденсатор в цепи переменного тока
К его обкладкам приложено некоторое переменное напряжение U(t), и через него течет некоторый ток I(t). Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока, там мы про все это довольно подробно говорили. Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так
В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом
Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов! Помните, на эту тему была отдельная статья? В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная
запись комплексного числа. Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида
то его можно представить в показательной форме вот так
Почему это так, откуда взялось, что здесь какая буковка значит – обо всем уже подробно говорили. Для повторения можно перейти по ссылке и еще раз со всем ознакомиться.
Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого
Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике. Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Давайте представим, что t=0. Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам
сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой. Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с
амплитудой
сигнала. Сейчас как раз такой момент. Поэтому полагаем
t=0 и получаем комплексную амплитуду напряжения
Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями.
Итак, у нас имеется три множителя. Будем разбираться со всеми по порядку. Объединим первые два и запишем выражение следующего вида
Что мы вообще такое записали? Правильно, комплексную амплитуду тока
через конденсатор. Теперь выражение для комплексной амплитуды напряжения принимает вид
Результат, к которому мы стремимся, уже близок, но остается еще один не очень приятный множитель с экспонентой. Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике, не зря ж я ее писал . Давайте преобразуем этот множитель, воспользовавшись формулой Эйлера:
Да, вся эта хитрая экспонента с комплексными числами в показателе превращается всего лишь в мнимую единичку, перед которой стоит знак минус. Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид
Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома. Получим
Как мы помним из статьи про закон Ома, у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение – переменные и представлены через комплексные амплитуды. Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное
сопротивление конденсатора переменному току
:
Да, выражение для сопротивления конденсатора имеет вот такой вот вид. Оно, как вы можете заметить, комплексное
. Об этом свидетельствует буковка
j в знаменателе дроби. А что значит эта комплексность? На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фазв 90 градусов
между током и напряжением на конденсаторе. А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье. Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это
j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент . Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло.
Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода? Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно.
Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения. Но она не влияет на амплитуды тока и напряжения. Соответственно, если сдвиг фаз нас не интересует
, то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:
Согласитесь, жить стало чуточку легче. Это выражение позволяет рассчитать сопротивление конденсатора для конкретной емкость и частоты сигнала. Заметьте, господа, интересный факт. Сопротивление конденсатора, оказывается, зависит не только от самого конденсатора (а именно его емкости), но и от частоты протекающего тока.
Если вспомнить обычные резисторы, то в них у нас сопротивление зависело только от самого резистора, материала, формы и всего такого прочего, но не зависело от частоты (разумеется, мы говорим сейчас про идеальные резисторы, без всяких паразитных параметров). Здесь все по-другому. Один и тот же конденсатор на разной частоте будет иметь разное сопротивление и через него будет течь ток разной амплитуды при одной и той же амплитуде напряжения.
Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора. И чем больше емкость конденсатора, тем меньше его сопротивление переменному току.
По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах. Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным
. И другое оно в первую очередь из-за того самого пресловутого
j в знаменателе, то есть из-за сдвига фазы. У «обычных» (которые называют активными
) Омов такого сдвига нет, там напряжение четко совпадает по фазе с током. Давайте построим график зависимости сопротивления конденсатора от частоты. Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ. График представлен на рисунке 2.
Рисунок 2 (кликабельно) – Зависимость сопротивления конденсатора от частоты
На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы.
При стремлении частоты к нулю
(то есть фактически при стремлении переменного току к постоянному) сопротивление конденсатора стремится к бесконечности. Это и логично: мы все помним, что для постоянного тока конденсатор фактически представляет собой разрыв цепи. На практике оно, конечно, не бесконечно, а ограничено сопротивлением утечки конденсатора. Тем не менее, оно все равно очень велико и часто его и считают бесконечно большим.
При стремлении частоты к бесконечности
, сопротивление конденсатора стремится к нулю. Это все в теории, конечно. На практике реальный конденсатор обладает рядом паразитных параметров (в частности, паразитная индуктивности и сопротивление утечки), из-за чего сопротивление уменьшается только лишь до некоторой определенной частоты, а потом начинает наоборот расти. Но об этом более подробно в другой раз.
Есть еще один вопрос, который хотелось бы обговорить, прежде чем начинать рассмотрение примеров. Зачем вообще писать букву j в знаменателе сопротивления? Не достаточно ли просто всегда помнить про сдвиг фаз, а в записи использовать числа без этой мнимой единицы? Оказывается, нет. Представим себе цепь, где одновременно присутствуют резистор и конденсатор. Скажем, они соединены последовательно. И вот тут-то как раз мнимая единичка рядом с емкостью не позволит просто так взять и сложить активное и реактивное сопротивление в одно действительное число. Общее сопротивление такой цепочки будет комплексным, причем состоящим как из действительной части, так и из мнимой. Действительная часть будет обусловлена резистором (активными сопротивлением), а мнимая – емкостью (реактивным сопротивлением). Впрочем, это все тема для другой статьи, сейчас не будем в это углубляться. Давайте лучше перейдем к примерам.
Пусть у нас есть конденсатор емкостью, скажем C=1 мкФ. Требуется определить его сопротивление на частоте f1=50 Гц и на частоте f2=1 кГц. Кроме того, следует определить амплитуду тока с учетом того, что амплитуда приложенного к конденсатору напряжения равна Um=50 В. Ну и построить графики напряжения и тока.
Собственно, задачка эта элементарная. Подставляем циферки в формулу для сопротивления и получаем для частоты f1=50 Гц сопротивление, равное
А для частоты f2=1 кГц сопротивление будет
По закону Ома находим величину амплитуды тока для частоты f1=50 Гц
Аналогично для второй частоты f2=1 кГц
Теперь мы легко можем записать законы изменения тока и напряжения, а также построить графики для этих двух случаев. Полагаем, что напряжение у нас изменяется по закону синуса для первой частоты f1=50 Гц следующим образом
А для второй частоты f2=1 кГц вот так
Дальше мы помним, что ток в конденсаторе опережает напряжение на .
Поэтому с учетом этого можем записать закон изменения тока через конденсаторы для первой частоты
f1=50 Гц
и для частоты f2=1 кГц
Графики тока и напряжения для частоты f1=50 Гц представлены на рисунке 3
Рисунок 3 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f1=50 Гц
Графики тока и напряжения для частоты f2=1 кГц представлены на рисунке 4
Рисунок 4 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f2=1 кГц
Итак, господа, мы сегодня познакомились с таким понятием, как сопротивление конденсатора переменному току, научились его считать и закрепили полученные знания парочкой примеров. На сегодня все. Спасибо что прочитали, всем огромной удачи и пока!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Social button for Joomla