Внутреннее сопротивление источника постоянного тока формула

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

заменяются участки провода, не отвечающие требованиям по диаметру сечения;
перекручиваются болтовые соединения с обязательной установкой врезных шайб;
вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
при необходимости в контур защитного заземления добавляются дополнительные элементы;
исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Закон Ома для полной цепи

Учтем, что основную работу совершают сторонние силы внутри источника тока. Ее величина равна произведению заряда, переносимого полем, и электродвижущей силы источника:

q · E = I2 ·(r + R) · t.

понимая, что заряд равен произведению силы тока на время его протекания, имеем:

E = I · (r + R).

В соответствии с причинно-следственными связями закон Ома имеет вид:

I = E : (r + R).

Сила тока в замкнутой цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна общему (полному) сопротивлению цепи.

Опираясь на эту закономерность, можно определить и внутреннее сопротивление источника тока.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

где:

r – внутреннее сопротивление источника;
ε – ЭДС источника;
I – сила тока в полной цепи;
R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Нахождение внутреннего сопротивления[править]

Расчётправить

Понятие расчёт

применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).

Пусть, имеется двухполюсник, который может быть описан приведенной выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

ЭДС генератора напряжения U
Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1

) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

\( \begin{matrix} U_{out1} = U — r I_1 \\ U_{out2} = U — r I_2 \end{matrix} \)

(1)

где Uout1

— выходное напряжение при токе
I1
,
Uout2
— выходное напряжение при токе
I2
. Решая систему уравнений, находим искомые неизвестные:

\( r = \frac {U_{out1} — U_{out2}} {I_2 — I_1}, \quad U = U_{out1} + I_1 \frac {U_{out1} — U_{out2}} {I_2 — I_1} = U_{out1} + I_1 r \)

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (1) записывается следующим образом:

\( \begin{matrix} U_{oc} = U — 0 \\ 0 = U — r I_{sc} \end{matrix} \)

где Uoc

— выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки;
Isc
— ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

\( r = \frac {U_{oc}} {I_{sc}}, \quad U = U_{oc} \)

(2)

Таким образом, чтобы расчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:

Расчитать выходное напряжение двухполюсника в режиме холостого хода
Расчитать выходной ток двухполюсника в режиме короткого замыкания
На основании полученных значений найти r
и
U
по формуле (2).

Измерениеправить

Понятие измерение

применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчета — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощенной формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Часто применяется следующий простой способ измерения, не требующий вычислений:

Измеряется напряжение холостого хода
В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нем составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивлениеправить

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет

реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.

Измерение

реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:

Можно искать различные параметры комплексного значения: модуль, , только или часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость
от частоты, то есть провести измерения на
всех
частотах, которые может генерировать источник данного двухполюсника.

Реактивное внутреннее сопротивление

Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.

Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.

На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.

Что такое внутреннее сопротивление

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.
В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для гальванического элемента или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

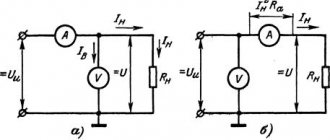
На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены ЭДС источника, его внутреннее сопротивление, а также сопротивление нагрузки. Согласно закону Ома для замкнутой цепи, ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен току короткого замыкания. Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

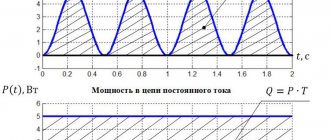
Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает источник:

Ясно, что если источник развивает такую мощность, что на нагрузке получается максимум возможной мощности для данного источника, то КПД источника окажется равным 50%.

Источник

Большое внутреннее сопротивление

Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.

Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.

Внутреннее сопротивление источника ЭДС

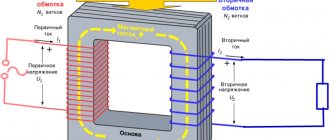
Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.

Выглядит все это в аккумуляторе примерно вот так:

Итак, что у нас получается в чистом виде?

Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Влияние внутреннего сопротивления на свойства двухполюсника

Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:

где:

E – напряжение ЭДС;
R – сопротивление нагрузки;
r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.

Сложности использования

В принципе, любая из возможных окислительно-восстановительных реакций может быть использована в батареях. Но веществ, способных работать в ценных технически элементах, не так уж и много. Более того, многие реакции требуют затрат дорогостоящих веществ.

Современные аккумуляторные батареи имеют более простое строение. Два электрода, помещенные в один электролит, заполняют сосуд – корпус батареи. Такие конструктивные особенности упрощают строение и удешевляют аккумуляторы.

Любой гальванический элемент способен создавать постоянный ток.

Сопротивление тока не позволяет всем ионам одновременно оказаться на электродах, поэтому элемент работает достаточно долго. Химические реакции образования ионов рано или поздно прекращаются, элемент разряжается.

Внутреннее сопротивление источника тока имеет большое значение.

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Радиосвязь

ЭДС и напряжение. Внутреннее сопротивление источников питания.Ликбез так ликбез! Закон Ома. Вот я о чем. О законе Ома мы уже говорили. Поговорим еще раз — с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. ( электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток. Переведя сие заклинание на язык сухих формул получаем:

I=E/R

где:I — сила тока,E — Э.Д.С. — электродвижущая силаR — сопротивление Ток измеряется в амперах, э.д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):

I=U/R

где:U — напряжение источника непосредственно на его клеммах. Рассмотрим простой пример. Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое — то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э.д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.Но, тем не менее именно эта величина и принимается за напряжение батарейки. Формула конечного напряжения при этом будет иметь следующий вид:

U(бат)=E-U(внутр)

Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу! Разобрались! Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер. Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться — к просадке напруги. Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму. Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.

Видео

Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Расчет внутреннего сопротивления источника напряжения

Реальные источники напряжения обладают собственным электрическим сопротивлением, которое называется «внутреннее сопротивление». Присоединенная на выводы источника нагрузка обозначается под названием «внешнее сопротивление» – R.

Батарея аккумуляторов генерирует ЭДС:

ε = E/Q, где:

Е – энергия (Дж);
Q – заряд (Кл).

Суммарная ЭДС аккумуляторного элемента является напряжением его разомкнутой цепи при отсутствии нагрузки. Его можно проконтролировать с хорошей точностью цифровым мультиметром. Разность потенциалов, измеренная на выходных контактах батареи, когда она включена на нагрузочный резистор, составит меньшую величину, чем ее напряжение при незамкнутой цепи, по причине протекания тока через нагрузочное внешнее и через внутреннее сопротивление источника, это приводит к рассеиванию энергии в нем как теплового излучения.

Внутреннее сопротивление аккумулятора с химическим принципом действия находится между долей ома и несколькими омами и в основном связано с сопротивлением электролитических материалов, используемых при изготовлении батареи.

Если резистор сопротивлением R подсоединить к батарее, ток в цепи I = ε/(R + r).

Внутреннее сопротивление – не постоянная величина. На него влияет род батареи (щелочная, свинцово-кислотная и т. д.), оно изменяется в зависимости от нагрузочного значения, температуры и срока использования аккумулятора. К примеру, у разовых батареек внутреннее сопротивление возрастает во время использования, а напряжение в связи с этим падает до прихода в состояние, непригодное для дальнейшей эксплуатации.

Если ЭДС источника – заранее данная величина, внутреннее сопротивление источника определяется, измеряя ток, протекающий через нагрузочное сопротивление.

Так как внутреннее и внешнее сопротивление в приближённой схеме включены последовательно, можно использовать законы Ома и Кирхгофа для применения формулы:

Из этого выражения r = ε/I — R.

Пример.

Аккумулятор с известной ЭДС ε = 1.5 В и соединен последовательно с лампочкой. Падение напряжения на лампочке составляет 1,2 В. Следовательно, внутреннее сопротивление элемента создает падение напряжения: 1,5 — 1,2 = 0,3 В. Сопротивление проводов в цепи считается пренебрежимо малым, сопротивление лампы не известно. Измеренный ток, проходящий через цепь: I = 0,3 А. Нужно определить внутреннее сопротивление аккумулятора.

По закону Ома сопротивление лампочки R = U/I = 1,2/0,3 = 4 Ом;
Теперь по формуле для расчета внутреннего сопротивления r = ε/I — R = 1,5/0,3 — 4 = 1 Ом.

В случае короткого замыкания внешнее сопротивление падает почти до нуля. Ток может ограничивать свое значение только маленьким сопротивлением источника. Сила тока, возникающая в такой ситуации, настолько велика, что источник напряжения может быть поврежден тепловым воздействием тока, существует опасность возгорания. Риск пожара предотвращается установкой предохранителей, например, в цепях автомобильных аккумуляторов.

Внутреннее сопротивление источника напряжения – важный фактор, когда решается вопрос, как передать наиболее эффективную мощность подсоединенному электроприбору.

Важно!

Максимальная передача мощности происходит, когда внутреннее сопротивление источника равно сопротивлению нагрузки.

Однако при этом условии, помня формулу Р = I² x R, идентичное количество энергии отдается нагрузке и рассеивается в самом источнике, а его КПД составляет всего 50%.

Требования нагрузки должны быть тщательно рассмотрены для принятия решения о наилучшем использовании источника. Например, свинцово-кислотная автомобильная батарея должна обеспечивать высокие токи при сравнительно низком напряжении 12 В. Ее низкое внутреннее сопротивление позволяет ей это делать.

В некоторых случаях источники питания высокого напряжения должны иметь чрезвычайно большое внутреннее сопротивление, чтобы ограничить ток к. з.

Измерение сопротивления петли фаза-нуль

заменяются участки провода, не отвечающие требованиям по диаметру сечения;
перекручиваются болтовые соединения с обязательной установкой врезных шайб;
вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
при необходимости в контур защитного заземления добавляются дополнительные элементы;
исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Внешнее и внутреннее сопротивление

Сопротивление нагрузки, в данном случае лампочки, соединенной с источником тока, носит название внешнего сопротивления. Непосредственное сопротивление источника тока называется внутренним сопротивлением. Для более наглядного изображения процесса, все значения необходимо условно обозначить. I – сила тока, R – внешнее сопротивление, r – внутреннее сопротивление. Когда по электрической цепи протекает ток, то для того, чтобы поддерживать его, между концами внешней цепи должна присутствовать разность потенциалов, которая имеет значение IхR.

Но, протекание тока наблюдается и во внутренней цепи. Значит, для того, чтобы поддержать электроток во внутренней цепи, также необходима разность потенциалов на концах сопротивления r. Значение этой разности потенциалов равно Iхr.

Реактивное внутреннее сопротивление

Внутреннее сопротивление — формула

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Большое внутреннее сопротивление

Работа тока

В соответствии с законом Джоуля-Ленца в проводниках выделяется количество теплоты, пропорциональное сопротивлению. Если количество теплоты обозначить Qвнут., силу тока I, время его протекания t, то получим:

Qвнут. = I2 ·r · t,

где r – внутреннее сопротивление источника тока.

Во всей цепи, включающей как внутреннюю, так и внешнюю ее части, выделится полное количество теплоты, формула которого имеет вид:

Qполное = I2 ·r · t + I2 ·R · t = I2 ·(r +R) ·t,

Известно, как обозначается сопротивление в физике: внешняя цепь (все элементы, кроме источника) имеет сопротивление R.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

цепи, содержащие источник тока или напряжения;
двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

Чему равно внутреннее сопротивление идеального источника тока

Как и в случае идеальных пассивных элементов, при идеализации активных элементов (источник напряжения, источник тока) на них накладывают энергетические ограничения. Первое ограничение заключается в том, что в идеальных активных элементах не происходит ни рассеяния, ни накопления электрической энергии. Второе ограничение состоит в том, что идеальные активные элементы обладают неограниченной мощностью, которую они могут отдавать в электрическую цепь.

Идеальным источником напряжения называют активный элемент, напряжение на зажимах которого не зависит от параметров цепи, подключенной к нему, т.е. не зависит от величины тока, протекающего через источник.

Условное графическое обозначение идеального источника напряжения показано на рис.1.15. Его выполняют в виде окружности (обычно диаметром 8 мм), внутри которой располагается стрелка, указывающая положительное направление ЭДС

. На зажимах источника возникает напряжение .

Рис. 1.15. Условное графическое изображение идеального источника напряжения

В соответствии с определением идеального источника напряжения, он имеет внутреннее сопротивление

и обладает бесконечной мощностью. Так, если сопротивление нагрузки на зажимах источника ,то его ток ( ), а напряжение источника остается равным , что и приводит к бесконечно большой величине мощности , которой не может обладать реальный источник напряжения.

Идеальным источником тока называется идеализированный активный элемент, ток которого не зависит от напряжения на его зажимах. Условное обозначение идеального источника тока показано на рис.1.16. Двойная стрелка (рис. 1.16,а) показывает направление тока внутри источника.

В соответствии с определением идеального источника тока, он обладает бесконечной мощностью и имеет внутреннее сопротивление

. Так, если сопротивление нагрузки

(рис. 1.16,б) неограниченно увеличивать (

), то по определению, через нее должен проходить ток
i,
создавая на зажимах напряжение и мощность будет неограниченно увеличиваться ( ).

Рис. 1.16. Идеальный источник тока:

а – условное графическое изображение;

Влияние внутреннего сопротивления на свойства двухполюсника

где:

E – напряжение ЭДС;
R – сопротивление нагрузки;
r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

Сопротивление

Внутреннее сопротивление источника тока и противодействие внешней части цепи имеют несколько различную природу, но одинаковым в этих процессах является совершение работы по перемещению заряда.

Сама работа зависит только от свойств источника и его наполнения: качеств электродов и электролита, так же как для внешних частей цепи, сопротивление которых зависит от геометрических параметров и химических характеристик материала. К примеру, сопротивление металлического провода возрастает с увеличением его длины и уменьшается при расширении площади сечения. При решении задачи, как уменьшить сопротивление, физика рекомендует использовать специализированные материалы.

Разрядная емкость источника

Как проявляется внутреннее сопротивление

Личин у него очень много. Вот некоторые из них.

Прокрастинация и самосаботаж

Вот сейчас пройду ещё пару квестов в «Ведьмаке» и точно примусь за диплом. Да, я помню, что дедлайн завтра и, если я ничего не сдам, меня могут отчислить. Но всё равно буду играть до ночи и сяду за работу в самый последний момент. Если вообще сяду.

Избегание и откладывание

Надо бы подтянуть английский, чтобы меня повысили. Но сейчас и так много дел. Вот разгребу их все и тогда сразу займусь изучением языка. И вообще, давайте не будем пока об этом.

Перфекционизм

Если я буду писать книгу, то она должна быть гениальной — такой, чтобы сразу номинировали на «Букера». Нет, на Нобелевку. И чтобы напечатали миллионным тиражом и в первый же день восхищённые читатели всё скупили. Что? Так не получится? Ну тогда я и писать ничего не буду.

Инертность и поиск оправданий

Хотел установить на телефон приложение для домашних тренировок, но оно, оказывается, платное. 500 рублей в месяц как‑то жалко. Можно, конечно, бесплатные найти, но это искать, выбирать, смотреть… Нет, как‑нибудь в другой раз потренируюсь.

Занудство

Хочу пройти курсы интернет‑маркетинга, но вот в первой школе нет раздела про контекстную рекламу, во второй обучение на 10 тысяч дороже, а в третьей у преподавателя страница в Facebook какая‑то неубедительная. И вообще, вдруг я не справлюсь или работу потом не найду. Наверное, стоит ещё раз всё хорошенько обдумать, взвесить за и против, составить сравнительную таблицу — и тогда я, может быть, решусь.

Пессимизм

Хочется эмигрировать, но это так долго, сложно и дорого. Уверен, что ничего у меня всё равно не получится, так что лучше и не пытаться.

Отрицание и защита

Я тут подумал и понял, что мне на самом деле не нужно менять работу. Зарплата стабильная, соцпакет какой‑никакой. Сейчас кризис, лучше сидеть в тепле и не высовываться. Роста нет? Это не главное, я уже о нём не переживаю.

Самокритика

Что это ты удумал? На танцы пойти? Посмотри на себя, ты же деревянный, музыку не слышишь, в ритм не попадаешь. Какие тебе танцы, не смеши людей — пойди лучше полы помой.

Страхи и блоки

Смотрю на чистый лист и не знаю, что нарисовать. Вдруг нарисую что‑то, а получится ерунда, за которую меня раскритикуют.

Калькулятор внутреннего сопротивления источника тока

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

Калькулятор внутреннего сопротивления источника тока

Для участка цепи, справедлива формула, позволяющая связать величины силы тока, напряжения и сопротивление участка цепи:

U — напряжение на участке цепи
I — ток на участке цепи
R — сопротивление участка цепи

Из этой формулы также выводятся формулы для нахождения напряжения и сопротивления цепи:

Закон Ома для полной цепи

Как вы наверное знаете, в полной цепи напряжение на выходе батарейки или генератора или другого источника питания не постоянно, а зависит от нагрузки: чем больше нагрузка, тем ниже будет напряжение на выходе.

Для расчёта полных цепей применяется закон Ома для полной цепи:

, где:

ε — Э.Д.С. источника тока. Его можно найти, если измерить напряжение на выходе источника без нагрузки.
r — внутреннее сопротивление источника тока.

Источник