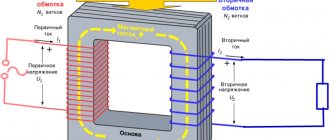
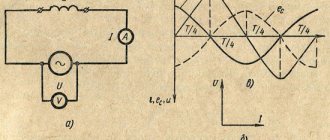
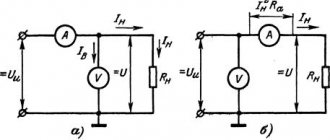
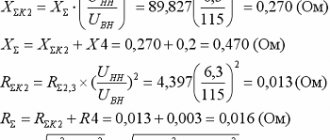Внешняя характеристика источника ЭДС
Внешняя характеристика отражает зависимость напряжения на зажимах источника от величины нагрузки — тока источника, заданного нагрузкой. Напряжение на зажимах источника меньше ЭДС на величину падения напряжения на внутреннем сопротивлении источника (1):
Этому уравнению соответствует внешняя характеристика источника ЭДС (рис. 1). построенная по двум точкам:
Очевидно, что напряжение на зажимах источника ЭДС тем больше, чем меньше его внутреннее сопротивление.
В идеальном источнике ЭДС R0=0, U=E (напряжение не зависит от величины нагрузки). Однако не всегда при анализе и расчете цепи источник электрической энергии удобно представлять в качестве источника ЭДС. Если внутреннее сопротивление источника значительно превышает внешнее сопротивление цепи, что, например, имеет место в электронике, то получим, что ток в цепи I=U/(R+R0) и при R0>>R практически не зависит от сопротивления нагрузки. В этом случае источник энергии представляют в качестве источника тока.
Разделим уравнение (1) на R0 (2):
Уравнению (2) соответствует схема замещения, приведенная на рис. 2. Здесь Iв=U/R0 и Ik=E/R0, I= Ik — Iв тогда (3)
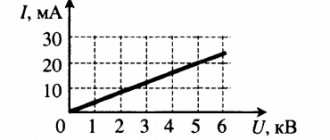
Для идеального источника тока Rс = ∞. Вольтамперные характеристики реального и идеального источников тока показаны на рис. 3.
Когда нет четкого разграничения величин R и R0 , в качестве расчетного эквивалента источника энергии можно использовать либо источник ЭДС, либо источник тока. В последнем, случае для определения падения напряжения используют выражение (3).
Режимы работы источника
Источник может работать в следующих режимах:
1. Номинальный режим — это режим работы, на который рассчитан источник заводом-изготовителем. Для данного режима в паспорте источника указывают номинальные ток Iном и номинальное напряжение Uном или мощность Pном.
2. Режим холостого хода. В этом режиме внешняя цепь отключена от источника, ток источника I = 0 и, следовательно, напряжение на зажимах источника — напряжение холостого хода Uхх = Е — см. уравнение (1).
3. Режим короткого замыкания. Сопротивление внешней по отношению к источнику цепи равно нулю. Ток источника ограничивается только его внутренним сопротивлением. Из уравнения (1) при U=0 получаем I = Iкз = U / R0. Для уменьшения потерь энергии в источнике ЭДС R0 должно быть возможно меньшим, а в идеальном источнике R0 = 0. С учетом этого Iкз >> Iном и является недопустимым для источника.
Источники электрической энергии. Внешняя характеристика
к оглавлению
В цепях переменного тока, также как в цепях постоянного, должны действовать источники электрической энергии. Отличие этих источников заключается лишь в том, что создаваемые ими ЭДС или токи являются синусоидальными функциями времени.
Источники делятся на идеальные и реальные
. У идеальных источников отсутствует внутреннее сопротивление или проводимость. Создаваемые ими ЭДС или ток определяются только параметрами источника.
В электрической цепи с идеальными источниками величина тока через источник ЭДС или напряжение на источнике тока определяются нагрузкой
.
На электрических схемах они изображаются точно также как источники постоянного тока, но стрелки в условном обозначении указывают направление принятое
за положительное.
Реальные источники электрической энергии имеют внутреннее сопротивление Z
или проводимость
Y
(рис. 1). Однако на переменном токе эти величины в общем случае являются
комплексными
.
Также как на постоянном токе, реальный источник может быть представлен двумя эквивалентными схемами с источником ЭДС или с источником тока. Внутреннее сопротивление, проводимость и параметры источников связаны между собой отношениями
| Y = 1/ | (1) |
формально идентичными соответствующим выражениям для источников постоянного тока. ЭДС и ток внутренних источников соответствуют напряжению на выходе в режиме холостого хода и току в режиме короткого замыкания.
ЗАДАЧА 1
Для источников переменного тока невозможно построить вольтамперную характеристику. Ее роль играет внешняя характеристика
, т.е
зависимость действующего значения напряжения на выходе источника от величины действующего значения тока в нагрузке, при постоянном значении угла сдвига фаз в нагрузке j
н
.
Рассмотрим электрическую цепь, состоящую из реального источника и нагрузки общего вида (рис. 2). Ток в нагрузке по закону Ома можно определить из выражения
| . | (2) |
Отсюда, падение напряжения в нагрузке
| , | (3) |
где — комплексное относительное сопротивление нагрузки
.
Падение напряжения в нагрузке можно представить в относительных единицах, если выбрать в качестве базовой величины ЭДС источника. Тогда комплексное относительное напряжение в нагрузке
из выражения (3) будет —
| . | (4) |
Ток в цепи также можно представить в относительных единицах, если в качестве базовой величины выбрать ток короткого замыкания источника I
кз=
E
/
Zs
. Отсюда
комплексный относительный ток —
| . | (5) |
Модуль комплексного относительного тока или просто относительный ток можно получить, определив модуль знаменателя выражения (5) из выражения для комплексного относительного сопротивления, в виде
| . | (6) |
Из выражения (2) с учетом (6) относительное напряжение в нагрузке будет
| . | (7) |
Выражения (6) и (7) позволяют построить внешнюю характеристику источника
электрической энергии в относительных единицах, если в них принять в качестве переменной модуль комплексного относительного сопротивления нагрузки z , при условии постоянства его аргумента d .
Внешние характеристики для относительного сопротивления нагрузки, изменяющегося в пределах 0 < z <�µ , при четырех значениях разности углов φ нагрузки и внутреннего сопротивления источника построены на рис. 3. Использование относительных единиц позволяет анализировать закономерности функций безотносительно конкретных значений параметров. Любой источник электрической энергии в режиме холостого хода имеет выходное напряжение равное ЭДС внутреннего источника, а в режиме короткого замыкания, ток на выходе равен току внутреннего источника тока. Любой реальный источник обладает также конечным значением внутреннего сопротивления, что позволяет соотнести его с сопротивлением нагрузки и получить для нагрузочного сопротивления, изменяющегося в диапазоне от нуля до бесконечности, изменение относительного сопротивления z в том же диапазоне. Поэтому выбор указанных значений в качестве базовых для относительных единиц позволяет распространить выводы из анализа внешних характеристик на любой реальный источник при всех возможных вариантах нагрузки.
Из выражений (6) и (7) следует, что при определенных условиях относительное напряжение нагрузки и ток могут иметь значение больше единицы. Это означает, что в нагрузке может протекать ток больше тока короткого замыкания
источника и существовать напряжение
больше ЭДС источника
. Определим эти условия.
Для относительного тока i условие i > 1.0 сводится к условию , а для относительного напряжения u — к условию — . Отсюда для тока и напряжения получим соответственно условия
| и | (8) |
| . | (9) |
Так как 0 < z <�µ , то соотношения (8) и (9) будут выполняться только для
|d | >p /2
, если же это условие выполнено, то всегда найдутся такие значения z , при которых эти выражения будут справедливыми
. Это означает, что внешняя характеристика будет иметь участки, на которых напряжение в нагрузке превышает ЭДС источника и ток в нагрузке превышает ток короткого замыкания.
Аргумент комплексного относительного сопротивления d представляет разность φ н
-φ
s
Но т.к. обе величины по абсолютному значению меньше p /2, то условие |d | > p /2 может быть выполнено только, если реактивные составляющие комплексных сопротивлений нагрузки и источника имеют противоположные знаки.
Таким образом, из выражений (8) и (9) можно определить диапазоны относительных сопротивлений, при которых относительный ток и напряжение будут больше единицы в виде
| 0 < z < — 2cosd и | (10) |
| . | (11) |
Если z одновременно находится в диапазонах, определяемых выражениями (10) и (11), то внешняя характеристика имеет участок, на котором обе относительные величины (ток и напряжение) больше единицы. Для этого границы обоих диапазонов должны перекрываться. Определим значение d, для предельного состояния, когда границы диапазонов совпадают, т.е. 2cosd = 1/(2cosd). Отсюда d = 3p /2.
Рассмотрим вопрос о полной или кажущейся мощности в нагрузке. Эта величина не имеет такого физического смысла как активная и реактивная мощность, но с ее помощью можно оценить предельно возможную мощность устройства. Полная мощность представляет собой произведение тока и напряжения, поэтому из выражений (6) и(7) ее можно записать в относительных единицах в виде
| . | (12) |
Проверим выражение (12) на наличие экстремума. Для этого возьмем производную ds
/
dz
и приравняем ее нулю. Экстремум существует, является максимумом и соответствует z = 1.0 . Подставив это значение относительного сопротивления в (7), получим уравнение геометрического места точек экстремума на плоскости внешней характеристики — u = i , т.е. все точки максимальной полной мощности располагаются на линии, проходящей через начало координат под углом 45° .
Значение максимальной полной мощности из (12) получается подстановкой z = 1.0 —
| . | (13) |
Из выражения (13) следует, что максимальная полная мощность минимальна и равна 1/4, когда аргументы комплексных сопротивлений нагрузки и источника одинаковы. По мере роста разности φ н
-φ
s
мощность быстро растет и стремится к бесконечности, когда φ
н
= -φ
s
= ± p /2. Физически это объясняется тем, что в этих условиях
Zs
+
Z
н= 0 и ток возрастает до бесконечно большого значения (см. выражение (2)). Реально такой режим в системе источник-нагрузка невозможен, однако на практике относительная полная мощность может быть существенно больше единицы.
Из проведенного анализа внешних характеристик реальных источников электрической энергии можно сделать следующие выводы:
- внешние характеристики
- если реактивные составляющие
комплексного сопротивления нагрузки и комплексного сопротивления источника питания различны по характеру, то в системе источник-нагрузка
возможны режимы, когда напряжение на нагрузке превышает ЭДС источника и ток нагрузки превышает ток короткого замыкания
; - если |φ н
— φ
s
| > p /2, то
существуют диапазоны нагрузок, в пределах которых падение напряжения на нагрузке превышает ЭДС источника или ток в нагрузке превышает ток короткого замыкания
; - если |φ н
-φ
s
| > 3p /2, то
существует диапазон нагрузок, в пределах которого одновременно падение напряжения на нагрузке превышает ЭДС источника и ток в нагрузке превышает ток короткого замыкания
; - максимальная полная мощность в нагрузке соответствует условию равенства модуля ее комплексного сопротивления модулю внутреннего сопротивления источника;
- значение максимальной полной мощности определяется только разностью
источника переменного тока в общем случае нелинейны
; исключением является характеристика, соответствующая равенству аргументов комплексного сопротивления нагрузки φни внутреннего комплексного сопротивления источника φs(d =0);
|φ н
-φ
s
|.
ЗАДАЧА 2
к оглавлению
Знаете ли Вы,
что релятивизм (СТО и ОТО) не является истинной наукой? — Истинная наука обязательно опирается на причинность и законы природы, данные нам в физических явлениях (фактах). В отличие от этого СТО и ОТО построены на аксиоматических постулатах, то есть принципиально недоказуемых догматах, в которые обязаны верить последователи этих учений. То есть релятивизм есть форма религии, культа, раздуваемого политической машиной мифического авторитета Эйнштейна и верных его последователей, возводимых в ранг святых от релятивистской физики. Подробнее читайте в FAQ по эфирной физике.
Источник ЭДС. Идеальный и реальный источники.
Источник ЭДС это активный элемент цепи, который имеет два вывода. Напряжение на этих выводах не зависит от сопротивления цепи, в которую он включен. То есть независимо от того какой ток будет создавать источник ЭДС в цепи напряжение на его выводах не изменится.
Считается, что внутри источника ЭДС отсутствуют пассивные элементы, такие как активное сопротивление, индуктивность и емкость. То есть можно сказать, что внутренне сопротивление источника ЭДС равно нулю.
Как всем известно, в пассивных элементах схемы ток протекает от большего потенциала к меньшему. В источнике ЭДС процесс идет в обратном направлении. Внутренние силы источника будь то химические как в батарейке или механические как в динамо машине совершают работу по перемещению зарядов от отрицательного полюса к положительному.
Идеальный источник ЭДС в природе не существует. И в правду трудно себе представить такой источник. В котором при замыкании его выводов между собой, нулевым сопротивлением, возникнет бесконечно большой ток. Это видно из закона Ома. I=U\R при R=0 получим I=U/0.
В реальных же источниках ЭДС всегда присутствует внутренне сопротивление. Таким образом, при замыкании выводов между собой падение напряжения на внутреннем сопротивлении уравновешивает ЭДС источника. Следовательно, ток короткого замыкания будет иметь какую-то конечную величину.
На схеме реальный источник обозначается как источник ЭДС с включенным последовательно сопротивлением. Его значение подбирается так чтобы отобразить поведение реального источника. Как правило, величина этого внутреннего сопротивления ничтожна, мала и может не браться в рассмотрение. Хотя все зависит от поставленной задачи и конкретной цепи.
ВАХ идеального источника ЭДС показана на рисунке 2. Как видно при изменении тока в цепи напряжение остается неизменным.
Идеальные источники тока и напряжения
2015-05-13 4369
Как и в случае идеальных пассивных элементов, при идеализации активных элементов (источник напряжения, источник тока) на них накладывают энергетические ограничения. Первое ограничение заключается в том, что в идеальных активных элементах не происходит ни рассеяния, ни накопления электрической энергии. Второе ограничение состоит в том, что идеальные активные элементы обладают неограниченной мощностью, которую они могут отдавать в электрическую цепь.
Идеальным источником напряжения называют активный элемент, напряжение на зажимах которого не зависит от параметров цепи, подключенной к нему, т.е. не зависит от величины тока, протекающего через источник.
Условное графическое обозначение идеального источника напряжения показано на рис.1.15. Его выполняют в виде окружности (обычно диаметром 8 мм), внутри которой располагается стрелка, указывающая положительное направление ЭДС . На зажимах источника возникает напряжение .
Рис. 1.15. Условное графическое изображение идеального источника напряжения
В соответствии с определением идеального источника напряжения, он имеет внутреннее сопротивление и обладает бесконечной мощностью. Так, если сопротивление нагрузки на зажимах источника ,то его ток ( ), а напряжение источника остается равным , что и приводит к бесконечно большой величине мощности , которой не может обладать реальный источник напряжения.
Идеальным источником тока называется идеализированный активный элемент, ток которого не зависит от напряжения на его зажимах. Условное обозначение идеального источника тока показано на рис.1.16. Двойная стрелка (рис. 1.16,а) показывает направление тока внутри источника.
В соответствии с определением идеального источника тока, он обладает бесконечной мощностью и имеет внутреннее сопротивление . Так, если сопротивление нагрузки
(рис. 1.16,б) неограниченно увеличивать ( ), то по определению, через нее должен проходить ток i,
создавая на зажимах напряжение и мощность будет неограниченно увеличиваться ( ).
Источник
Источник ЭДС и источник тока в электрических цепях
При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением величины внутреннего сопротивления r0 заменяют расчетным эквивалентным источником ЭДС или источником тока.
Рис. 1.14
Источник ЭДС (рис. 1.14) имеет внутреннее сопротивление r0, равное внутреннему сопротивлению реального источника. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС.
Для данной цепи запишем соотношение по второму закону Кирхгофа
(1.10)
E=U+Ir0 или E=U−Ir0.
Эта зависимость напряжения U на зажимах реального источника от тока I определяется его вольт-амперной или внешней характеристикой (рис. 1.15). Уменьшение напряжения источника U при увеличении тока нагрузки I объясняется падением напряжения на его внутреннем сопротивлении r0.
| Рис. 1.15 | Рис. 1.16 |
У идеального источника ЭДС внутреннее сопротивление r
0<<
R
н (приближенно
r
0≈0). В этом случае его вольт-амперная характеристика представляет собой прямую линию (рис. 1.16), следовательно, напряжение
U
на его зажимах постоянно (
U
=
E
) и не зависит от величины сопротивления нагрузки
R
н.
Рис. 1.17
Источник тока, заменяющий реальный источник электрической энергии, характеризуется неизменным по величине током I
к, равным току короткого замыкания источника ЭДС , и внутренним сопротивление
r
0, включенным параллельно (рис. 1.17).
Стрелка в кружке указывает положительное направление тока источника. Для данной цепи запишем соотношение по первому закону Кирхгофа
I
к=
I
0+
I
; .
В этом случае вольт-амперная (внешняя) характеристика I
(
U
) источника тока определится соотношением
(1.11)
I
=
I
к−
I
0=
I
к−
U
/
r
0
и представлена на рис. 1.18.
| Рис. 1.18 | Рис. 1.19 |
Уменьшение тока нагрузки I при увеличении напряжения U на зажимах ab источника тока, объясняется увеличением тока I0, замыкающегося в цепи источника тока.
В идеальном источнике тока r0>>Rн. В этом случае можно считать, что при изменении сопротивления нагрузки Rн потребителя I0≈0, а I≈Iк. Тогда из выражения (1.11) следует, что вольт-амперная характеристика I(U) идеального источника тока представляет прямую линию, проведенную параллельно оси абсцисс на уровне I=Iк=E/r0 (рис. 1.19).
При сравнении внешних характеристик источника ЭДС (рис. 1.15) и источника тока (рис. 1.18) следует, что они одинаково реагируют на изменение величины сопротивления нагрузки. Покажем, что в обоих случаях ток I в нагрузке определяется одинаковым соотношением.
Ток в нагрузке Rн для схем источника ЭДС (рис. 1.14) и источника тока (рис. 1.17) одинаков и равен .
Для схемы (рис. 1.14) это следует из закона Ома, т.к. при последователь-ном соединении сопротивления r0 и Rн складываются. В схеме (рис. 1.17) ток распределяется обратно пропорционально сопротивлениям r0 и Rн двух параллельных ветвей. Ток в нагрузке Rн
,
т.е. совпадает по величине с током при подключении нагрузки к источнику ЭДС. Следовательно, схема источника тока (рис. 1.17) эквивалентна схеме источника ЭДС (рис. 1.14) в отношении энергии, выделяющейся в сопротивлении нагрузки Rн, но не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания.
Каким из двух эквивалентных источников питания пользоваться, не играет существенной роли. Однако на практике, особенно при расчете электротехнических устройств, чаще используется в качестве источника питания источник ЭДС с внутренним сопротивлением r0 и величиной электродвижущей силы E.
В тех случаях, когда номинальное напряжение или номинальный ток и мощность источника электрической энергии оказываются недостаточными для питания потребителей, вместо одного используют несколько источников. Существуют два основных способа соединения источников питания: последовательное и параллельное.
Последовательное включение источников питания (источников ЭДС) применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС (рис. 1.20).
Рис. 1.20
Для этой цепи на основании второго закона Кирхгофа можно записать
E
1+
E
2+
E
3=
I
(
r
01+
r
02+
r
03+
R
н),
откуда
.
Таким образом, электрическая цепь на рис. 1.20 может быть заменена цепью с эквивалентным источником питания (рис. 1.21), имеющим ЭДС E
э и внутреннее сопротивление
r
э.
| Рис. 1.21 |
|
При параллельном соединении источников (рис. 1.22) соединяются между собой положительные выводы всех источников, а также их отрицательные выводы. Характерным для параллельного соединения является одно и то же напряжение U
на выводах всех источников. Для электрической цепи на рис. 1.22 можно записать следующие уравнения:
I
=
I
1+
I
2+
I
3;
P
=
P
1+
P
2+
P
3=
UI
1+
UI
2+
UI
3=
UI
.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников. Параллельное соединение источников применяется в первую очередь тогда, когда номинальные ток и мощность одного источника недостаточны для питания потребителей. На параллельную работу включают обычно источники с одинаковыми ЭДС, мощностями и внутренними сопротивлениями.