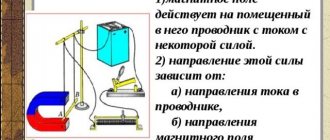
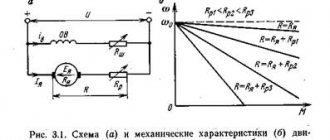
As shown earlier, one of the most important advantages of multiphase systems is the production of a rotating magnetic field using stationary coils, on which the operation of AC motors is based. Let's begin our consideration of this issue by analyzing the magnetic field of a coil with a sinusoidal current.
Magnetic field of a coil with sinusoidal current
When a sinusoidal current is passed through the coil winding, it creates
a magnetic field, the induction vector of which changes (pulsates) along this coil also according to a sinusoidal law. The instantaneous orientation of the magnetic induction vector in space depends on the winding of the coil and the instantaneous direction of the current in it and is determined by the right-hand gimlet rule. So for the case shown in Fig. 1, the magnetic induction vector is directed upward along the axis of the coil. After half a period, when at the same magnitude the current changes its sign to the opposite one, the magnetic induction vector with the same absolute value will change its orientation in space by 1800. Taking into account the above, the magnetic field of a coil with a sinusoidal current is called pulsating.
Circular rotating magnetic field of two- and three-phase windings
A circular rotating magnetic field is a field whose magnetic induction vector, without changing in magnitude, rotates in space with a constant angular frequency.
To create a circular rotating field, two conditions must be met:
- The axes of the coils must be shifted in space relative to each other by a certain angle (for a two-phase system - by 900, for a three-phase system - by 1200).
- The currents feeding the coils must be shifted in phase according to the spatial displacement of the coils.
Let's consider obtaining a circular rotating magnetic field in the case of a two-phase Tesla system (Fig. 2,a).
When harmonic currents are passed through the coils, each of them, in accordance with the above, will create a pulsating magnetic field. Vectors and characterizing these fields are directed along the axes of the corresponding coils, and their amplitudes also change according to a harmonic law. If the current in coil B lags behind the current in coil A by 900 (see Fig. 2,b), then .
Let us find the projections of the resulting magnetic induction vector on the x and y axes of the Cartesian coordinate system associated with the axes of the coils:
The module of the resulting magnetic induction vector in accordance with Fig. 2.v is equal
| , | (1) |
in this case, for the tangent of the angle a formed by this vector with the abscissa axis, we can write
,
where
| . | (2) |
The resulting relationships (1) and (2) show that the vector of the resulting magnetic field is unchanged in magnitude and rotates in space with a constant angular frequency, describing a circle, which corresponds to a circular rotating field.
Let us show that a symmetrical three-phase system of coils (see Fig. 3, a) also makes it possible to obtain a circular rotating magnetic field.
Each of the coils A, B and C, when passing harmonic currents through them, creates a pulsating magnetic field. The vector diagram in space for these fields is shown in Fig. 3, b. For projections of the resulting magnetic induction vector onto
axes of the Cartesian coordinate system, the y-axis of which is aligned with the magnetic axis of phase A, can be written
| ; | (3) |
| . | (4) |
The given relations take into account the spatial arrangement of the coils, but they are also fed by a three-phase current system with a temporary phase shift of 1200. Therefore, for the instantaneous values of the coil inductions, the relations take place
; ; .
Substituting these expressions into (3) and (4), we get:
| ; | (5) |
| (6) |
In accordance with (5) and (6) and Fig. 2.c for the magnitude of the magnetic induction vector of the resulting field of three coils with current can be written:
,
and the vector itself makes an angle a with the x-axis, for which
,
where
.
Thus, in this case, there is a constant magnetic induction vector, rotating in space with a constant angular frequency, which corresponds to a circular field.
Magnetic field in an electric machine
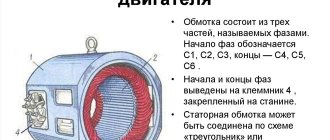
In order to strengthen and concentrate the magnetic field in an electric machine, a magnetic circuit is created for it. An electric machine consists of two main parts (see Fig. 4): a stationary stator and a rotating rotor, made respectively in the form of hollow and solid cylinders.
There are three identical windings on the stator, the magnetic axes of which are shifted along the bore of the magnetic core by 2/3 of the pole division, the value of which is determined by the expression
,
where is the radius of the magnetic core bore, and p is the number of pole pairs (the number of equivalent rotating permanent magnets creating a magnetic field - in the case shown in Fig. 4, p = 1).
In Fig. 4 solid lines (A, B and C) mark the positive directions of the pulsating magnetic fields along the axes of the windings A, B and C.
Assuming the magnetic permeability of steel to be infinitely large, let us construct a distribution curve of the magnetic induction in the air gap of the machine, created by the winding of phase A, for a certain moment t (Fig. 5). When constructing, we take into account that the curve changes abruptly at the locations of the coil sides, and in areas devoid of current, there are horizontal sections.
Let's replace this curve with a sinusoid (it should be noted that in real machines, due to the appropriate design of the phase windings for the resulting field, such a replacement is associated with very small errors). Taking the amplitude of this sinusoid for the selected time t equal to VA, we write
| (7) |
and similarly
| ; | (8) |
| . | (9) |
Taking into account harmonically varying phase currents for instantaneous values of these quantities, with the previously made assumption about the linearity of the dependence of induction on current, we can write
.
Substituting the last relations into (7)…(9), we obtain
| ; | (10) |
| ; | (11) |
| . | (12) |
Having summed up relations (10)…(12), taking into account the fact that the sum of the last terms on their right-hand sides is identically equal to zero, we obtain for the resulting field along the air gap of the machine the expression
,
which is the traveling wave equation.
Magnetic induction is constant if . Thus, if you mentally select a certain point in the air gap and move it along the magnetic core bore at a speed
,
then the magnetic induction for this point will remain unchanged. This means that over time, the magnetic induction distribution curve, without changing its shape, moves along the circumference of the stator. Therefore, the resulting magnetic field rotates at a constant speed. This speed is usually determined in revolutions per minute:
.
Operating principle of asynchronous and synchronous motors
The design of an asynchronous motor corresponds to the image in Fig. 4. The rotating magnetic field created by the current-carrying windings located on the stator interacts with the rotor currents, causing it to rotate. The most widely used currently is an asynchronous motor with a squirrel-cage rotor due to its simplicity and reliability. Current-carrying copper or aluminum rods are placed in the grooves of the rotor of such a machine. The ends of all the rods at both ends of the rotor are connected by copper or aluminum rings that short-circuit the rods. This is where the rotor got its name.
Eddy currents arise in the short-circuited rotor winding under the influence of the emf caused by the rotating field of the stator. Interacting with the field, they involve the rotor in rotation at a speed fundamentally lower than the rotation speed of the field 0. Hence the name of the motor - asynchronous.
Magnitude
called relative slip
. For standard motors S=0.02…0.07. The inequality of the speeds of the magnetic field and the rotor becomes obvious if we take into account that the rotating magnetic field will not cross the current-carrying rods of the rotor and, therefore, currents involved in the creation of rotating torque will not be induced in them.
The fundamental difference between a synchronous motor and an asynchronous one is the design of the rotor. The latter in a synchronous motor is a magnet made (at relatively low powers) on the basis of a permanent magnet or on the basis of an electromagnet. Since opposite poles of magnets attract, the rotating magnetic field of the stator, which can be interpreted as a rotating magnet, drags along the magnetic rotor, and their speeds are equal. This explains the name of the motor - synchronous.
In conclusion, we note that unlike an asynchronous motor, which usually does not exceed 0.8...0.85, with a synchronous motor it is possible to achieve a higher value and even make it so that the current will lead the voltage in phase. In this case, like capacitor banks, a synchronous machine is used to improve the power factor.
Literature
- Fundamentals
of circuit theory: Textbook. for universities / G.V. Zeveke, P.A. Ionkin, A.V. Netushil, S.V. Strakhov. –5th ed., revised. –M.: Energoatomizdat, 1989. -528 p. - Bessonov L.A.
Theoretical foundations of electrical engineering: Electric circuits. Textbook for students of electrical engineering, energy and instrument engineering specialties of universities. –7th ed., revised. and additional –M.: Higher. school, 1978. –528 p. - Theoretical
foundations of electrical engineering. Textbook for universities. In three volumes. Under general. ed. K.M.Polivanova. T.1. K.M.Polivanov. Linear electrical circuits with lumped constants. – M.: Energia- 1972. –240 p.
Control questions
- What field is called pulsating?
- What kind of field is called a rotating circular field?
- What conditions are necessary to create a circular rotating magnetic field?
- What is the operating principle of an asynchronous motor with a squirrel-cage rotor?
- What is the operating principle of a synchronous motor?
- At what synchronous speeds are general industrial AC motors produced in our country?
Tesla system for producing a rotating magnetic field
N. Tesla was one of the first to obtain a rotating magnetic field. The scientist used a two-phase system. He passed through two coils (Fig. 1), located at an angle of 90°, alternating electric currents varying according to harmonic laws. In this case, each coil created a pulsating magnetic field.
Need advice from a teacher in this subject area? Ask a question to the teacher and get an answer in 15 minutes! Ask a Question
Figure 1. Tesla's system for producing a rotating magnetic field. Author24 - online exchange of student work
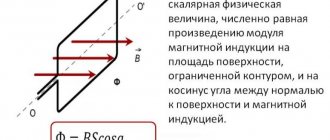
Figure 1 shows the directions of the magnetic fields that the coils create: $\vec{B}_{1}$ and $\vec{B}_{2}$. . The magnetic fields of individual coils vary according to the laws of sines, as do the currents in the coils. Let the phase shift in the oscillations of the magnitudes of the magnetic induction vectors be $\frac{\pi }{2}$:
$B_{1}=B_{m}\sin {\left( \omega t \right)\left( 1 \right),}$
$B_{2}=B_{m}\sin {\left( \omega t-\frac{\pi }{2} \right)\left( 2 \right).}$
In projections on the axes of the Cartesian coordinate system ($XOY$) in Fig. 1, equations (1) and (2) give:
$B_{1y}=B_{1}=B_{m}\sin {\left( \omega t \right)\left( 3 \right),}$
$B_{2x}=-B_{m}\sin {\left( \omega t-\frac{\pi }{2} \right)=B_{m}\cos {(\omega t)}\left( 4\right).}$
Let us find the magnitude of the resulting field using the Pythagorean theorem:
$B=\sqrt {B_{x}^{2}+B_{y}^{2}} =B_{m}\left( 5 \right)$
Expression (5) indicates that the magnitude of the resulting magnetic field does not change. From Fig. 1 it is clear that the angle that the resulting magnetic induction vector makes with the $X$ axis is equal to:
$tg\, \left( \alpha \right)=\frac{B_{1y}}{B_{1x}}=\frac{B_{m}\sin \left( \omega t \right)}{B_{ m}\cos {(\omega t)}}=tg\left( \omega t \right)\to \alpha =\omega t\left( 6 \right)$
The results shown in expressions (5) and (6) tell us that the vector of magnetic induction of the total field is constant in magnitude and rotates in space with an angular velocity $\omega=const.$ The hodograph $\vec{B}$ represents is a circle that corresponds to a rotating magnetic field; the rotation of the field is called circular.