Definition of Lorentz force
The Lorentz force is a combination of magnetic and electric force on a point charge that is caused by electromagnetic fields. Or in other words, the Lorentz force is a force acting on any charged particle that falls in a magnetic field at a certain speed. Its value depends on the magnitude of the magnetic induction B, the electric charge of the particle q and the speed with which the particle falls in the field - V. Read on to learn about the formula for calculating the Lorentz force, as well as its practical significance in physics.
Discovery of the Lorentz force
The magnetic field does not interact with charges at rest, and for a long time the connection between magnetic and electrical phenomena was not discovered. For the first time such a connection - the influence of a current-carrying conductor on a compass needle - was discovered in the first half of the 19th century. H. Oersted. The opposite phenomenon - the influence of a magnet field on a current-carrying conductor (as well as the interaction of two current-carrying conductors) - was soon discovered by A. Ampere.
Rice. 1. The effect of a magnetic field on a current-carrying conductor.
However, the mechanism of the emergence of the Ampere force was studied only towards the end of the 19th century. By this time it became clear that electric current is the ordered movement of charged particles. Therefore, the Ampere force arises due to the fact that the magnetic field exerts a force on moving charges.
Such a force was discovered by H. Lorenz. He also derived its formula.
A little history
The first attempts to describe electromagnetic force were made back in the 18th century. Scientists Henry Cavendish and Tobias Mayer proposed that the force on magnetic poles and electrically charged objects obeys the inverse square law. However, the experimental proof of this fact was not complete and convincing. It was only in 1784 that Charles Augustine de Coulomb, using his torsion balance, was able to finally prove this assumption.
In 1820, the physicist Oersted discovered the fact that a volt current acts on the magnetic needle of a compass, and Andre-Marie Ampere in the same year was able to develop a formula for the angular dependence between two current elements. In fact, these discoveries became the foundation of the modern concept of electric and magnetic fields. The concept itself was further developed in the theories of Michael Faraday, especially in his idea of lines of force. Lord Kelvin and James Maxwell added detailed mathematical descriptions to Faraday's theories. In particular, Maxwell created the so-called “Maxwell field equation” - which is a system of differential and integral equations that describe the electromagnetic field and its relationship with electric charges and currents in vacuum and continuous media.
JJ Thompson was the first physicist to try to derive from Maxwell's field equation the electromagnetic force that acts on a moving charged object. In 1881, he published his formula F = q/2 vx B. But due to some miscalculations and an incomplete description of the bias current, it turned out to be not entirely correct.
And finally, in 1895, the Dutch scientist Hendrik Lorentz derived the correct formula, which is still used today, and also bears his name, just as the force that acts on a flying particle in a magnetic field is now called the “Lorentz force.”
Hendrik Lorenz.
Using the right hand rule in electrodynamics
If you hang a frame with current in a magnetic field on a thin and flexible wire, it will rotate and be positioned in a certain way. The behavior of a magnetic needle is similar. This indicates the vector nature of the physical quantity characterizing the magnetic field. In this case, the direction of this vector will be related to the orientation of the frame and arrow. The physical vector quantity that characterizes the magnetic field is the magnetic induction vector ($\vec{B}$).
Finished works on a similar topic
- Course work Rule of left and right hands for magnetic field 480 rub.
- Abstract Left and right hand rule for magnetic field 250 rub.
- Test work Left and right hand rule for magnetic field 200 rub.
Get completed work or advice from a specialist on your educational project Find out the cost
This is one of the main parameters describing the state of the magnetic field, so you need to be able to find its magnitude and, of course, direction.
To determine the direction of the magnetic induction vector, use:
- right screw rule or
- right hand rule.
The direction of the magnetic induction vector, at the location of the frame with current, is considered to be the direction of the positive perpendicular ($\vec{n}$) to this frame. The positive normal ($\vec{n}$) will have the same direction as the direction of translational movement of the right screw if its head is rotated along the current in the frame (Fig. 1 (a)).
Figure 1. Determination of the direction of the magnetic induction vector. Author24 - online exchange of student work
Thus, having a test frame with current, placing it in the field under study, allowing it to rotate freely in it, you can determine the direction of the magnetic induction vector at each point in the field. You just need to let the frame come to a balanced position, then use the right screw rule.
Do you need proofreading or review of academic work? Ask a question to the teacher and get an answer in 15 minutes! Ask a Question
Now let's look at the right hand rule. Let's clench our right hand into a loose fist (Fig. 2). Bend your thumb 90°. Let's place the hand so that the thumb indicates the direction of current flow, then the bent other four fingers will indicate the direction of the lines of magnetic induction of the field that creates the current. And we remember that the tangent at each point of the field to the field line (magnetic induction line) indicates the direction $\vec{B}$.
Figure 2. Right hand rule. Author24 - online exchange of student work
Let's consider a solenoid. Let's clasp it with our right palm so that four fingers coincide with the direction of the current in it, then the finger bent ninety degrees will indicate the direction of the magnetic field created inside it.
We know that if a conductor is moved in a magnetic field, an induction current will arise in this conductor. The right hand rule can be used to determine the direction of flow of induced current in such conductors. Wherein:
- the magnetic field induction lines should enter the open palm of the right hand,
- bend the finger of this hand ninety degrees and direct it according to the speed of movement of the conductor,
- the extended four fingers will indicate the direction of the induction current.
The right-hand rule can be used to determine the direction of the induced emf in a circuit:
With the bent four fingers of your right hand, grasp the contour in which the EMF is induced when the magnetic flux changes, bend the thumb of this hand ninety degrees and direct it in the direction of the magnetic flux when it increases (or against the direction of the magnetic flux when it decreases), then the bent fingers will point in the direction opposite to the EMF.
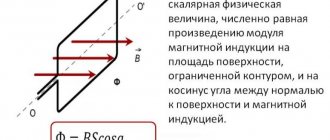
Lorentz force formula
The formula for calculating the Lorentz force is as follows:
Where q is the electric charge of the particle, V is its speed, and B is the magnitude of the magnetic induction of the magnetic field.
In this case, field B acts as a force perpendicular to the direction of the velocity vector V of the loads and the direction of vector B. This can be illustrated in the diagram:
Features of the Lorentz force
Since the Lorentz force is a force acting on a moving charge in a magnetic field, its magnitude depends on all three values: on the magnitude of the charge, on the speed and on the induction of the magnetic field:
$$F_L = qvB sin \alpha$$
However, the formula includes one more parameter - the angle $\alpha$, which characterizes the direction of the Lorentz force. This is the angle between the direction of movement of the charge carrier (its velocity vector) and the magnetic induction vector.
The fact is that, unlike many other forces, the direction of the Lorentz force does not coincide with either the direction of movement of the charge carrier or the direction towards the source of the magnetic field, and its occurrence depends on the mutual direction of the magnetic field and the speed of the charge. The Lorentz force is perpendicular to the plane formed by the vectors of magnetic induction and charge velocity.
Please note that if the direction of charge motion and the direction of the magnetic induction lines coincide, then the angle $\alpha$ is zero and there is no Lorentz force.
Rice. 2. Lorentz force.
Left hand rule
The left-hand rule allows physicists to determine the direction and return of the vector of magnetic (electrodynamic) energy. Imagine that our left hand is positioned in such a way that the magnetic field lines are directed perpendicular to the inner surface of the hand (so that they penetrate inside the hand), and all fingers except the thumb point in the direction of positive current flow, the deflected thumb indicates the direction of the electrodynamic force acting on a positive charge placed in this field.
This is how it will look schematically.
There is also a second way to determine the direction of the electromagnetic force. It consists of placing the thumb, index and middle fingers at right angles. In this case, the index finger will show the direction of the magnetic field lines, the middle finger will show the direction of current movement, and the thumb will show the direction of the electrodynamic force.
Left hand rule: what can be determined by using it
Do not confuse the rules of the left hand and the gimlet - they are intended for completely different purposes. With the help of your left hand you can determine two forces, or rather, their direction. This:
- Lorentz force;
- Ampere power.
Let's try to figure out how it works.
Application for Ampere power
Left hand rule for Ampere force: what is it?
Place your left hand along the conductor so that your fingers are directed in the direction the current flows. The thumb will point in the direction of the Ampere force vector, and the magnetic field vector will be directed in the direction of the hand, between the thumb and index finger. This will be the left-hand rule for ampere power, the formula of which looks like this:
Left hand rule for Lorentz force: differences from the previous one
We position the three fingers of the left hand (thumb, index and middle) so that they are at right angles to each other. The thumb, directed in this case to the side, will indicate the direction of the Lorentz force, the index finger (directed downwards) will indicate the direction of the magnetic field (from the north pole to the south), and the middle finger, located perpendicularly away from the thumb, will indicate the direction of the current in the conductor.
Application for Lorentz force
The formula for calculating the Lorentz force can be seen in the figure below.