Kirchhoff's first and second rules
The primary function of Kirchhoff's laws is the calculation of electrical circuits.
To describe the laws, the following concepts are introduced:
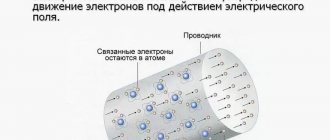
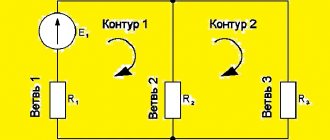
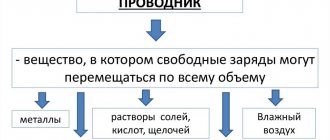
- A node is a point where several conductors of a galvanic circuit are connected.
- A branch is a section of a circuit diagram located between 2 nodes. An electric current with different charges but the same strength flows through it.
- A circuit is a closed path that crosses several branches and nodes of a branched galvanic circuit.
A branch and a node can be either parts of a single circuit or separate elements of several closed paths.
Statement of Kirchhoff's first rule for branched circuits: in electrical circuits with a series connection of the source and receiver of energy, the total number of currents flowing towards a node is equivalent to the total number of currents flowing away from the nodes. The energy flow towards the node is positive. The flow of particles directed away from the node is negative.
When adding 2 oppositely directed currents with the same value, the result will always be 0. The physical meaning of the first law is that the charge is not concentrated in the nodes of the galvanic circuit.
In other words, the current remains constant throughout the circuit.
To calculate direct current, the following formula is used : I 1 =I 2 +I 3. When using the first rule, instantaneous voltage values are additionally used to calculate alternating current. The formula is written in complex form, taking into account active and reactive components.
Kirchhoff's second law is a consequence of Maxwell's 3rd equation, which proves the absence of magnetic charges in nature. Definition of Kirchhoff's second rule: on the resistors of a closed circuit of a galvanic circuit, the sum of voltages is equivalent to the total number of EMF (electromotive force) calculated for the closed path. If the electrical circuit does not contain devices that generate EMF, then the sum of the voltages will be equal to 0.
The electromotive force is evenly distributed at all nodes of the electrical circuit. A separate case of the second rule is Ohm's law, which describes the relationship between emf and current in a conductor.
The second law applies to alternating current.
In this case, the total number of EMF amplitudes is equivalent to the total sum of voltage drops on all parts of the galvanic circuit.
When drawing up linear equations for the second law, it is necessary to correctly determine the direction of the stress drop.
An algorithm was developed to indicate the sign of this quantity:
- The direction to bypass the closed path is selected. The fall can move clockwise or counterclockwise.
- The direction of movement of energy flows flowing through the main parts of the electrical circuit is selected.
- If the direction of the circuit bypass coincides with the direction of the EMF, then a positive sign is given. If the directions do not coincide, then a negative symbol is placed.
When completing a complete detour of a closed path, the magnitude of the electromotive force takes on its original value.
Kirchhoff function. Pure black body
The energy flux emitted by a unit surface area of a radiating body in all directions (within a solid angle of 2π) is called energetic luminosity
body
R
, which is a function of body temperature and radiation frequency.
If the energy flux emanating from a unit surface of the body in the frequency range (ω, ω+dω
) is
dRω
, then at a small value
of dω
the flux
dRω
is proportional
to dω
:
(1.1)
Value rω
is called
the emissivity
of the body and also depends on the temperature of the body and the frequency of radiation. It is obvious that emissivity and energetic luminosity are interrelated functions:
(1.2)
Since radiation can be described not only by frequency ω
, but also the wavelength, which is inversely proportional to the frequency:
(1.3)
then the frequency spectrum interval dω
corresponds to a small section
dλ
on the wavelength scale:
(1.4)
According to the wavelength interval (λ, λ+dλ)
corresponds to energetic luminosity (1.5)
where rλ
–
emissivity
of the body in the wavelength range
(λ, λ+dλ)
. Then formula (1.2) needs to be rewritten as:
(1.2′)
Thus, it is possible to characterize a certain part of the spectrum by two interconnected intervals dω
and
dλ
. In this case, the emissivities are related by the relation:
(1.6)
Along with these parameters, absorption capacity
body in the frequency range
(ω, ω+dω)
, which is defined as the ratio of the flux of absorbed energy of electromagnetic radiation
dФ'ω
to the flux of incident radiation
dФω
.
(1.7)
Absorption capacity is a dimensionless quantity; its value cannot be greater than one.
Considering that the temperature (and therefore the energy) of bodies in thermodynamic equilibrium does not change, the body that emits more is forced to absorb more to maintain this equilibrium. Mathematically this can be expressed as follows:
(1.8)
where the indices are 1, 2, 3, etc. belong to different bodies.
This pattern was established by Gustav Kirchhoff: the ratio of emissivity and absorption abilities does not depend on the nature of the body, it is the same universal function of frequency (or wavelength) and temperature for all bodies
:
(1.9)
This function is called the Kirchhoff function
and is used in all major theoretical calculations concerning thermal radiation.
If in formula (1.9) rω
replace by
rλ
, that is, use the description of radiation using wavelengths, then instead of the “frequency” Kirchhoff function
f(ω,T)
we obtain the wavelength function
φ(λ,T)
, which is convenient to use in experimental studies.
(1.10)
It should be noted that it is necessary to understand the difference between the emission of radiation and its reflection. This process is observed along with emission and absorption, but does not affect the value of the Kirchhoff function (1.9). Radiation incident on a body is distributed into two parts - a flux of absorbed radiation and a flux of reflected radiation. The absorbed energy must be spent on emitting the same flux as was absorbed. Otherwise, the radiation could not satisfy the condition of thermodynamic equilibrium.
From Kirchhoff's law it follows that at a given temperature the maximum intensity will have rays of those frequencies (wavelengths) that the body absorbs most strongly at the same temperature.
A body characterized by the maximum possible absorption capacity aωT
= 1, is called
absolutely black
(ABL) - at any temperature it completely absorbs all the energy of incident electromagnetic waves, regardless of their frequency, polarization and direction of propagation.
From formula (1.9) it follows that the universal Kirchhoff function f(ω,T)
is the emissive ability of an absolutely black body.
Among real bodies there is no absolutely black body. However, there are bodies that are quite close in properties to absolute black in certain frequency ranges. In particular, for the visible part of the spectrum that is visible to humans, soot, platinum black, and black velvet are good approximations. These bodies have an absorptivity close to unity only in a limited frequency range; in the far infrared region aωТ
noticeably less than one.
Fig.1.2. Blackbody model
To study the radiation spectrum of a black body at different temperatures, an almost closed cavity equipped with a small hole is used. Experience shows that if the hole size is less than 1/10 of the cavity diameter, incident radiation of all frequencies is completely absorbed. We see a similar situation every day: open windows of houses from the street side appear black, although inside the rooms it is quite light due to the reflection of light from the walls. Through a window or through a hole (in the model under consideration - see Fig. 1.2), radiation enters the cavity and, before leaving it, undergoes multiple reflections. Each of these reflections is accompanied by the absorption of part of the energy, as a result of which almost all radiation of any frequency is absorbed by the cavity. According to Kirchhoff's law, the emissivity of such a device is very close to f(ω,T)
at a temperature equal to the temperature of the cavity walls. That is, if the temperature of the walls of the cavity is constant, then the radiation emerging from the hole will be quite close to the radiation of a black body at the specified temperature.
If this radiation is decomposed into its components, then we get a curve of the dependence of the radiation intensity of an absolutely black body on the wavelength, that is, the spectrum of its radiation.
Fig.1.3. Blackbody radiation spectrum
Black body emissivity spectrum curve shape
(Fig. 1.3) and the position of its maximum
λmax
depend on body temperature.
The area under the curve is equal to the energy luminosity RT
of the body at a given temperature (see formula 1.2). It was found that the spectral radiation curve for a body with a lower temperature fits under the curve for a body with a higher temperature, that is, as the temperature decreases, the energy flow emitted per unit surface of the body decreases.
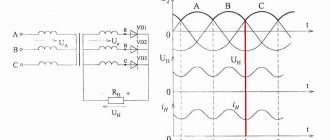
Writing equations
When calculating an electrical circuit using Kirchhoff's rules, current equations are drawn up. The number of equations is directly dependent on the number of nodes in the chain. They are also used to describe physical phenomena in the industrial sector: in the manufacture of liquid pipelines and electric pumps.
When composing the equation, you must be guided by the following algorithm:
- Select the direction of flow of charged particles on the branches indicated on the electrical diagram.
- Select voltages with the same direction of bypassing the closed circuit.
- Select contours with different branches and nodes to apply the second rule.
Many physicists have difficulty writing linear equations for a galvanic circuit located in complex nonplanar graphs—mathematical objects with minors obtained by contracting 1 edge. In this case, to calculate the electrical circuit, it is necessary to create a system of equations that combines expressions for both the first and second Kirchhoff laws.
In them, the calculation of closed paths is carried out using graph theory, a branch of discrete mathematics.
To check the correctness of linear composition, a potential diagram is used, which is a graphical image. It is built for the galvanic circuit circuit. If the beginning and end points of the diagram have identical potentials, independent of the direction of current movement, then the equation is correct.
Part 4
OPTICS. SPECIAL THEORY OF RELATIVITY
Section 13 CORPUSCULAR PROPERTIES OF LIGHT
13.1. Thermal radiation of bodies. Kirchhoff's law
The most common is the radiation of bodies, associated with the thermal movement of atoms and molecules. This type of radiation is called thermal (or temperature). Thermal radiation is characteristic of all bodies without exception at temperatures higher than absolute zero, but at low temperatures almost only long (infrared) electromagnetic waves are emitted.
The average radiation power over a time that significantly exceeds the period of light oscillations is called radiation flux (radiant flux); in SI it is expressed in watts.
The radiation flux per unit surface that emits is called energetic luminosity (integral radiant flux density). Its SI unit of measurement is 1 W/m2.
Let us consider the radiation of condensed systems consisting of a large number of strongly interacting particles. This makes it possible to use methods of thermodynamics and statistical physics to study the phenomenon of radiation. The application of the laws of thermodynamics and statistical physics is justified when the system under study is in thermodynamic equilibrium. Let us consider the equilibrium radiation of bodies. In this case, in the radiating medium, all thermodynamic parameters (including temperature) are steel. According to the macroscopic method of considering phenomena, the power of radiation will belong to one individual atom or molecule, and to the radiating body as a whole or to any part of its radiating surface.
For the spectral characteristics of thermal radiation, the concept of the emissivity of a body Eλ, T is introduced, which is numerically equal to the energy emitted per unit time by a unit surface of this body in a unit wavelength range of the spectrum near a certain wavelength λ. The quantity Eλ,T) is often called the spectral density of the body's energy luminosity.
The absorption capacity (spectral absorption coefficient) Aλ,T is understood as a fraction that shows what part of the radiation energy of a certain wavelength incident on a unit surface of a body is absorbed by the body per unit time. Similarly, the vibrational (spectral reflection coefficient) and transmittance (spectral transmittance coefficient) Dλ,T abilities of the body are determined.
Based on the law of conservation of energy, we can write that
The quantities Aλ,T, Rλ,T, Dλ,T depend on the length of the incident waves, the temperature of the body, its chemical composition and the state of the surface.
A body that does not transmit (Dλ,T = 0) or reflect (Rλ,T = 0) radiation of all wavelengths, but completely absorbs them at any temperature, is called absolutely black. The absorption coefficient (absorption capacity) of an absolutely black body is equal to unity (Aλ,T = 1).
A body that completely reflects the energy of radiation incident on it is called an ideal mirror. For it, Aλ,T = 0, Dλ,T = 0, and Rλ,T = 1. An ideal mirror, like an absolutely black body, does not exist in nature. As a rule, the absorption capacity A(λ,T is not the same for different parts of the spectrum. If the absorption capacity of a body is the same for rays of all colors (all wavelengths) and less than one, then such a body is called absolutely gray. It has been established that the emissive and absorbing abilities of bodies are proportional. Thus, soot or platinum black have high absorption coefficients and high radiation density. On the contrary, polished silver is characterized by a low absorption coefficient and low radiation density.
The results of experimental studies and thermodynamic reasoning prompted G. Kirchhoff in 1859 to discover the law of thermal radiation, named after him. It is formulated as follows: for all bodies, regardless of their nature, the ratio of emissivity Eλ,T to absorption capacity λ,T at a given temperature and for the same wavelengths is a universal function of wavelength and temperature. So,
Here the indices 1,2,…, n mean the first, second, etc. body. To clarify the physical meaning of the universal function f(λ,T), let us assume that one of these bodies is absolutely black. Let us denote its emissivity by rλ,T. Then, taking into account that for an absolutely black body A(λ,T = 1), we can rewrite Kirchhoff’s law in the form
So, the universal Kirchhoff function f(λ,T) is the emissivity of a black body for a certain wavelength and at the same temperature. From relation (13.3) it follows that Eλ,T = Aλ,Trλ,T. Since for all bodies that are not completely black, Aλ,T < 1, then E(λ,T < rλ,T. The inequality indicates that for a given temperature the thermal radiation of any body in any region of the spectrum is always less than the thermal radiation absolutely black body in this spectral region. From relation (13.3) one more conclusion can be drawn: if a body does not absorb waves of a certain length, then it does not emit them. Indeed, Eλ,T = Aλ,Trλ,T therefore at Aλ,T = 0 i Еλ,T = 0.
Problem solving
In physics, there are several types of problems using Kirchhoff's laws, where you need to find either the current strength or the emf of an energy source in a galvanic circuit.
Examples of analyzed problems based on Kirchhoff’s rules:
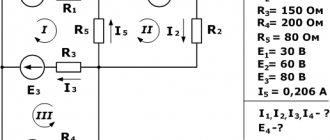
- An electrical diagram is given that shows EMF sources and 3 resistors connected in parallel. It is necessary to find the magnitude of the current in the circuit if the values of resistance and electromotive force are indicated. Initially, you need to determine the number of nodes and create an equation based on the first law. In this case, the incoming and outgoing energy flows are considered equal in magnitude, but different in direction. Then equations are constructed using the second law, taking into account the value of emf and resistance. After composing the equation for all circuits, a system is formed. The final step is to substitute known quantities into the equation.
- A galvanic diagram is given, where 5 resistors and galvanometers are displayed. Resistances of 4 of them are known. It is required to find the current strength for 1 - 4 resistors and the EMF for 4 galvanometers, if the current value for source 5 is known. First, an equation for the first law is drawn up. You get 2 equalities. Then equations are compiled according to the second rule. This results in 3 equalities for the same number of contours. The result is a system of 5 equations. The final stage is solving the system with the substitution of known values.
All problems using Kirchhoff's laws are solved by composing equations based on 2 laws. The result is checked using a power balance.
When performing calculations, it is recommended to use online calculators for working with large numbers.
Kirchhoff's laws in chemistry
Kirchhoff spent a long time studying chemistry, investigating thermal phenomena. The scientist developed a law for determining the temperature coefficient when heat is released during a chemical reaction. This is true for both organic and inorganic substances. To describe the law, the concepts of isobaric and isochoric capacitance are introduced, denoted by the symbols CP and CV. The law states that the temperature coefficient of a chemical reaction is equivalent to the amplitude of the change in heat capacity.
In differential form, the law determines the dependence of the change in the thermal effect on an increase or decrease in temperature. The magnitude of the thermal effect is calculated using Hess's law, which takes into account the type of reaction. Heat release will increase during endothermic reactions and decrease during exothermic reactions.
When calculating temperature, it is important to take into account the state of aggregation , true or average heat capacity, qualitative composition and type of substances mixed in the solution. These characteristics are tabular values and are indicated in chemical reference books. Based on the data obtained, an equation is drawn up that establishes the analytical dependence of the thermal effect on the temperature value.