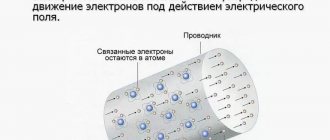
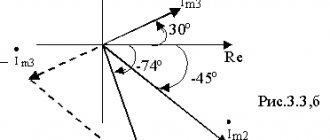
Первое и второе правила Кирхгофа
Первоначальной функцией законов Кирхгофа является расчет электрических цепей.
Для описания законов вводятся следующие понятия:
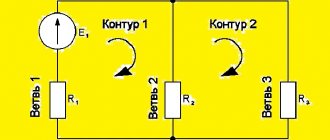
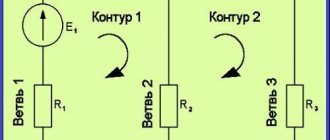
- Узел — точка, являющаяся местом соединения нескольких проводников гальванической цепи.
- Ветвь — участок схемы цепи, расположенный между 2 узлами. По ней протекает электрический ток с разными зарядами, но одинаковой силой.
- Контур — закрытый путь, пересекающий несколько ветвей и узлов разветвленной гальванической цепи.
Ветвь и узел способны быть как частями единого контура, так и отдельными элементами нескольких замкнутых путей.
Формулировка первого правила Кирхгофа для разветвленных цепей: в электрических схемах с последовательным соединением источника и приемника энергии суммарное количество токов, текущих по направлению к узлу, эквивалентно общему числу токов, текущих по направлению от узлов. Поток энергии, направленный к узлу, является положительным. Поток частиц, направленных от узла, является отрицательным.
При сложении 2 противоположно направленных токов с одинаковой величиной будет всегда получаться 0. Физический смысл первого закона заключается в том, что заряд не концентрируется в узлах гальванической схемы.
Иными словами, ток остается постоянным на всех участках цепи.
Для расчета силы постоянного тока используется следующая формула: I 1 =I 2 +I 3. При использовании первого правила для расчета переменного тока дополнительно применяются величины мгновенного напряжения. Формула записывается в комплексной форме с учетом активных и реактивных составляющих.
Второй закон Кирхгофа является следствием 3 уравнения Максвелла, доказывающего отсутствие магнитных зарядов в природе. Определение второго правила Кирхгофа: на резисторах закрытого контура гальванической цепи сумма напряжений эквивалентна общему числу ЭДС (электродвижущей силы), рассчитанной для замкнутого пути. Если в составе электрической схемы не присутствуют приборы, вырабатывающие ЭДС, то сумма напряжений будет равняться 0.
Электродвижущая сила равномерно распределяется на всех узлах электрической цепи. Отдельным случаем второго правила является закон Ома, описывающий соотношение ЭДС и силы тока в проводнике.
Второй закон применяется к переменному току.
В этом случае суммарное количество амплитуд ЭДС эквивалентно общей сумме падений напряжений на всех частях гальванической цепи.
При составлении линейных уравнений для второго закона необходимо правильно определить направление падения напряжений.
Для указания знака этой величины был разработан алгоритм:
- Отбирается направление обхода замкнутого пути. Падение способно двигаться по или против часовой стрелки.
- Выбирается направление движения потоков энергии, текущих через основные части электрической цепи.
- Если направление обхода контура совпадает с направлением ЭДС, то ставится положительный знак. Если направления не совпадают, то ставится отрицательный символ.
При совершении полного обхода замкнутого пути величина электродвижущей силы принимает первоначальное значение.
Функция Кирхгофа. Абсолютно черное тело
Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π), называют энергетической светимостью
тела
R
, которая является функцией температуры тела и частоты излучения. Если поток энергии, исходящий с единичной поверхности тела в интервале частот (ω,
ω+dω
) составляет
dRω
, то при малом значении
dω
поток
dRω
пропорционален
dω
:
(1.1)
Величина rω
называется
испускательной способностью
тела и также является зависящей от температуры тела и частоты излучения. Очевидно, что испускательная способность и энергетическая светимость являются взаимосвязанными функциями:
(1.2)
Поскольку излучение может быть описано не только частотой ω
, но и длиной волны, которая обратно пропорциональна частоте:
(1.3)
то интервалу частотного спектра dω
соответствует малый участок
dλ
по шкале длин волн:
(1.4)
Соответственно интервалу длин волн (λ, λ+dλ)
отвечает энергетическая светимость (1.5)
где rλ
–
испускательная способность
тела в диапазоне длин волн
(λ, λ+dλ)
. Тогда формулу (1.2) нужно переписать в виде:
(1.2′)
Таким образом, можно охарактеризовать определенный участок спектра двумя взаимосвязанными интервалами dω
и
dλ
. В этом случае испускательные способности связаны соотношением:
(1.6)
Наряду с этими параметрами рассматривают поглощательную способность
тела в интервале частот
(ω, ω+dω)
, которая определяется как отношение потока поглощенной энергии электромагнитного излучения
dФ’ω
к потоку падающего излучения
dФω
.
(1.7)
Поглощательная способность является безразмерной величиной, ее значение не может быть больше единицы.
Учитывая, что температура (следовательно и энергия) тел в термодинамическом равновесии не меняется, то тело, которое больше испускает, вынуждено для поддержания этого равновесия больше поглощать. Математически это можно выразить следующим образом:
(1.8)
где индексы 1, 2, 3 и т.д. относятся к разным телам.
Эту закономерность установил Густав Кирхгоф: отношение испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же универсальной функцией частоты (или длины волны) и температуры
:
(1.9)
Эта функция называется функцией Кирхгофа
и используется во всех основных теоретических расчетах, касающихся теплового излучения.
Если в формуле (1.9) rω
заменить на
rλ
, то есть воспользоваться описанием излучения с помощью длин волн, то вместо «частотной» функции Кирхгофа
f(ω,Т)
получим функцию длин волн
φ(λ,Т)
, которой удобно пользоваться при экспериментальных исследованиях.
(1.10)
Следует заметить, что необходимо понимать различие между испусканием излучения и его отражением. Этот процесс наблюдается наряду с испусканием и поглощением, но на значении функции Кирхгофа (1.9) не сказывается. Падающее на тело излучение распределяется на две части – поток поглощенного и поток отраженного излучений. Поглощенная энергия должна израсходоваться на испускание такого же потока, какой был поглощен. В противном случае излучение не могло бы удовлетворять условию термодинамического равновесия.
Из закона Кирхгофа следует, что при данной температуре максимальной интенсивностью будут обладать лучи тех частот (длин волн), которые тело при той же температуре сильнее всего поглощает.
Тело, которое характеризуется максимально возможной поглощательной способностью аωТ
= 1, называют
абсолютно черным
(АЧТ) – оно при любой температуре полностью поглощает всю энергию падающих электромагнитных волн независимо от их частоты, поляризации и направления распространения. Из формулы (1.9) следует, что универсальная функция Кирхгофа
f(ω,Т)
– это испускательная способность абсолютно черного тела.
Среди реальных тел нет абсолютно черного тела. Однако существуют тела, которые довольно близки по свойствам к абсолютно черному в определенных диапазонах частот. В частности, для наглядной человеку видимой части спектра хорошим приближением являются сажа, платиновая чернь, черный бархат. Эти тела имеют поглощательную способность близкую к единице лишь в ограниченном диапазоне частот, в далекой инфракрасной же области аωТ
заметно меньше единицы.
Рис.1.2. Модель АЧТ
Для изучения спектра излучения АЧТ при различных температурах используют почти замкнутую полость, снабженную малым отверстием. Опыт показывает, что если размер отверстия меньшего 1/10 диаметра полости, падающее излучение всех частот полностью поглощается. Аналогичную ситуацию мы наблюдаем каждый день: открытые окна домов со стороны улицы кажутся черными, хотя внутри комнат достаточно светло из-за отражения света от стен. Через окно или через отверстие (в рассматриваемой модели – см. рис. 1.2) излучение попадает внутрь полости и, прежде чем выйти из него, претерпевает многократные отражения. Каждое из таких отражений сопровождается поглощением части энергии, в результате чего практически все излучение любой частоты поглощается полостью. Согласно закону Кирхгофа испускательная способность такого устройства очень близка к f(ω,Т)
при температуре равной температуре стенок полости. То есть, если температура стенок полости является постоянной, то излучение, выходящее из отверстия, будет достаточно близко к излучению абсолютно черного тела при указанной температуре.
Если это излучение разложить на составляющие, то получится кривая зависимости интенсивности излучения абсолютно черного тела от длины волны, то есть спектр его излучения.
Рис.1.3. Спектр излучения АЧТ
Форма кривой спектра испускательной способности черного тела
(рис. 1.3) и положение ее максимума
λmax
зависят от температуры тела. Площадь под кривой равна энергетической светимости
RT
тела при данной температуре (см. формулу 1.2). Было получено, что спектральная кривая излучения для тела с меньшей температурой укладывается под кривой для тела с большей температурой, то есть при снижении температуры уменьшается поток энергии, испускаемый единицей поверхности тела.
Составление уравнений
При расчете электрической цепи при помощи правил Кирхгофа составляются уравнения токов. Количество уравнений находится в прямой зависимости от числа узлов в цепи. Они используются для описания физических явлений и в промышленном секторе: при изготовлении жидкостных трубопроводов и электрических насосов.
При составлении уравнения нужно руководствоваться следующим алгоритмом:
- Выбрать направление потоков заряженных частиц на ветвях, обозначенных на электрической схеме.
- Отобрать напряжения с одинаковым направлением обхода закрытого контура.
- Выбрать контуры с разными ветвями и узлами для применения второго правила.
Многие физики сталкиваются с трудностями при составлении линейных уравнений для гальванической цепи, расположенной в сложных непланарных графах — математических объектах с минорами, полученными при помощи стягивания 1 ребра. В этом случае для расчета электрической цепи необходимо составить систему уравнений, где совмещены выражения как для первого, так и для второго законов Кирхгофа.
В них подсчет замкнутых путей осуществляется посредством теории графов — раздела дискретной математики.
Для проверки правильности составления линейных используется потенциальная диаграмма, представляющая собой графическое изображение. Она строится для контура гальванической цепи. Если точки начала и конца диаграммы обладают идентичными потенциалами, независимыми от направления движения тока, то уравнение составлено верно.
Часть 4
ОПТИКА. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Раздел 13 КОРПУСКУЛЯРНЫЕ СВОЙСТВА СВЕТА
13.1. Тепловое излучение тел. Закон Кирхгофа
Самым распространенным является излучение тел, связано с тепловым движением атомов и молекул. Этот вид излучения называют тепловым (или температурным). Тепловое излучение свойственно всем без исключения телам при температурах выше чем абсолютный ноль, но при низких температур излучаются практически лишь длинные (инфракрасные) электромагнитные волны.
Среднюю мощность излучения за время, что значительно превышает период световых колебаний, называют потоком излучения (лучистым потоком); в СИ он выражается в ваттах.
Поток излучения, отнесенный к единицы поверхности, которая излучает, называют энергетической светимости (интегральная плотность лучистого потока). Единицей измерения ее в СИ является 1 Вт/м2.
Рассмотрим излучение конденсированных систем, состоящих из большого числа сильно взаимодействующих частиц. Это дает возможность для исследования явления излучения использовать методы термодинамики и статистической физики. Применение законов термодинамики и статистической физики оправдано тогда, когда исследуемая система находится в термодинамическом равновесии. Рассмотрим равновесное излучение тел. В этом случае в излучающем среде все термодинамические параметры (в том числе и температура) стали. По макроскопическим методом рассмотрения явлений мощность излучение будет принадлежать до одного отдельного атома или молекулы, а к излучающего тела как целого или любой части его излучательной поверхности.
Для спектральной характеристики теплового излучения вводят понятие о излучательную способность тела Еλ,T которая численно равна энергии, излучается за единицу времени единицей поверхности этого тела в единичном интервале длин волн спектра вблизи некоторой длины волны λ. Величину Еλ,T ) часто называют спектральной плотностью энергетической светимости тела.
Под поглощательной способностью (спектральный коэффициент поглощения) Aλ,T понимают дробь, показывает, какая часть падающей на единицу поверхности тела энергии излучения определенной длины волны поглощается телом за единицу времени. Аналогично определяют відбивальну (спектральный коэффициент отражения) и пропускную (спектральный коэффициент пропускания) Dλ,T способности тела.
Исходя из закона сохранения энергии, можно записать, что
Величины Аλ,T, Rλ,T, Dλ,T зависят от длины падающих волн, температуры тела, его химического состава и состояния поверхности.
Тело, которое не пропускает (Dλ,T = 0) и не отражает (Rλ,T = 0) излучения всех длин волн, а полностью поглощает их при любой температуре, называют абсолютно черным. Коэффициент поглощения (поглощательная способность) абсолютно черного тела равен единице (Aλ,T = 1).
Тело, которое полностью отражает энергию излучения, падающего на него, называют идеальным зеркалом. Для него Аλ,T = 0, Dλ,T = 0, а Rλ,T = 1. Идеального зеркала, как и абсолютно черного тела, в природе не существует. Как правило, поглощательная способность А(λ,T неодинакова для различных участков спектра. Если поглощательная способность тела одинакова для лучей всех цветов (всех длин волн) и меньше за единицу, то такое тело называют абсолютно серым. Установлено, что излучательные и поглощающие способности тел пропорциональны. Так, сажа или платиновая чернь имеют большие коэффициенты поглощения и большую плотность излучения. Наоборот, полированное серебро характеризуется малым коэффициентом поглощения и малой плотностью излучения.
Результаты экспериментальных исследований и термодинамические рассуждения побудили Г. Кирхгофа 1859 г. к открытие закона теплового излучения, названного его именем. Он формулируются так: для всех тел, независимо от их природы, отношение излучательной способности Еλ,T к поглотительной способностиλ,T при заданной температуре и для одинаковых длин волн является универсальной функцией длины волны и температуры. Итак,
Здесь индексы 1,2,…, n означают первое, второе и т. д. тело. Для выяснения физического смысла универсальной функции f(λ,T) предположим, что одно из этих тел абсолютно черное. Обозначим его излучательную способность через rλ,T. Тогда, учитывая, что для абсолютно черного тела А(λ,T =1, можно переписать закон Кирхгофа в виде
Итак, универсальная функция Кирхгофа f(λ,T) является излучательной способностью абсолютно черного тела для определенной длины волны и при той же температуре. С соотношение (13.3) следует, что Еλ,T = Аλ,Trλ,T. Поскольку для всех тел, не является абсолютно черными, Аλ,T < 1, то Е(λ,T < rλ,T. Неравенство свидетельствует о том, что за заданной температуры тепловое излучение любого тела в любой области спектра всегда меньше, чем тепловое излучение абсолютно черного тела в этой спектральной области. Из соотношения (13.3) можно достать еще один вывод: если тело не поглощает волн определенной длины, то оно и не излучает их. Действительно, Еλ,T = Аλ,Trλ,T поэтому при Аλ,T = 0 i Еλ,T = 0.
Решение задач
В физике присутствует несколько видов задач на законы Кирхгофа, где требуется найти либо силу тока, либо ЭДС источника энергии в гальванической цепи.
Примеры разобранных задач на правила Кирхгофа:
- Дана электрическая схема, на которой изображены источники ЭДС и 3 резистора, соединенных параллельно. Необходимо найти величину силы тока в цепи, если указаны значения сопротивления и электродвижущей силы. Изначально нужно определить количество узлов и составить уравнение на основе первого закона. В этом случае входящие и выходящие потоки энергии считаются равными по модулю, но разными по направлению. Затем составляются уравнения с использованием второго закона, учитывая значение ЭДС и сопротивления. После составления уравнения для всех контуров образуется система. Финальным шагом является подстановка известных величин в уравнение.
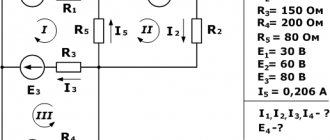
- Дана гальваническая схема, где отображены 5 резисторов и гальванометров. Известны сопротивления 4 из них. Требуется найти силу тока для 1 — 4 резисторов и ЭДС для 4 гальванометра, если известна величина тока для 5 источника. В начале составляется уравнение для первого закона. Получится 2 равенства. После составляются уравнения по второму правилу. Получается 3 равенства для аналогичного количества контуров. В результате получится система из 5 уравнений. Финальным этапом является решение системы с подстановкой известных значений.
Все задачи на законы Кирхгофа решаются методом составления уравнений, основываясь на 2 законах. Проверка результата осуществляется при помощи баланса мощностей.
Во время проведения вычислений рекомендуется использовать онлайн-калькуляторы для работы с большими числами.
Законы Кирхгофа в химии
Кирхгоф в течение долгого времени занимался изучением химии, исследуя тепловые явления. Ученый разработал закон для определения коэффициента температуры при выделении теплоты во время осуществления химической реакции. Оно справедливо как для органических, так и для неорганических веществ. Для описания закона вводятся понятия изобарной и изохорной емкости, обозначаемые символами CP и CV. Закон гласит, что температурный коэффициент химической реакции эквивалентен амплитуде изменения теплоемкости.
В дифференциальной форме закон определяет зависимость изменения теплового эффекта от повышения или понижения температуры. Величина теплового эффекта высчитывается при помощи закона Гесса, где учитывается тип реакции. Тепловыделение будет увеличиваться при эндотермических реакциях, уменьшаться — при экзотермических реакциях.
Во время расчета температуры важно учитывать агрегатное состояние, истинную или среднюю теплоемкость, качественный состав и вид веществ, смешанных в растворе. Эти характеристики являются табличными величинами и указаны в химических справочниках. На основе полученных данных составляется уравнение, устанавливающее аналитическую зависимость теплового эффекта от значения температуры.