Алгоритм решения задач на законы Кирхгофа
Задачи на применение закона Кирхгофа решаются в школе не часто, и не во всех классах. Работая в школе, я давала законы Кирхгофа только тем ребятам, кто готовился к олимпиадам по физике, и учащимся, которые готовились в ВУЗы.
Задачи на использование законов Кирхгофа есть даже не всех сборниках задач, рекомендованных для использования в средней школе.
Ниже приведён алгоритм решения задач по данной теме. Алгоритм не сложен. Использование данного алгоритма поможет Вам в решении задач по этой теме.
Итак, начнем. Сначала необходимо выполнить некоторые подготовительные операции.
- перерисовать схему
- указать направление ЭДС источников тока
- указать предполагаемое направление токов, текущих в каждом резисторе (если итоговый ответ будет отрицательным, то направление тока было изначально выбрано не верно)
- выбрать направление обхода для всех линейно независимых контуров
После проведения предварительных операций, приступаем собственно к решению самой задачи.
- Записываем первый закон Кирхгофа: сумма токов, втекающих и вытекающих в данный узел, равна нулю.
Важно! Если ток втекает в узел, то он берётся со знаком «плюс», если вытекает, то со знаком «минус». Число уравнений второго закона Кирхгофа равно n-1, где n — число узлов в данной схеме. (Узел — точка, в которой соединяются три проводника и более).
- Записываем второй закон Кирхгофа для всех линейно независимых контуров: Сумма ЭДС в контуре равно сумме падений напряжений в каждом из этих контуров.
Важно! Если направление ЭДС совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «плюс». Если направление ЭДС не совпадает с направлением обхода контура, то значение ЭДС берётся со знаком «минус». Если направление тока совпадает с направлением обхода контура, то падение напряжения на данном участке берётся со знаком «плюс». Если направление тока через какой-либо резистор не совпадает с направлением обхода в данном контуре, то падение напряжения берётся со знаком «минус».
Решаем систему получившихся уравнений, относительно неизвестных величин.
Чаще всего в задачах этого типа, основную сложность представляет именно решение системы получившихся уравнений.
Ниже показан пример решения задачи с использованием законов Кирхгофа. Обратите внимание ещё раз на основные этапы решения. Они полностью соответствуют алгоритму, описанному выше.
Вот условие этой задачи.
Электрическая цепь состоит из двух гальванических элементов, трех резисторов и амперметра. В этой цепи R1 = 100 Ом, R2 = 50 Ом, R3 = 20 Ом, ЭДС элемента ?1 = 2 В. Амперметр регистрирует ток I3 = 50 мА, идущий в направлении, указанном стрелкой. Определить ЭДС ?2 второго элемента. Сопротивлением амперметра и внутренним сопротивлением источников пренебречь.
Удачи в освоении этой довольно сложной темы!
Возникающие вопросы можете оставлять в комментариях.
Источник
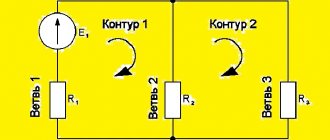
Задача 2
Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.
Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2
Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.
На основании этих уравнений составляем систему с 5-ью неизвестными
Решив эту систему любым удобным способом, найдем неизвестные величины
Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Прочитав статейки про первый и второй законы Кирхгофа, уважаемый читатель может сказать: «Хорошо, MyElectronix, ты рассказал мне, конечно, интересные штуки, но что мне дальше с ними делать? Пока по твоим словам я заключил, что если я соберу ручками схему, то я смогу в каждом ее узле и в каждом контуре намерить вот такие вот зависимости. Это здорово, но я хотел бы рассчитывать схемы, а не просто наблюдать зависимости!»
Господа, все эти замечания абсолютно верные и в ответ на них можно лишь рассказать о расчете электрических схем с помощью законов Кирхгофа. Без лишних слов перейдем сразу к делу!
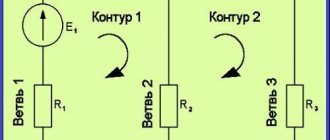
Начнем с самого простейшего случая. Он изображен на рисунке 1. Допустим, ЭДС источника питания равна Е1=5 В, а сопротивления R1=100 Ом, R2=510 Ом, R3=10 кОм. Требуется рассчитать напряжения на резисторах и ток через каждый резистор.
Господа, замечу сразу, эту задачу можно решить гораздо более простым способом, чем с применением законов Кирхгофа. Однако сейчас наша задача не искать оптимальные способы решения, а на наглядном примере рассмотреть методику применения законов Кирхгофа при расчете схем.
Рисунок 1 – Простая схема
В этой схеме мы можем видеть три контура. Если возник вопрос – а почему три, то рекомендую посмотреть статью про второй закон Кирхгофа . В той статье имеется практически такая же схема с наглядным пояснением методики расчета числа контуров.
Господа, хочу отметить один тонкий момент. Хоть контура и три, независимых из них только два. Третий контур включает в себя все остальные и не может считаться независимым. И вообще всегда при всех расчетах мы должны использовать только независимые контура. Не поддавайтесь искушению записать еще одно уравнение за счет этого общего контура, ничего хорошего не выйдет .
Итак, будем использовать два независимых контура. Для этого зададимся в каждом контуре направлением обхода контура. Как мы уже говорили, это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода каждого контура нарисуем синей стрелкой.
Далее зададимся направлением токов в ветвях: просто проставим его наугад. Не важно, угадаем мы сейчас направление или нет. Если угадали, то в конце расчета мы получим ток со знаком плюс, а если ошиблись – со знаком минус. Итак, обозначим токи в ветвях черными стрелочками с подписями I1, I2, I3.
Расчет электрической цепи по закону Кирхгофа
Содержание:
Законы Кирхгофа
Уравнения, описывающие поведение электрической цепи, составляют на основе законов Кирхгофа. Они определяют связь между токами и напряжениями элементов, образующих цепь. Уравнения, составленные согласно этим законам, называют уравнениями Кирхгофа.
Первый закон Кирхгофа определяет баланс токов в узлах электрической цепи.
Он формулируется следующим образом:
Алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:
В уравнении (3.1) токи, направленные от узла, записывают с положительным знаком. Токи, направленные к узлу, записывают со знаком минус.
Система уравнений по первому закону Кирхгофа, записанная для всех узлов цепи, линейно зависима. В этом легко убедиться, сложив все уравнения. Поскольку ток каждой ветви входит в два уравнения с разными знаками, сумма тождественно равна нулю. Поэтому число независимых уравнений по первому закону Кирхгофа равно
, где — число узлов цепи.
По этой ссылке вы найдёте полный курс лекций по теоретическим основам электротехники (ТОЭ):
Второй закон Кирхгофа устанавливает баланс напряжений в контуре цепи:
Алгебраическая сумма напряжений ветвей в контуре равна нулю:
Если напряжение ветви совпадает с направлением обхода контура, то напряжению приписывают знак плюс, если же нет — знак минус. Перенесем напряжения источников напряжения, равные ЭДС этих источников, в правую часть. Уравнение (3.2) примет вид
В соответствии с последним равенством алгебраическая сумма напряжений ветвей в контуре электрической цепи равна алгебраической сумме ЭДС источников.
Число независимых уравнений, записанных по второму закону Кирхгофа, равно числу независимых контуров. Число таких контуров определяется формулой
, где — число ветвей.
Возможно вам будут полезны данные страницы:
Порядок составления уравнений но законам Кирхгофа
1. Необходимо сначала выбрать положительные направления токов и напряжений ветвей. Положительное направление тока показывают стрелкой на выводе элемента. Положительное направление напряжения показывают стрелкой, расположенной рядом с элементом. Полярности напряжений резисторов выбирают согласованными с направлениями токов. Направления токов источников напряжения выбирают совпадающими с направлениями ЭДС.
2. Записываем уравнения по первому закону Кирхгофа для
узлов.
3. Выбираем направления обхода контуров и записываем уравнения по законам Кирхгофа. Сопротивление проводника, соединяющего элементы, очень мало по сравнению с сопротивлением резистора и игнорируется. Ячейки внутренней цепи удобно выбирать в качестве независимых цепей. Можно воспользоваться и другим способом: выбрать по порядку контуры, так, чтобы каждый следующий контур содержал, по меньшей мере, одну ветвь, не входящую в предыдущие контуры.
4. Решаем полученную систему уравнений и определяем токи и напряжения цепи.
5. После определения токов и напряжений необходимо выполнить проверку. Для этого вычисленные значения переменных подставляют в одно из уравнений, составленных по законам Кирхгофа.
При составлении уравнений в качестве неизвестных рассматривают либо токи, либо напряжения резистивных элементов.
В первом случае уравнения цепи составляют относительно неизвестных токов резистивных элементов и напряжений на источниках тока. Напряжения на резистивных элементах, входящие в уравнения по второму закону Кирхгофа, выражают через токи по закону Ома. Такой способ составления уравнений называют токов ветвей.
Число совместно решаемых уравнений в методе токов ветвей можно сократить, если контуры выбирать так, чтобы они не включали источники тока. В этом случае неизвестными будут только токи резистивных элементов, и по второму закону Кирхгофа достаточно составить
уравнений, где — количество источников тока.
Постоянный ток
Прочитав статейки про первый и второй законы Кирхгофа, уважаемый читатель может сказать: «Хорошо, MyElectronix, ты рассказал мне, конечно, интересные штуки, но что мне дальше с ними делать? Пока по твоим словам я заключил, что если я соберу ручками схему, то я смогу в каждом ее узле и в каждом контуре намерить вот такие вот зависимости. Это здорово, но я хотел бы рассчитывать схемы, а не просто наблюдать зависимости!»
Господа, все эти замечания абсолютно верные и в ответ на них можно лишь рассказать о расчете электрических схем с помощью законов Кирхгофа. Без лишних слов перейдем сразу к делу!
Начнем с самого простейшего случая. Он изображен на рисунке 1. Допустим, ЭДС источника питания равна Е1=5 В, а сопротивления R1=100 Ом, R2=510 Ом, R3=10 кОм. Требуется рассчитать напряжения на резисторах и ток через каждый резистор.
Господа, замечу сразу, эту задачу можно решить гораздо более простым способом, чем с применением законов Кирхгофа. Однако сейчас наша задача не искать оптимальные способы решения, а на наглядном примере рассмотреть методику применения законов Кирхгофа при расчете схем.
Рисунок 1 – Простая схема
В этой схеме мы можем видеть три контура. Если возник вопрос – а почему три, то рекомендую посмотреть статью про второй закон Кирхгофа . В той статье имеется практически такая же схема с наглядным пояснением методики расчета числа контуров.
Господа, хочу отметить один тонкий момент. Хоть контура и три, независимых из них только два. Третий контур включает в себя все остальные и не может считаться независимым. И вообще всегда при всех расчетах мы должны использовать только независимые контура. Не поддавайтесь искушению записать еще одно уравнение за счет этого общего контура, ничего хорошего не выйдет .
Итак, будем использовать два независимых контура. Для этого зададимся в каждом контуре направлением обхода контура. Как мы уже говорили, это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода каждого контура нарисуем синей стрелкой.
Далее зададимся направлением токов в ветвях: просто проставим его наугад. Не важно, угадаем мы сейчас направление или нет. Если угадали, то в конце расчета мы получим ток со знаком плюс, а если ошиблись – со знаком минус. Итак, обозначим токи в ветвях черными стрелочками с подписями I1, I2, I3.
Мы видим, что в контуре №1 направление токов I1 и I3, а также направление источника питания совпадают с направлением обхода, поэтому будем считать их со знаком плюс. В контуре №2 ток I2 совпадет с направлением обхода, поэтому будет со знаком плюс, а ток I3 направлен в другую сторону, поэтому будет со знаком минус. Запишем второй закон Кирхгофа для контура №1:
Постоянный ток: законы Кирхгофа
При решении задач на законы Кирхгофа лучше придерживаться определенного алгоритма: 1. определить число неизвестных токов – столько уравнений должно быть в системе ; 2. определить количество узлов – уравнений по первому закону тогда нужно составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто хочет разобраться досконально – есть видео.
Задача 1. Два элемента с В и В соединены по схеме, показанной на рисунке . Сопротивление Ом. Внутреннее сопротивление элементов одинаково Ом. Определить силу тока, идущего через сопротивление .
К задаче 1
Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:
Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:
Будем обходить второй контур по часовой стрелке:
Неизвестных токов – три, мы составили три уравнения. Этого достаточно, чтобы найти токи:
Выразим из второго уравнения, а – из третьего:
Подставим эти выражения в первое уравнение:
Тогда токи и
Ответ: A, A, A. Задача 2. Найти силу тока на всех участках цепи‚ если В, В‚ В, Ом‚ Ом‚ Ом‚ Ом‚ Ом, Ом.
К задаче 2
Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас два узла, поэтому уравнение будет одно. Затем, обходя контуры, составим два уравнения по второму закону: их нужно составить два, так как неизвестных токов в цепи три.
Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора): , , .
Ответ: , , .
Задача 3. В схеме, показанной на рисунке, найти силу тока через гальванометр, если В, кОм; В, кОм. Сопротивлением гальванометра пренебречь.
К задаче 3
Нам неизвестно сопротивление гальванометра, запишем для напряжения на нем два уравнения:
Приравнивая, получим
Заметим, что, если , то равенство будет выполнено. Таким образом, ток через гальванометр не течет.
Ответ: .
Задача 4. В цепи В‚ В, Ом, Ом. Найти распределение токов в цепи. Внутреннее сопротивление источников тока не учитывать.
К задаче 4
Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас три узла, поэтому уравнений будет два. Затем, обходя контуры, составим три уравнения по второму закону: их нужно составить именно три, так как неизвестных токов в цепи шесть.
Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора): , , , , , .
Ответ: , , , , , . Задача 5. Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.
К задаче 5
Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неизвестных токов шесть и система должна состоять из шести уравнений.
Чтобы воспользоваться калькулятором, я задала Ом и В. В итоге получилось: , , , , , .
Минусы свидетельствуют о противоположном направлении тока в этой ветви тому, что мы нарисовали.
Задачи на правило Кирхгофа с решением
Мы уже писали про закон Ома, а также параллельное и последовательное соединение проводников. Но это были цветочки. Сегодня разберемся с задачами посложнее: посмотрим, как решаются задачи на правила Кирхгофа.
Не забывайте подписаться на наш телеграм-канал: там вас ждут актуальные новости сферы образования, полезные лайфхаки и скидки для студентов.