Законы Ома и Кирхгофа в комплексной форме.
Введение понятий комплексного сопротивления и комплексной проводимости означает, по-существу, введение закона Ома в комплексной форме для установившегося синусоидального режима
или.
Комплексная амплитуда напряжения на зажимах пассивного двухполюсника равна комплексной амплитуде тока, умноженной на комплексное сопротивление двухполюсника.
Пример 1.
Через зажимы двухполюсника с комплексным сопротивлением Z=40ej30 Ом протекает синусоидальный ток i =3 Sin (314 t + 15o) A. Определить напряжение u(t) на зажимах двухполюсника.
Решение.
Находя комплексную амплитуду тока и зная комплексное сопротивление двухполюсника, на основании закона Ома в комплексной форме определяем комплексную амплитуду напряжения
Следовательно, мгновенное напряжение равно u=120 Sin (314 t + 45o), B.
Первый закон Кирхгофа в комплексной форме: Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.
.
Поскольку каждое слагаемое в представленном выражении есть вектор, то результат есть сумма векторов. Это обстоятельство позволяет контролировать аналитические расчеты наглядными графическими построениями — векторными диаграммами.
Пример 2
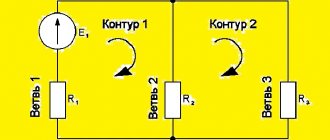
. В узле электрической цепи сходятся 3 ветви с синусоидальными токам одной частоты (рис.3.3,а).
Мгновенные значения токов i 2 и i 3 определяются выражениями i2= 100 Sin( 100t-45o) и i3= 50 Sin( 100t+30o). Требуется определить ток i1, пользуясь методом комплексных амплитуд.
Решение.
На основании первого закона Кирхгофа в комплексной форме находим
, где ,
Тогда
Построив вектора токов на комплексной плоскости (рис.3.3,б), убеждаемся, что сумма их действительно равна 0.
Переходя от комплекса к мгновенному значению, получим i1= 101 Sin(100t-74o), А.
Второй закон Кирхгофа в комплексной форме — в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом:
.
Пример 3
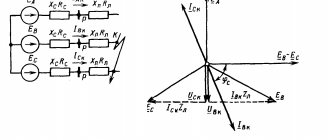
. Известны мгновенные значения напряжений на элемен-тах контура ( рис.3.4,а) u1= 10 Sin( 100t-45o) B, u2= 25 Sin( 100t+30o)B, u3= 5 Sin( 100t+60o)B. Требуется определить мгновенное значение ЭДС источника напряжения.
Решение.
На основании второго закона Кирхгофа для мгновенных значений напряжений и ЭДС находим e = u1+ u2+ u3.
Переходя к комплексам, получим
, где
; ;
Следовательно,
=
Построив вектора напряжений на комплексной плоскости (рис.3.4,б) убеждаемся, что сумма их действительно равна вектору ЭДС. Переходя от комплекса к мгновенному значению, получим e = 32.3 Sin(100t+18o), В.
Метод комплексных амплитуд.
Метод комплексных амплитуд — метод расчета линейных радиотехнических цепей, содержащих реактивные элементы, в установившемся режиме при гармонических входных сигналах.
Суть метода заключается в следующем:
1) Для всех реактивных элементов определяется их комплексный импеданс.
2) Все токи и напряжения рассматриваются в виде комплексных амплитуд.
После введения этих замен задача анализа цепи сводится к задаче анализа цепи на постоянном токе:
— импедансы трактуются как обычные сопротивления;
— комплексные амплитуды токов и напряжений как обычные токи и напряжения.
Таким образом, мы избавились от реактивности
элементов и
зависимости от времени
сигналов. Эти факторы, затрудняющие математические операции при описании схемы, теперь перенесены в сигнал: все параметры зависят от частоты гармонического сигнала и являются комплекснозначными.
Задача анализа цепи на постоянном токе решается соответствующими методами, например, методом узловых потенциалов или методом контурных токов. После нахождения всех искомых комплексных амплитуд их можно при необходимости перевести обратно в гармонические сигналы.
Данный метод применяется для расчёта разветвлённых цепей переменного тока, содержащих реактивные сопротивления (конденсаторы и индуктивности). Сопротивления
этих элементов записываются через комплексные числа.
Сопротивление конденсатора будет равно: Zc=j/ωC,
сопротивление индуктивности: ZL=jωL,
где j – мнимая единица вместо i, так как через i обозначается ток,
ω – циклическая частота, которая равна 2πν,
C и L – соответственно ёмкость и индуктивность.
Источник напряжения с учётом фазы обозначается как Uejφ, где U – действующее напряжение, φ – фаза данного источника.
Если дан источник тока с определённой фазой, то из этой фазы вычитается π/2, чтобы получить фазу данного источника по косинусу, а затем через получившуюся фазу по косинусу данный источник записывается аналогично источнику напряжения: Iejφ.
Если последовательно резистору включён конденсатор, то их общее сопротивление записывается, как R-jZc, если индуктивность, то общее сопротивление равно R+jZL.
Затем в цепи условно выбираются направления токов, у источников напряжения и тока условно выбираются + и -, и составляются уравнения для расчёта данной цепи лучше всего по правилам Кирхгофа (первое правило Кирхгофа:
сумма токов во всех ветвях, сходящихся в данном узле равна нулю; в
торое правило Кирхгофа:
сумма падений напряжений на всех сопротивлениях равна сумме всех ЭДС в данном контуре) или по методу узловых потенциалов:
1) Закон Ома для участка цепи содержащего ЭДС:
φ1 φ2
φ1 – узел, от которого течёт ток;
φ2– узел, к которому течёт ток;
V1 – источник, включённый по направлению тока;
V2– источник, включённый противоположно направлению тока;
R1 – сопротивление ветви.
2) Закон сохранения заряд
:
Далее решая эту систему, получим комплексные значения токов в ветвях. Чтобы получить значения токов, которые будут показывать амперметры, нужно просто взять модули этих комплексных токов.
Пример:
Рассчитаем методом комплексных амплитуд с помощью правил Кирхгофа данную цепь.
Законы Кирхгофа и закон Ома в комплексной форме. Комплексное и полное сопротивление и проводимость
Рассмотрим произвольный контур электрической цепи (рис. 1.6).
Рис. 1.6 – Контур электрической цепи
Согласно второму закону Кирхгофа выполняется равенство:
. (1.33)
Воспользуемся соответствием (1.32) и перепишем данное равенство в виде:
или же
Поскольку данное равенство выполняется для любого момента времени , то знак вещественной части можно опустить:
или же
, (1.34)
то есть алгебраическая сумма комплексных амплитуд напряжений на элементах цепи, образующих контур, равна нулю. Это и составляет суть второго закона Кирхгофа в комплексной форме. Знак комплексной амплитуды, по-прежнему определяется совпадением или несовпадением направления напряжения с выбранным направлением обхода контура.
Аналогичным образом рассмотрим произвольный узел электрической цепи (рис. 1.7).
Рис. 1.7 – Узел электрической цепи
Согласно первому закону Кирхгофа выполняется равенство:
. (1.35)
Воспользуемся соответствием (1.32) и перепишем данное равенство в виде:
или же
Поскольку данное равенство выполняется для любого момента времени , то знак вещественной части можно опустить:
или же
, (1.36)
то есть алгебраическая сумма комплексных амплитуд токов ветвей, сходящихся в любом узле электрической цепи, равна нулю. Это и составляет суть первого закона Кирхгофа в комплексной форме. Знак комплексной амплитуды, по-прежнему определяется направлением соответствующего тока ветви: знак «+» соответствует притекающим к узлу токам, а знак «-» — оттекающим от узла токам.
Преобразуем аналогичным образом компонентные соотношения для сопротивления, индуктивности и емкости:
. (1.37)
Воспользуемся соответствием (1.32) и перепишем данные равенства в виде:
Поскольку операции взятия вещественной части, умножения на константу, дифференцирования и интегрирования являются линейными, то они являются перестановочными и данные равенства можно переписать в виде:
Поскольку данное равенство выполняется для любого момента времени , то знак вещественной части можно опустить. Тогда после выполнения операций дифференцирования и интегрирования данные выражения принимают следующий вид:
или же
. (1.38)
Данные выражения отражают суть закона Ома в комплексной форме: комплексная амплитуда напряжения на данном участке электрической цепи равна произведению комплексной амплитуды тока, протекающего по данному участку, и комплексного сопротивления данного участка.
Таким образом, комплексные сопротивления резистивного, индуктивного и емкостного элементов равны:
, , . (1.39)
При последовательном соединении элементов электрической цепи через них протекает один и тот же ток, а, значит, в выражения для закона Ома в комплексной форме будет входить одна и та же комплексная амплитуда тока. С другой стороны, напряжение на концах такого участка складывается из напряжений на отдельных элементах, а, значит, складываются и комплексные сопротивления этих элементов.
Величина, обратная комплексному сопротивлению, носит название комплексной проводимости. Очевидно, что при параллельном соединении элементов электрической цепи напряжение на их зажимах одинаково, а, значит, в выражения для закона Ома в комплексной форме будет входить одна и та же комплексная амплитуда напряжения. С другой стороны, ток, притекающий к такому соединению, складывается из токов, протекающих по каждому из соединенных элементов, а, значит, складываются и комплексные проводимости этих элементов.
Комплексные проводимости резистивного, индуктивного и емкостного элементов определяются выражениями:
, , . (1.40)
Введенные комплексные сопротивление и проводимость имеют определенный физический смысл. Так модуль комплексного сопротивления некоторого участка электрической цепи, который носит название полного сопротивления этого участка, определяет соотношение между амплитудой напряжения на данном участке и тока, протекающего по нему. Аргумент комплексного сопротивления определяет сдвиг фаз между напряжением на данном участке и током, протекающим по нему.
Рассмотрим примеры расчета линейных электрических цепей в рамках метода комплексных амплитуд.
ПРИМЕР 1
Определим в общем виде амплитуды и начальные фазы напряжений на сопротивлении и индуктивности для следующей электрической цепи:
Анализируемую цепь можно рассматривать в качестве двухполюсника, состоящего из последовательно соединенных сопротивления и индуктивности, к которому присоединен источник ЭДС.
Комплексное входное сопротивление этого двухполюсника равно:
.
По закону Ома находим комплексную амплитуду тока в цепи и напряжений на отдельных ее элементах:
,
где — аргумент комплексного входного сопротивления,
, (П1.1)
. (П1.2)
ПРИМЕР 2
Определим в общем виде амплитуды и начальные фазы напряжений на сопротивлении и емкости для следующей электрической цепи:
Цепь представляет собой двухполюсник, состоящий из последовательно соединенных сопротивления и емкости, к которому присоединен источник ЭДС.
Комплексное входное сопротивление этого двухполюсника равно:
.
По закону Ома находим комплексную амплитуду тока в цепи и напряжений на отдельных ее элементах:
,
где — аргумент комплексного входного сопротивления,
, (П2.1)
. (П2.2)
ПРИМЕР 3
Определим в общем виде амплитуды и начальные фазы напряжений на сопротивлении, индуктивности и емкости для следующей электрической цепи:
Находим комплексное входное сопротивление:
, или же
,
где – реактивная составляющая комплексного входного сопротивления.
По закону Ома находим комплексную амплитуду тока в цепи и напряжений на отдельных ее элементах:
,
где — аргумент комплексного входного сопротивления,
, (П3.1)
, (П3.2)
. (П3.3)
3
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот…
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: