Закон Ома
После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями. Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Закон Ома для полной цепи – определение и формула
Закон Ома показывает отношения между напряжением (V), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
V = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
Видоизменения закона Ома.
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Георг Симон ОмЕсли надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома — основа электротехники
Это основное уравнение, используемое для изучения электрических цепей, было получено экспериментальным путем Георгом Симоном Омом. Он родился в Эрлангене Германии в 1787 году и поступил в университет этого города в 1805 году, где он получил докторскую степень. Георг преподавал математику в школах и проводил эксперименты по физике в школьной физической лаборатории, пытаясь понять принципы электромагнетизма.
В 1827 году он опубликовал статьи, в которых описана математическая модель того, как контуры проводят тепло в работах Фурье. Ом получил экспериментальные данные, на базе которых впервые смог сформулировать свой закон 8 января 1826 года. Он установил, что разность потенциалов между двумя точками в цепи равна произведению тока между ними на общее сопротивление всех электрических устройств. Чем больше напряжение батареи или ее общая разность электропотенциалов, тем больше будет ее ток. Аналогично, с большим сопротивлением он будет меньше.
Но его исследования не нашли должного понимания и Георг оставил свою работу в Кельне. Только в 1833 году он получил должность профессора в Нюрнберге. Выводы Ома послужили катализатором для новейших исследований по электричеству. В 1841 году ученого наградили медалью Копли, а в 1872 году «Ом» был принят в качестве единицы сопротивления в электрических цепях.
Закон Ома для полной электрической цепи описывает протекание тока через проводящие металлы, когда применяются различные уровни напряжения. Некоторые материалы, такие как электропровода, имеют небольшое сопротивление току — этот тип материала называется проводником.
Важно! В других случаях материал может препятствовать протеканию тока, но, тем не менее, допускает его использование. В электрических цепях эти компоненты часто называют резисторами. Существуют материалы, которые практически не пропускают ток, они называются изоляторами.
Что можно понимать под «Законом Ома»?
Закон Ома в дифференциальной и интегральной форме является эмпирическим соотношением, которое точно описывает проводимость подавляющего большинства проводниковых материалов. Однако некоторые материалы не подчиняются закону Ома, называются они «неомическими». Закон был назван в честь ученого Георга Ома, который опубликовал его в 1827 году. Он описывает измерения напряжения и тока с помощью простых электрических цепей, содержащих различные длины провода. Ом объяснил свои экспериментальные результаты с несколько более сложным уравнением, чем современная форма выше.
Понятие закона Ома в диф. форме также применяется для обозначения различных обобщений, например, векторная форма его используется в электромагнетизме и материаловедении:
J=σE,
где J — количество электрических частиц в конкретном месте резистивного материала, е — электрическое поле в этом месте и σ (сигма)- это материал, зависящий от параметра проводимости. Густав Кирхгоф сформулировал закон именно так.
Формула закона Ома
Первый Закон Ома устанавливает, что разница потенциалов между двумя точками резистора пропорциональна току. Более того, согласно этому закону, соотношение между потенциалом и током всегда является постоянным для омических резисторов.
V = RI, где:
V — напряжение/электропотенциал (В);
R — электросопротивление (ом);
I — электрический ток.
Формула
В нем U является скалярной величиной и меряется в (В). Разница в электропотенциалах между двумя точками цепи, указывает на наличие электросопротивления. Когда I проходит через резистивный элемент R, происходит падение электрического потенциала. Это различие возникает из-за рассеивания энергии, называемым эффектом Джоуля. I измеряет поток зарядов через тело в (А) и прямо пропорционален сопротивлению провода.
Второй закон Ома говорит о том, что электросопротивление R представляет собой свойство из тела, которое регулирует проходимость I. Это свойство зависит от геометрических факторов тела, таких как длина или площадь сечения участка и от вызываемой величины R. Его количество зависит исключительно от материала участка.
R= ρ*L/S, где:
R — электросопротивление (Ом);
ρ — удельное электросопротивление провода (Ом.м);
L — протяженность проводника (м);
S — площадь сечения провода (м²).
Омическим резистором называется любое тело, способное представлять постоянное сопротивление для данного диапазона напряжений. График напряжения как функция тока для омических резисторов является линейным. Резистор можно считать омическим в диапазоне, в котором его потенциал линейно возрастает с ростом I.
Сопротивление можно понимать как наклон линии, заданный тангенсом угла. Как известно, тангенс определяется, как отношение между противоположным и соседним сторонами, и, в случае, когда сопротивления омические, может быть рассчитан по формуле: R = U / I.
Треугольник
Чтобы помочь запомнить формулу, можно использовать треугольник с одной горизонтальной стороной и вершиной вверху, как пирамиду. Это иногда называют законом треугольника Ома. В верхнем его углу находится буква V, в левом углу — буква I, а в правом нижнем углу — R.
Обратите внимание! Чтобы использовать треугольник, прикрыть неизвестный параметр, а затем, рассчитать его из двух других. Если они находятся на одной линии, они умножаются, но если одна находится над другой, их следует разделить. Другими словами, если необходимо рассчитать I, напряжение делится на сопротивление, то есть V / R.
Где и когда можно применять закон Ома
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Важность закона Ома
Закон Ома в дифференциальной и интегральной форме, вероятно, являлся самым важным из ранних описаний физики электричества. Сегодня же мы считаем это почти очевидным, но, когда Ом впервые опубликовал свои работы, это было не так. Критики отнеслись к его трактовке с враждебностью. Они называли его работы «голыми фантазиями», а немецкий министр образования заявил, что «профессор, который проповедует такую ересь, недостоин преподавать науку».
Преобладающая в то время в Германии научная философия утверждала, что нет необходимости проводить эксперименты, чтобы развить понимание природы. Кроме того, брат Геогра, Мартин, математик по профессии, боролся с немецкой образовательной системой. Эти факторы препятствовали принятию работы Ома, и его работа не получила широкого признания до 1840-х годов. Тем не менее Ом получил признание за его вклад в науку задолго до его смерти.
Закон Ома в дифференциальной и интегральной форме представляет собой эмпирический закон, обобщение результатов многих экспериментов, которые показали, что ток примерно пропорционален напряжению электрического поля для большинства материалов. Он является менее фундаментальным, чем уравнения Максвелла, и подходит не во всех ситуациях. Любой материал будет разрушаться под силой достаточного электрического поля.
Закон Ома был соблюден на широком диапазоне шкал. В начале 20-го века закон Ома не рассматривался в атомном масштабе, однако эксперименты подтверждают обратное.
Электрическое сопротивление
Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.
Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.
Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.
Удельное сопротивление
Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:
Ёмкостное сопротивление
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.
Рисунок 2.
Мы можем использовать следующие соотношения:
Если $I(t)$ определена уравнением (1), то заряд выражен как:
где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac{pi }{2}.$ Амплитуда напряжения на емкости равна:
Величину $X_C=frac{1}{omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
Требуется консультация по учебной работе?Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос
Переход от интегральной формы закона Ома к дифференциальной
Найдем связь между вектором плотности тока ($\overrightarrow{j}$) и вектором напряженности электрического поля ($\overrightarrow{E}$) в одной и той же точке проводящей среды. Если вещество изотропно, то $\overrightarrow{j}\uparrow \uparrow \overrightarrow{E}$. Выделим в окрестности рассматриваемой точки гипотетический цилиндр, образующие которого параллельны векторам напряженности поля и плотности тока (рис.1).
Помощь со студенческой работой на тему Дифференциальная форма закона Ома
Курсовая работа 450 ₽ Реферат 280 ₽ Контрольная работа 210 ₽
Получи выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
Рис. 1
Через поперечное сечение цилиндра (dS) (рис.1) течет ток, сила которого запишется как:
Напряжение, приложенное к цилиндру можно выразить как:
где $E$ — напряжённость поля в рассматриваемой точке. Сопротивление цилиндра получит выражение:
Подставим формулы (3),(4),(5) в выражение (1), получим:
Проведем сокращения, получим:
Заменим удельное сопротивление ($\rho $), на удельную проводимость ($\sigma $). Используем то, что векторы напряженности и плотности тока имеют одинаковые направления окончательно запишем:
Уравнение (8) называется законом Ома в дифференциальной форме. В отличие от закона Ома в интегральной форме (1) уравнение (8) содержит величины, которые характеризуют электрическое состояние среды в точке.
Требуется вычитка, рецензия учебной работы? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос
Напряженность поля, которая входит в уравнение (8) — это поле внутри проводящей среды при наличии тока. Однако, если среда однородна, то в большинстве случаев это поле совпадает с электростатическим полем, то есть полем, которое было бы между электродами с таким же напряжением на них что и при наличии тока. Следовательно, в однородном проводнике линии напряженности электростатического поля совпадают с линиями тока.
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.
Рисунок 3.
Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
По условию $R=0. mathcal E$ самоиндукции можно выразить как:
Из выражений (8), (9) следует, что:
Амплитуда напряжения в данном случае равна:
где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).
Закон Ома для цепи
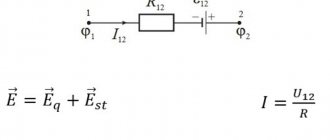
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит: Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Обобщённый закон Ома. Закон Ома для участка цепи
Закон Ома для участка цепи.
больше .Тогда закон Ома для данного участка цепи будет иметь вид:
Обобщенный закон Ома.
больше .
1) (источник ЭДС – генератор)
2) (источник ЭДС – двигатель)
Закон Ома для цепи, содержащей источник ЭДС (обобщенный закон Ома):
I=
Первый и второй законы Кирхгофа. Расчёт электричес-кой цепи по законам Кирхгофа ( на примере электрической цепи).
Первый закон Кирхгофа — алгебраическая сумма всех токов, сходящихся в узле равна нулю.
(Токи, направленные к узлу, условно принимаются отрицательными, а направленные от него -положительными). На
-I1-I2-I3+I4+I5=0
I1+I2+I3=I4+I5
Второй закон Кирхгофа — Вдоль замкнутого контура алгебраическая сумма падений напряжений в отдельных элементах контура равна алгебраической сумме ЭДС, входящих в этот контур (или 0, если контур не содержит ЭДС)
Пример расчета цепи, основанного законах Кирхгофа:
· Число уравнений по первому закону Кирхгофа равно числу узлов минус 1
1) I1-I2=0
2) -I1+I2=0
3) -I1+ I3+I4=0
· Число уравнений по второму закону Кирхгофа равно числу независимых контуров:
Последовательное, параллельное и смешанное соединение элементов.
А) Последовательное соединение – это такое соединение, при котором через все элементы протекает один и тот же ток I=I1=I2=I3 , при этом U=U1+U2+U3= I1R1+I2R2+I3R3=I*(R1+R2+R3). Где Rэкв= R1+R2+R3
I*Rэкв=U
При последовательном соединении все сопротивления можно заменить одним эквивалентным.
Б) Параллельное соединение – при нем все элементы присоединяются к одной паре узлов, т.е. находятся под одним напряжением. I1=U1/R1; I2=U2/R2; I3=U3/R , тогда I=I1+I2+I3. Тогда U/Rэкв=U1/R1+U2/R2+U3/R3 а значит 1/Rэкв=1/ R1+1/R2+1/ R3
, а
I=U/Rэкв
В) Смешанное соединение – такое соединение элементов, которое содержит последовательно и параллельно соединенные элементы. Rэкв=R1+R2+R6+R1R2R3/(R1R2+R2R3+R1R3)
Метод эквивалентных преобразований с одним источником.
Дано: R1, R2, R3, R4, R5,R6, E
Найти:
I.
R456=R4+R5+R6; R12=R1+R2; тогда преобразуем данную схему (рис.1) в эквивалентную (рис.2) с учетом этих преобразований.
R3456=(R3*R456)/(R3+R456). Исходя из этого преобразования преобразуем схему (рис.2) в эквивалентную (рис.3). I1=E/(R12+R3456)
I способ. Uab=E-I1R12; I2=Uab/R3; I3=Uab/R456.
II способ. В нем используется формула «разброса». I2=I1*R456/(R3+R456); I3=I1*R3/(R3+R456)
В случае, когда в электрической цепи имеется источник тока, то для определения тока, то для определения тока в ветвях можно использовать только формулу «разброса».
| Рис.1 |
| Рис.2 |
Метод контурных токов
уравнения метода контурных токов составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа . Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.
При составлении уравнений необходимо помнить следующее:
· — сумма сопротивлений, входящих в i-
й контур;
· — сумма сопротивлений, общих для i-
го и
k-
гоконтуров, причем ;
· члены на главной диагонали всегда пишутся со знаком “+”;
· знак “+” перед остальными членами ставится в случае, если через общее сопротивление i-
й и
k-
й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;
· если i-
й и
k-
й контуры не имеют общих сопротивлений, то;
· в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.
Пример расчета цепи методом контурных токов
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
;;
; .
Обойдя контур aeda,
по второму закону Кирхгофа имеем:
.Поскольку:
То:
Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров
Совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление. В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие. Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи. Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
Квантовое начало
Зависимость плотности тока от приложенного электрического поля имеет принципиально квантово-механический характер (классическая квантовая проходимость). Качественное описание закона Ома может быть основано на классической механике с помощью модели Друде, разработанной немецким физиком Паулем Друде в 1900 году. Из-за этого закон Ома имеет множество форм, например, так называемый закон Ома в дифференциальной форме.
Закон Ома для замкнутой цепи
Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:
I – Сила тока в цепи.
– Электродвижущая сила (ЭДС) – величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника. r – Внутреннее сопротивление источника питания.
Для электродвижущей силы внешнеее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I = /(R+r) .
Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.
Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания. С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы.
По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = – I*r.
Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U. Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах.
В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС (≈ U ) независимо от сопротивления внешней цепи R. Такой источник питания называют источником напряжения.
Формула закона Ома для замкнутой цепи
Выведем формулу закона Ома для замкнутой цепи.
Сторонние силы, перемещая заряд $Δq$ за время $Δt$, совершают работу:
$$А_{ст}=\mathscr{E}q$$
Ток, по определению, равен отношению заряда, прошедшего по проводнику ко времени прохождения, то есть:
$$I={Δq\over Δt}$$
Подставив значение заряда из этой формулы в предыдущую, получим:
$$А_{ст}=\mathscr{E}IΔt$$
Вся эта работа будет выделена в виде тепла на сопротивлении цепи. Сопротивление цепи состоит из двух компонент: сопротивление самой цепи $R$ и сопротивление источника ЭДС $r$. С учетом закона Джоуля-Ленца:
$$ А_{ст}=I^2RΔt+I^2rΔt$$
Приравнивая левые части формул, получаем:
$$\mathscr{E}IΔt=I^2RΔt+I^2rΔt$$
После сокращений и преобразований имеем:
$$I={\mathscr{E}\over R+r}$$
Сила тока в замкнутой цепи равна отношению ЭДС в замкнутой цепи к сумме сопротивления цепи и внутреннего сопротивления источника ЭДС.
Нелинейные элементы и цепи
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.
Закон Ома для мощности переменного тока
Известный треугольник закона Ома, используемый для цепей постоянного потока электронов, может использоваться только при переменном разряде, если нагрузка является чисто резистивной. Однако большинство систем содержат последовательные или параллельные комбинации сопротивления, емкости и индуктивности. Это приводит к несоответствию напряжения и разряда, и нагрузка становится сложной. В чисто емкостных системах форма волны разряда опережает форму волны напряжения, тогда как в индуктивных цепях интенсивность опережает разряд. В цепях, содержащих как катушки индуктивности, так и конденсаторы, форма сигнала не будет синфазной, кроме как в резонансе. Общим термином для сопротивления является полное сопротивление и обозначается символом Z. Треугольник полного сопротивления показан ниже:
Вам это будет интересно Особенности SMD конденсаторов
Треугольник
Треугольник используется точно так же, за некоторым исключением.
Следует отметить: при измерении напряжения или разряда измеритель будет показывать только правильные значения в ограниченном диапазоне частот. Обычно это справедливо для постоянного тока до 400 Гц, но это можно узнать, проверив спецификации прибора.
Для цепей, в которых напряжение и ток находятся только в фазе, может использоваться следующая круговая диаграмма.
Диаграмма
Закон Ома для участка цепи
Со школьного курса физики всем хорошо известна классическая трактовка Закона Ома: Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению.
I = U/R
Это значит, если к концам проводника сопротивлением R = 1 Ом приложено напряжение U = 1 Вольт, тогда величина тока I в проводнике будет равна 1/1 = 1 Ампер.
Отсюда следуют ещё два полезных соотношения: Если в проводнике, сопротивлением 1 Ом, протекает ток 1 Ампер, значит на концах проводника напряжение 1 Вольт (падение напряжения).
U = IR
Если на концах проводника есть напряжение 1 Вольт и по нему протекает ток 1 Ампер, значит сопротивление проводника равно 1 Ом.
R = U/I
Вышеописанные формулы в таком виде могут быть применимы для переменного тока лишь в том случае, если цепь состоит только из активного сопротивления R. Кроме того, следует помнить, что Закон Ома справедлив только для линейных элементов цепи.
Предлагается простой Онлайн-калькулятор для практических расчётов. Закон Ома. Расчёт напряжения, сопротивления, тока, мощности.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
| Дано: | Решение: |
|
|
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Интересно почитать: инструкция как прозвонить транзистор.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц. Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
$I={∆q}/{∆t}$
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время. Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_{0}nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t={∆l}/{υ}$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:
$I={∆q}/{∆t}={q_{0}nS∆l·υ}/{∆l}=q_{0}nυS$
В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836). Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока. Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.
Закон Джоуля-Ленца
Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:
$Q=I^2Rt$
Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.
Из закона Джоуля — Ленца следует, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это используется в технике, например, для распыления металлов.
При параллельном соединении все проводники находятся под одинаковым напряжением, но токи в них разные. Из формулы ($Q=I^2Rt$) следует, что, так как, согласно закону Ома $I={U}/{R}$, то
$Q={U^2t}/{R}$
Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.
Если в формуле ($A=IUt$) выразить $U$ через $IR$, воспользовавшись законом Ома, получим закон Джоуля-Ленца. Это лишний раз подверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении. Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задачка простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.
Другие формы закона Ома
Закон Ома в дифференциальной форме является крайне важным понятием для электротехники/электроники, поскольку он описывает как напряжение тока, так и сопротивление. Все это взаимосвязано на макроскопическом уровне. Изучая электрические свойства на макро- или микроскопическом уровне, используется более связанное уравнение, которое можно назвать «уравнением Ома», имеющее переменные, которые тесно связаны со скалярными переменными V, I и R закона Ома, но которые являются постоянной функцией положения в проводнике.