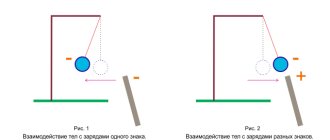
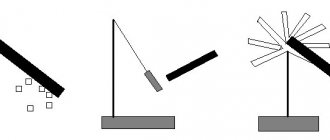
Общая информация
К основным параметрам последовательности импульсов относятся:
- l амплитуда импульса – Um,
- l длительность импульса – tu,
- l длительность паузы – tn,
- l период следования T или частота f = 1/T следования.
Если длительность tu всех импульсов, входящих в состав последовательности, и всех пауз tn постоянна в течение времени, то она называется периодической.
Важным параметром периодического импульсного процесса является скважность импульсов S. Скважность импульсов – это отношение периода следования к длительности импульса, рассчитывается по формуле:
Эффективность S при управлении устройства достигается при стабильной частоте сигнала. Иногда используют обратную величину D – коэффициент заполнения, рассчитывается по формуле:
При равенстве tu и tn скважность равна 2, и сигнал называется меандром. S и D – безразмерные величины, так как время делится на время. В цифровых устройствах применяются импульсы различной формы. Формой импульса называется графическое изображение закона изменения импульсного напряжения во времени. На рис. ниже показаны формы сигналов:
- а – прямоугольная,
- б – трапецеидальная,
- в – экспоненциальная,
- г – колокольная,
- д – ступенчатая,
- е – пилообразная.
Виды импульсных сигналов
Техническая характеристика формы импульсов связана с количественной оценкой основных параметров импульса, свойств отдельных его участков, которые играют разную роль при воздействии импульса на устройство. На рис. выше изображены идеализированные формы импульса. Из-за переходных процессов в устройствах (формирования и усиления импульсов) существует реальная форма, например, прямоугольного импульса (рис. ниже).
Реальная форма импульса
Основные параметры импульса – это:
- l Размах импульса – Um,
- l Длительность импульса – tи,
- l Длительность переднего фронта – tф,
- l Длительность заднего фронта – tсп,
- l Спад вершины – ΔU,
- l Размах выброса заднего фронта – Um обр,
- l Длительность выброса заднего фронта – tи обр.
Указанные величины считываются между уровнями 0.1 и 0.9 от амплитуды в микросекундах, в зависимости от частоты сигнала. Амплитудные – в вольтах.
Определить параметры импульсного сигнала можно с помощью осциллографа, частотомера или мультиметра.
Импульсы и запускающие сигналы (триггеры)
Общая характеристика импульсного сигнала
Виды импульсных сигналов. Под импульсной техникой понимают область радиоэлектроники, изучающую формирование импульсных сигналов и их прохождение через электрические цепи. Импульсный сигнал может состоять из одного или серии импульсов. Под импульсом понимают быстрое появление и исчезновение тока или напряжения, т. е. кратковременное действие тока или напряжения на электрическую цепь или устройство. В импульсной технике различают два вида импульсных сигналов — видеоимпульсы
(рис. 1, а), представляющие собой кратковременные односторонние (относительно оси времени) изменения напряжения или тока в цепи постоянного тока, и
радиоимпульсы
(рис. 1, б)—сигнал, состоящий из высокочастотных колебаний напряжения или тока, огибающая которых повторяет форму видеоимпульса. В импульсной технике в основном рассматривают видеоимпульсы.
Форма импульсов
Импульсы могут иметь прямоугольную, трапецеидальную, колоколообразную, треугольную и экспоненциальную
Рис. 1. Одиночные импульсы: а — видеоимпульс, б — радиоимпульс
форму (рис. 2). В импульсе различной формы различают фронт, вершину и спад. Импульсы могут быть положительной или отрицательной полярности. Импульсы положительной полярности на графиках изображают выше горизонтальной оси времени, а отрицательной — ниже оси.
Параметры импульсов. Каждый импульс характеризуется амплитудой А
(см. рис. 1, а), длительностью импульса
t
и, длительностями фронта
t
ф, спада
t
с, снижением вершины Δ
А,
а также мощностью в импульсе
Р
и.
Рис. 2. Формы импульсов: а — прямоугольная, б — трапецеидальная, в — колоколообразная, е — треугольная, д —экспоненциальная
Амплитуда
однополярного импульса характеризуется величиной (размахом) напряжения или тока от нуля до максимального значения импульса данной формы. В двустороннем импульсе величина от вершины положительного до вершины отрицательного импульса называется
полным размахом импульса
(полной амплитудой
A
п).
Длительность импульса
t
п — интервал времени, в течение которого ток или напряжение действует на электрическую цепь. В реальных схемах искажается форма импульсов, поэтому длительность определяют на уровне 0,1
A
и реже по основанию импульса. Активную длительность импульса
t
и.a измеряют на уровне 0,5
А.
Длительность фронта t
ф и спада
tc
оценивается интервалом времени, в течение которого амплитуда импульса нарастает от 0,1 до 0,9 своего максимального значения и падает от 0,9
A
до 0,1
А.
В большинстве случаев желательно иметь минимальные
t
ф и
to.
Снижение вершины ΔА
практически не должно превышать (0,01—0,05)
А.
Мощность в импульсе характеризуется отношением энергии W, выделенной в цепи при прохождении импульса, к его длительности t
и:
Для периодической последовательности импульсов (рис, 3, а)
свойственно следование импульсов через равные промежутки времени. Ее характеризуют следующие параметры.
Период следованияТ
и — интервал времени от момента появления одного импульса до момента появления следующего импульса той же полярности.
Частота следования
F
и
,
являющаяся величиной, обратной периоду следования, т. е.
Длительность паузы
Т
и
—
время между моментом окончания одного импульса и началом другого:
Скважность импульсов Q,
определяемая как отношение периода следования
Т
и к длительности
t
и
Среднее значение импульсного тока (напряжения) получается, если ток (напряжение) импульса равномерно распределить на весь период так, чтобы площадь прямоугольника I
ср
T
и (рис. 3,б) была равновелика площади импульса
Sи
| Коэффициент заполнения — величина, обратная скважности, показывающая, какую часть периода занимает импульс: |
| Рис. 3. Периодическая последовательность импульсов:а — прямоугольных, б — колоколообразных |
Средняя мощность PСр определяется отношением энергии W,
выделенной в цепи за период следования импульса Tи, к длительности этого периода:
Очевидно, Р
ср
Т
и=
P
и
t
и, откуда
Электронные приборы для импульсных схем очень часто выбирают по средней мощности.
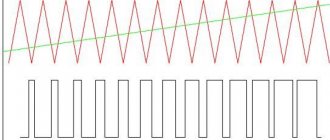
Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.
Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.
С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени. То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени. Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.
· Однополярные сигналы
— это электрические сигналы, которые всегда положительные или всегда отрицательные, не пересекающие горизонтальную ось. К однонаправленным сигналам относятся меандр, тактовые импульсы и запускающие импульсы.
· Двухполярные сигналы
— эти электрические сигналы также называют чередующимися сигналами, так как они чередуют положительные значения с отрицательными, постоянно пересекая нулевое значение. Двухполярные сигналы имеют периодическое изменение знака своей амплитуды. Наиболее распространенным из двунаправленных сигналов, является синусоидальный.
Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:
· Период
— это отрезок времени, через который сигнал начинает повторяться. Это временное значение также называют
временем периода
для синусоид или
шириной импульса
для меандров и обозначают буквой
T
.
· Частота
— это число раз, которое сигнал повторяет сам себя за период времени равный
1
секунде. Частота является величиной, обратной периоду времени, ( ). Единицей измерения частоты является Герц (
Гц
). Частотой в
1Гц
, обладает сигнал, повторяющий
1
раз за
1
cекунду.
· Амплитуда
— это величина изменения сигнала. Измеряется в Вольтах (
В
) или Амперах (
А
), в зависимости от того, какую временную зависимость (напряжения или тока) мы используем.
Периодические сигналы
Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц
.
Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом
. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.
Период может изменяться от долей секунды до тысяч секунд, так как он связан с его частотой. Например, синусоидальный сигнал, которому требуется 1
секунда для совершения полного цикла, имеет период равный одной секунде. Аналогично, для синусоидального сигнала, которому требуется
5
секунд для совершения полного цикла, имеет период равный
5
секундам, и так далее.
Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала
и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов
T
в секунду, как показано на рисунке ниже.
Синусоидальный сигнал
Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).
Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360°
(
Т = 360°
), или, если в радианах, то (
T =
).
Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.
Соотношения между периодом сигнала и его частотой:
Гц
c
Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц
,
МГц, ГГц
и даже
ТГц
| Префикс | Определение | Запись | Период |
| Кило | тысяча | кГц | 1 мс |
| Мега | миллион | МГц | 1 мкс |
| Гига | миллиард | ГГц | 1 нс |
| Тера | триллион | ТГц | 1 пс |
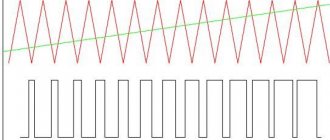
Меандр
Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.
Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения
периода.
Для меандра, время заполнения равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T
), то частота меандра:
Например, для сигнала с временем заполнения равным 10 мс, его частота равна:
Гц
Меандры используются в цифровых системах для представления уровня логической «1
» большими значениями его амплитуды и уровня логического «
0
» маленькими значениями амплитуды.
Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным
сигналом. В случае, или если время положительной части периода сигнала мало, то такой сигнал, является
импульсом
.
Прямоугольный сигнал
Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные
сигналы.
В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.
На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.
Отношение периода повторения сигнала , к длительности положительного импульса , называют скважностью:
Величину обратную скважности называют коэффициентом заполнения (duty cycle
):
Пример расчета
Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%. Необходимо найти частоту этого сигнала.
Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).
Гц
Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала. Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку. Отличным примером этого является использование широтно-импульсной модуляции
в регуляторах скорости. Термин
широтно-импульсная модуляция (ШИМ)
буквально и означает «изменение ширины импульса».
Треугольные сигналы
Треугольные сигналы, как правило, это двунаправленные несинусоидальные сигналы, которые колеблются между положительным и отрицательным пиковыми значениями. Треугольный сигнал представляет собой относительно медленно линейно растущее и падающее напряжение с постоянной частотой. Скорость, с которой напряжение изменяет свое направление равна для обоих половинок периода, как показано ниже.
Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.
В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал
.
Пилообразный сигнал
Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.
Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным. Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f
) и четных гармоник. Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.
Импульсы и запускающие сигналы (триггеры)
Хотя, технически, запускающие сигналы и импульсы два отдельных типа сигналов, но отличия между ними незначительны. Запускающий сигнал — это всего лишь очень узкий импульс. Разница в том, что триггер может быть как положительной, так и отрицательной полярности, тогда как импульс только положительным.
Форма импульса, или серии импульсов, как их чаще называют, является одним из видов несинусоидальной формы сигналов, похожей на прямоугольный сигнал. Разница в том, что импульсный сигнал определяется часто только коэффициентом заполнения. Для запускающего сигнала положительная часть сигнала очень короткая с резкими ростом и спадом и ее длительностью, по сравнению с периодом, можно пренебречь.
Очень короткие импульсы и запускающие сигналы предназначены для управления моментами времени, в которые происходят, например, запуск таймера, счетчика, переключение логических триггеров а также для управления тиристорами, симисторами и другими силовыми полупроводниковыми приборами.
Остальные типы сигналов, обычно, получают их комбинацией или модуляцией (изменением параметров, используя другой сигнал), например:
· Амплитудно-модулированный сигнал
· Частотно-модулированный сигнал
· Фазо-модулированный сигнал
· Фазо-частотно-модулированный сигнал
· Фазо-кодо-манипулированный сигнал
Управление скважностью
Блокинг генератор: принцип работы
С помощью цифровых сигналов происходит управление разнообразными устройствами. Первое применение такого управления использовалось при передаче информации кодом Морзе. Сигнал передаётся короткими и длинными импульсами. Каждой букве соответствует определённый набор точек и тире. Сегодня этот метод управления используется для ШИМ-управления.
При изменении D (коэффициент заполнения) от 0 до 1 добиваются нужного напряжения на выходе электронного устройства. Таким образом, можно управлять оборотами двигателя, освещением, яркостью дисплея и т.д. При формировании прямоугольных импульсов используются специально разработанные микросхемы, например, NE555, NL494, КР1006ВИ1, IR2153, и микроконтроллеры: Arduino, AVR, SG2525A.
Для обеспечения надёжной работы управляемых устройств к параметрам импульсного сигнала предъявляются жестокие требования по их стабильности. Это достигается применением кварцевого генератора и хорошей переходной характеристикой схемы формирования управляющих импульсов.
И́МПУЛЬС ЭЛЕКТРИ́ЧЕСКИЙ
Рис. 1. Электрические импульсы разной формы: а – прямоугольный; б – трапецеидальный; в – экспоненциальный; г – колоколообразный; д – радиоимпульс; A – амплитуда; τи – длительность импульса; τиа – длит…
И́МПУЛЬС ЭЛЕКТРИ́ЧЕСКИЙ, кратковременное скачкообразное изменение электрич. напряжения или силы тока. И. э. тока или напряжения (преим. одной полярности), имеющие постоянную составляющую и не содержащие ВЧ-колебаний, называются видеоимпульсами. По характеру изменения во времени различают видеоимпульсы прямоугольной, пилообразной, трапецеидальной, колоколообразной, экспоненциальной и др. формы (рис. 1, а–г). Реальный видеоимпульс может иметь довольно сложную форму (рис. 2), которая характеризуется амплитудой $A$, длительностью τи (отсчитывается на заранее обусловленном уровне, напр. $0,1\, A$ или $0,5\, A$), длительностью фронта τф и спада τс (отсчитываются между уровнями $0,1\, A$ и $0,9\, A$), скосом вершины $ΔA$ (выражается в процентах от $A$). Наиболее широко используются прямоугольные видеоимпульсы, на основе которых формируются синхронизирующие, управляющие и информационные сигналы в вычислит. технике, радиолокации, телевидении, цифровых системах передачи и обработки информации и др. Пилообразные и экспоненциальные видеоимпульсы применяются, напр., в системах развёртки телевизоров, радиолокационных индикаторов, осциллографов, а также при формировании сложных радиолокационных сигналов с внутриимпульсной частотной модуляцией. Длительность видеоимпульсов составляет от долей секунды до десятых долей наносекунды.
Рис. 2. Видеоимпульс и его основные характеристики: A – амплитуда; a – вершина; ΔA – скос вершины; b – хвост; τф – длительность фронта; τи – длительно…
Помимо одиночных и нерегулярно следующих во времени потоков И. э. на практике используют периодич. последовательности, которые дополнительно характеризуют периодом $T$ или частотой повторения $f = T^{-1}$. Важным параметром периодич. последовательности И. э. является скважность (отношение периода повторения импульсов к их длительности). По частотному распределению И. э. характеризуются спектром, который получается в результате разложения временно́й функции, выражающей И. э., в ряд Фурье (для периодич. последовательности одинаковых импульсов) или интеграл Фурье (для одиночных импульсов).
И. э., представляющие собой ограниченные во времени (прерывистые) ВЧ- или СВЧ-колебания, огибающая которых имеет форму видеоимпульса (рис. 1, д), называются радиоимпульсами. Длительность и амплитуда радиоимпульсов соответствуют параметрам модулирующих видеоимпульсов; дополнит. параметром является несущая частота. Радиоимпульсы используют гл. обр. в устройствах радиотехники и техники связи; их длительность находится в пределах от долей секунды до нескольких наносекунд.
Видео
RS триггер
Кофе капсульный Nescafe Dolce Gusto Капучино, 3 упаковки по 16 капсул
1305 ₽ Подробнее
Кофе в капсулах Nescafe Dolce Gusto Cappuccino, 8 порций (16 капсул)
435 ₽ Подробнее
Hi-Res плееры
Форма и параметры импульсов
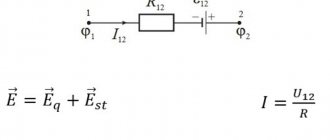
В импульсной технике применяются импульсы токов или напряжений самых различных форм. Основными идеализированными формами являются прямоугольные, трапецеидальные, треугольные, экспоненциальные и колокольные. При этом различают такие участки импульсов, как фронт, вершина, срез, основание и хвост. Основные параметры импульсов следующие (рис. 1.1): – амплитуда импульса; DI –
спад вершины импульса; t – длительность импульса; – длительность фронта; – длительность среза. Измерение длительностей как самих импульсов, так и их отдельных участков становится малоопределенным при работе с реальными импульсами, не имеющими простой геометрической формы (рис. 1.2). Поскольку определение временных параметров импульсов такой формы затруднительно, для характеристики формы реальных импульсов введено понятие об активных длительностях, определяющихся разностями соответствующих моментов времени, в которые импульс
i
(
t
) принимает значения и
.
Тогда временные параметры импульсов можно определить как междецильные интервалы:
; ; .
Рис. 1.2
Для импульсов, не имеющих явно выраженных фронта, среза и плоской части, вводится понятие длительности импульса на уровне , т. е. .
Прямоугольные импульсы, получаемые с помощью ФД или ОИЛ, имеют на своей вершине колебания, которые называются осцилляциями и чаще всего являются нежелательными. Неравномерность вершины определяется значением выброса импульса , который, в свою очередь, определяет пиковое значение импульса . При этом высота импульса , выражающая его номинальное значение, обычно определяется без учета осцилляций [4].
Средним значением последовательности импульсов, определяющим постоянную составляющую импульсного процесса, называется величина
.
Для последовательности прямоугольных импульсов тока с амплитудой Im
. (1.1)
Действующее значение последовательности импульсов тока произвольной формы
.
Для последовательности прямоугольных импульсов тока с амплитудой Im
. (1.2)
Из сопоставления формул (1.1) и (1.2) следует, что действующее значение параметров импульсного процесса больше его среднего значения в раз.
При генерировании в нагрузке импульсов произвольной формы среднее значение тока за время длительности импульса t
,
а действующее значение
.
На отрезке времени 0…t среднее и действующее значения импульсов произвольной формы могут быть представлены эквивалентными прямоугольными импульсами с амплитудами и . Тогда среднее и действующее значения тока нагрузки за период равны, соответственно,
и .
В тех случаях, когда в нагрузке генерируются импульсы полусинусоидальной формы, среднее и действующее значения тока за время t равны, соответственно,
, а .
Токи нагрузки за период частоты следования импульсов:
, (1.3)
. (1.4)
Отношение среднего и действующего значений тока
.
В ряде случаев, когда форма импульсов не является определяющей для электрофизического процесса, достаточно использовать полный разряд емкостного накопителя величиной C
, заряжаемого до максимального напряжения
Um
в паузу между импульсами. В резистивной нагрузке
R
будут генерироваться импульсы экспоненциальной формы, длительность которых теоретически равна бесконечности. Примем во внимание, что за время
t
³ 5
RC
практически вся энергия, запасенная в емкостном накопителе, реализуется в нагрузке, а длительность периода
T
>> 5
RC
. Тогда среднее значение тока нагрузки
. (1.5)
Действующее значение тока нагрузки I
дможно найти следующим образом. Средняя мощность, выделяемая в резистивной нагрузке,
.
Отсюда
. (1.6)
Введем понятие скважности для этого случая как
.
Тогда зависимость (1.4) примет вид
и из сопоставления (1.5) и (1.6) отношение действующего и среднего значений токов
.
Следует отметить, что на практике достаточно часто в цепь разряда емкостного накопителя включается дополнительная индуктивность L
для ограничения скорости нарастания тока силового коммутатора. При этом форма импульса отличается от экспоненциальной, а фронт импульса приобретает конечную длительность, отличную от нуля. Если выдерживается соотношение т. е. процесс разряда емкостного накопителя является апериодическим или критическим и происходит за отрезок времени, существенно меньший, чем длительность периода, то зависимости (1.5) и (1.6) остаются справедливыми. В тех случаях, когда , процесс разряда емкостного накопителя будет колебательным. При наличии коммутатора, обладающего вентильными свойствами, импульс тока нагрузки будет иметь форму, близкую к полусинусоидальной, и тогда для определения приближенных значений среднего и действующего токов могут быть использованы зависимости (1.3) и (1.4).