Закон Ома для неоднородного участка цепи

Неоднородный участок цепи постоянного тока

Определение основных параметров и процессов:

перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):

q = q0*n*V.

Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала. Чтобы компенсировать сопротивление, необходимо приложение дополнительных «сторонних» сил.

Пример неоднородного участка цепи

Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).

Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.

Ниже приведены формулы, характеризующие рассмотренный пример:

A12/q = ϕ1 – ϕ2;
Ast/q = E12;
U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
I = (ϕ1 – ϕ2 + E12)/ R.

Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.

К сведению. При выполнении расчетов следует учитывать действительную полярность источника постоянного тока. В зависимости от подключения соответствующая ЭДС будет способствовать или препятствовать перемещению заряда.

Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом. На выходе измерены потенциалы:

ϕ1= 20V; ϕ2=10V.

Подставив значения в формулу, можно получить нужный результат:

(20-10+40)/5 = +10А.

Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».

Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:

кулоновские – Fкул;
сторонние – Fc;
сопротивления кристаллической решетки – Fсп.

Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.

Московский государственный университет печати

Лекция 7. Замкнутые электрические цепи

7.1. Сторонние силы. Электродвижущая сила (ЭДС) и напряжение

7.2. Закон Ома для неоднородного участка цепи и замкнутой цепи. КПД источника тока

7.3 Правила Кирхгофа

7.1.

Сторонние силы. Электродвижущая сила (ЭДС) и напряжение

Рассмотрим, какими средствами можно поддерживать протекание тока, т.е. постоянное напряжение на концах проводника.

Пусть на концах проводника длиной l имеется разность потенциалов которая создает внутри него электрическое поле Е, направленное в сторону падения потенциала, т.к.

При этом в проводнике возникает электрический ток, который течет от большего потенциала к меньшему потенциалу . Обязательным условием существования тока является наличие разности потенциалов а для ее поддержания необходимо иметь устройство, с помощью которого будет происходить разделение электрических зарядов на концах проводника. Такое устройство называется источником тока.

В качестве источников тока используются гальванические элементы, аккумуляторы, термоэлементы, электрические генераторы.

Источник тока выполняет одновременно и вторую задачу — он замыкает электрическую цепь, по которой можно было бы осуществлять непрерывное движение зарядов. Ток течет по внешней части — проводнику и по внутренней — источнику тока.

Источник тока имеет два полюса: положительный с более высоким потенциалом и отрицательный с более низким потенциалом.

Разделение зарядов в источнике тока производится с помощью внешних, так называемых сторонних сил, направленных против кулоновских (электростатических) сил, действующих на разноименные заряды в проводниках самого источника тока.

Природа сторонних сил может быть самой различной: механической, химической, тепловой, биологической.

Если цепь, состоящая из проводника и источника тока, замкнута, то по ней проходит ток и при этом совершается работа сторонних сил .

Работа сторонних сил по перемещению единичного положительного заряда по замкнутой цепи называется электродвижущей силой (ЭДС):

Источник тока характеризуется величиной ЭДС и внутренним сопротивлением r. За направление действия ЭДС будем считать направление действия сторонних сил на положительные заряды.

Участок электрической цепи, на котором действуют сторонние силы, называют неоднородным.

Он содержит источник тока с ЭДС , внутренним сопротивлением r и нагрузку с сопротивлением R.

Полная работа, которую совершают кулоновские силы и сторонние силы при перемещении заряда по цепи, равна:

где — работа кулоновских сил, — работа сторонних сил.

Напряжением U на данном участке цепи называется величина, равная отношению суммарной работы, совершаемой при перемещении заряда , к величине этого заряда:

Или с учетом зависимостей и получаем:

напряжение на участке цепи равно сумме разности потенциалов и электродвижущей силы.

Напряжение на концах участка цепи равно разности потенциалов только в том случае, если на этом участке не действует ЭДС.

Направление действия ЭДС совпадает с направлением от «-» к «+» на символическом обозначении. Например, для замкнутой цепи на рис. 30 .

Выражение можно записать как

где I(R+r) — называется падением напряжения на сопротивлении (R+r).

При этом справедливо правило знаков: перед (или I) берется знак «+», если направление действия ЭДС (или направление тока) совпадает с направлением от 1 к 2, и наоборот.

Например, для участка цепи, изображенного на рис. 31 ,

7.2.

Закон Ома для неоднородного участка цепи и замкнутой цепи. КПД источника тока

Закон Ома для неоднородного участка цепи имеет вид:

Если электрическая цепь замкнута, то точки 1 и 2 совпадают, при этом и общее сопротивление всей цепи равно r+R, поэтому закон Ома для замкнутой цепи:

где — алгебраическая сумма всех ЭДС, приложенных в этой цепи.

Если цепь разомкнута, и, следовательно, в ней отсутствует ток (I=0), то Это значит, что ЭДС, приложенная в разомкнутой цепи, равна разности потенциалов на концах. Таким образом, для нахождения ЭДС источника тока следует измерить разность потенциалов на его клеммах при разомкнутой внешней цепи.

При последовательном соединении нескольких источников тока полная ЭДС батареи равна алгебраической сумме ЭДС всех источников, а суммарное сопротивление равно сумме сопротивлений, т.е.

При параллельном подключении n источников с одинаковыми ЭДС и внутренними сопротивлениями r суммарная ЭДС одного источника а внутреннее сопротивление

При прохождении электрического тока I по замкнутой цепи на всех ее участках выделяется мощность. Полная мощность, развиваемая источником, идет на выделение тепла во внешнем и внутреннем сопротивлениях, и равна:

Полезная мощность, которая выделяется на нагрузке R:

Если исследовать зависимость (R), то можно получить следующее: максимум функция принимает при условии равенства R = r.

Мощность, выделяемая во внутреннем сопротивлении, использована быть не может и называется теряемой мощностью.

Коэффициентом полезного действия (КПД) источника тока называется отношение полезной мощности к полной мощности:

При условии R=r, когда на нагрузке выделяется максимальная мощность, КПД = 1/2, и это не означает, что КПД максимален.

При максимальном значении тока в замкнутой цепи (короткое замыкание)

полезная мощность = 0, т.к. R=0 .

7.3.

Правила Кирхгофа

Если ЭДС источников различны, то для расчетов значений сил токов в различных участках разветвленной цепи удобно пользоваться правилами Кирхгофа.

Первое правило Кирхгофа.
Точка соединения нескольких проводников называется узлом. Алгебраическая сумма токов в узле равна нулю:
Токи, текущие к узлу, считают положительными, от узла — отрицательными.
Второе правило Кирхгофа.
Алгебраическая сумма падений напряжений на замкнутом контуре разветвленной цепи равна алгебраической сумме ЭДС:
Необходимо условиться о направлении обхода контура. Выбор этого направления совершенно произволен. Все токи , совпадающие по направлению с направлением обхода контура, считаются положительными. ЭДС источников тока, включенных в различных участках контура, считаются положительными, если они создают ток, направленный в сторону обхода контура.
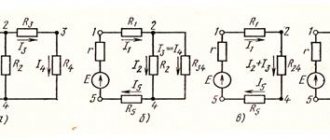
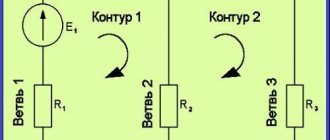
Например, для замкнутого контура АВСД (рис. 33 ) в случае обхода по часовой стрелке, уравнение Кирхгофа записывается следующим образом:

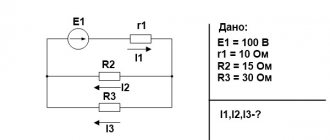
Задача на расчет токов в различных участках разветвленной цепи

Рассчитать токи во всех участках цепи, изображенной на рис. 33,б), если = 2В, = 4 В, Ом, R = 9 Ом.

Решение.

Выберем направление токов, как указано на рис. 33,б. Для узла А запишем первое правило Кирхгофа:

Рассмотрим замкнутый контур , R, направление обхода контура — против часовой стрелки. Запишем второе правило Кирхгофа:

Также для контура , R

Мы получили систему трех уравнений относительно трех неизвестных. Решим систему уравнений:

Окончательно получим: I = 0,3 А, = -0,35 А, = 0,65 А. Знак минус означает, что ток по участку цепи течет в направлении, обратном нами выбранному.

Контрольные вопросы и задачи

Приведите примеры сторонних сил. Где они действуют?
Чем определяется величина ЭДС источника тока?
Запишите закон Ома для неоднородного участка цепи.
Запишите закон Ома для замкнутой цепи.
Источник тока с ЭДС 6,4 В и внутренним сопротивлением 2 Ом питает три последовательно включенных лампочки сопротивлением 10 Ом каждая. Найти падение напряжения на каждой лампочке.
Как определяется коэффициент полезного действия источника тока?
Два одинаковых сопротивления подключаются к источнику тока последовательно и параллельно. В каком случае КПД будет больше?
Что называют напряжением на участке цепи?
Запишите правила Кирхгофа. Где они применяются?

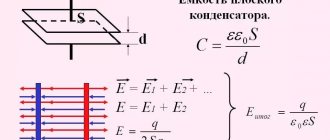
Закон Ома для замкнутой цепи

Закон Ома для участка цепи

В реальной ситуации следует учитывать электрические сопротивления нагрузки (Rн) и самого источника питания (Rи). Классическую формулу дополняют следующим образом:

I = E/(Rн+Rи).

Если в рассмотренный выше пример добавить Rи=1Ом, получится I = (ϕ1 – ϕ2 + E12)/(Rн+Rи) = (20-10+40)/(5+1) = +8,33А. Видно уменьшение силы тока в цепи, обусловленное увеличением общего электрического сопротивления. Чтобы компенсировать потери для подключения более мощной нагрузки, необходимо увеличить ЭДС источника.

Как звучит закон Ома для участка цепи

Ток в проводнике возникает в электрическом поле, которое, в свою очередь, появляется при наличии разности потенциалов или напряжения. Движение тока направлено в сторону меньшего потенциала. Условно считается, что в этом направлении двигаются положительные заряды, а в обратную сторону происходит движение свободных электронов.
На участке металлического проводника данный процесс будет выглядеть следующим образом. На каждом конце присутствует потенциал – ϕ1 и ϕ2, при этом ϕ1 > ϕ2. Следовательно, напряжение в этом месте равно U = ϕ1 – ϕ2. Немецкий ученый Ом практически установил зависимость, при которой с увеличением напряжения, возрастает и сила тока, протекающего через неполный участок.

Для каждого из проводников, отличающихся материалами, был построен свой график, отражающий зависимость силы тока от напряжения. В дальнейшем, эти графики стали известны, как вольт-амперные характеристики. В результате, было установлено наличие линейной связи между обеими величинами – силой тока и напряжением. То есть, они находятся в прямой пропорциональной зависимости.

Но, как показывают графики, все проводники обладают разными коэффициентами пропорциональности. Следовательно, у них разная степень проводимости, получившая название электрического сопротивления (R). Поэтому, чем ниже будет сопротивление проводника, тем выше сила тока, проходящего через него. При том, что напряжение для всех проводников будет одинаковым.

После всех опытов ученый смог окончательно сформулировать свой закон для участка цепи:

Сила тока в однородном проводнике на отдельном участке, находится в прямой пропорции с напряжением на этом же участке и в обратной пропорциональной зависимости с сопротивлением данного проводника.

Классическая формулировка

Закон Ома в дифференциальной форме

Для участка цепи без источника ЭДС достаточно использовать классический закон Ома:

I (сила тока) = U (напряжение) /R (электрическое сопротивление).

Данное соотношение было установлено экспериментальным путем в начале 19 века. В названии сохранена фамилия немецкого ученого, который сделал открытие. Напряжение определяют по разнице потенциалов на концах проводника:

U = ϕ1 – ϕ2.

Элементарные вычисления показывают взаимные зависимости перечисленных параметров:

I1 = 24/6 = 4А;
I2 = 60/6 = 10А.

Увеличив разницу потенциалов, при неизменном сопротивлении получают большую силу тока:

I2 > I1.

Чтобы уменьшить ток до нужного уровня, при работе с определенным источником питания изменяют сопротивление:

I1 = 24/4 = 6А;
I2 = 24/12 = 2А.

Основные формулы

Для запоминания правил пользуются такой картинкой. Чтобы вычислить определенный параметр, закрывают соответствующий сегмент. Взаимное расположение оставшихся компонентов условно изобразит необходимую формулу.

Ток, напряжение и сопротивление

Эта картинка наглядно демонстрирует взаимное влияние тех основных электрических параметров. С ее помощью можно пояснить особенности практического применения на примере типового проекта домашней сети питания.

В современных жилых объектах часто используют кондиционеры, духовые шкафы, другую технику с большой мощностью потребления. Для нормального функционирования требуется увеличивать ток, потому что напряжение ограничено стандартами. Повышающие трансформаторы в данном случае не пригодятся, так как серийные изделия рассчитаны на подключение к сети 220 (380) V.

При увеличении силы тока понадобятся проводники с достаточно большим поперечным сечением. В противном случае концентрация зарядов на единицу объема повысится до критичной величины. Воздействие на кристаллическую решетку повысит температуру металла вплоть до механического разрушения проводки.

Чтобы исключить проблемы, кроме кабельной продукции, тщательно выбирают защитные автоматы. Для создания проекта электроснабжения и перечня подходящих функциональных компонентов пользуются представленными выше формулами.

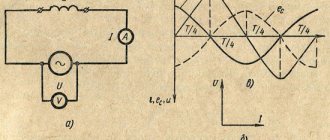
Закон Ома для переменного тока

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление. В таком случае запись Закона Ома будет иметь вид:

I = U/Z

Здесь Z – полное (комплексное) сопротивление цепи – импеданс. В него входит активная R и реактивная X составляющие. Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи. Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме: – комплексная амплитуда тока. = Iampe jφ – комплексная амплитуда напряжения. = Uampe jφ – комплексное сопротивление. Импеданс. φ – угол сдвига фаз между током и напряжением. e – константа, основание натурального логарифма. j – мнимая единица. Iamp , Uamp – амплитудные значения синусоидального тока и напряжения.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит: Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

Использование закона Ома при параллельном и последовательном соединении

При последовательном соединении элементы цепи подключаются друг за другом последовательно. Так как такая электрическая цепь является неразветвленной, сила тока на каждом ее участке будет одинаковая. Пример последовательного соединения — лампочки в новогодней гирлянде.

При последовательном соединении элементов основные параметры электроцепи рассчитываются следующим образом:

Где \(I\) — общая сила тока в электроцепи, \(I_1\) — сила тока первого участка, \(I_2\) — сила тока второго участка, \(I_3\) — сила тока третьего участка.

Где \(U\) — общее напряжение, \(U_1\) — напряжение первого участка, \(U_2\) — напряжение второго участка, \(U_3\) — напряжение третьего участка.

Сопротивление согласно формуле:

Где \(R\) — общее сопротивление в цепи, \(R_1\) — сопротивление первого участка, \(R_2\) — сопротивление второго участка, \(R_3\) — сопротивление третьего участка.

Подключая элементы в цепь параллельно, получают разветвленную электрическую цепь. Примером такого соединения является стандартная разводка электричества по квартире, когда в комнате одновременно можно включить несколько предметов бытовой техники и верхнее освещение.

При параллельном соединении элементов основные параметры электроцепи рассчитываются следующим образом:

Где \(I\) — общая сила тока в электроцепи, \(I_1, I_2, I_3\) — сила тока первого, второго и третьего участков соответственно.

Где \(U\) — общее напряжение, \(U_1, U_2, U_3\) — напряжение первого, второго и третьего участков соответственно.

Где \(R\) — общее сопротивление в цепи, \(R_1, R_2, R_3\) — сопротивление первого, второго и третьего участков соответственно.