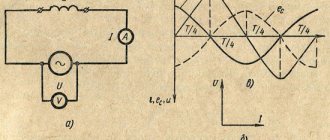
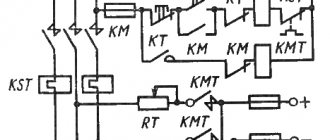
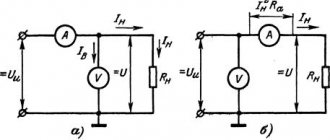
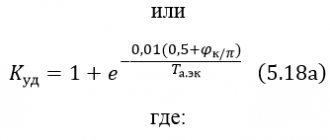Расчет электрических цепей методом эквивалентных сопротивлений (метод свертывания цепи)
Метод эквивалентных сопротивлений применяется для расчета таких электрических цепей, в которых имеются пассивныеэлементы, включенные между собой последовательно, параллельно или по смешанной схеме. Метод заключается в последовательной замене отдельных групп сопротивлений одним эквивалентным до получения самой простой схемы (см. рис. 13г). Затем определяется каждый ток в цепи.
Рисунок 13. Метод свертывания цепи
Определение эквивалентных сопротивлений
Обратимся к схеме, приведенной на рисунке 13а. Сопротивления и соединены последовательно. Поэтому . Эти два сопротивления можно заменить одним (эквивалентным) , тогда схема упростится (рисунок 13б).
Сопротивления и включены параллельно и их можно тоже заменить одним эквивалентным: .
Тогда схема еще упростится ( рисунок 13в).
В схеме на рисунке 13в сопротивления , и включены последовательно и могут быть заменены одним эквивалентным . Схема еще более упростится (рисунок 13г).
Подобными преобразованиями схему смешанного соединения пассивных элементов с одним источником энергии в большинстве случаев можно привести к простейшей схеме (рисунок 13г). В более сложных схемах методом эквивалентных сопротивлений достигается упрощение, которое значительно облегчает дальнейший расчет.
Определение токов
Определение начинается с простейшей схемы (рисунок 13г).
По закону Ома: т.к. ; .
Зная легко найти и . .
Задача 1
= 20 Ом , =30 Ом, = 12 Ом, = 8 Ом, = 1,5 Ом, = 160 В, = 0,5 Ом. Определить токи во всех элементах схемы и КПД источника (рисунок 13а).
Задача 2
Ток = 3 А. Величины сопротивления те же. Определить ЭДС и мощность источника (рисунок 13а).
Метод преобразования треугольника и звезды сопротивлений
Пассивные элементы в электрических цепях соединяются не только последовательно и параллельно. В ряде схем можно выделить группы из трех элементов, образующих треугольник или звезду сопротивлений, которые не могут быть рассчитаны методом свертывания.
При расчете подобных цепей сначала проводят преобразование треугольника сопротивлений в эквивалентную звезду или наоборот, а потом к преобразованной схеме применяют метод свертывания.
Рассмотрим схему измерителя величины сопротивлений (рисунок 14а). В этой схеме нет элементов, соединенных последовательно или параллельно, но имеются замкнутые контуры из трех сопротивлений (треугольники сопротивлений).
К узловым точкам a,b,c присоединен треугольниксопротивлений и . Его можно заменить по определенным правилам эквивалентной трехлучевой звездой, присоединенной к тем же точкам a,b,c (рисунок 14б).
Рисунок 14. Преобразование треугольника и звезды сопротивлений
Преобразование треугольника сопротивлений в эквивалентную звезду
Замена треугольника сопротивлений эквивалентной звездой и наоборот осуществляется при условии, что такая замена не изменит потенциалов узловых точек a, b, c и режим работы остальной части схемы не изменится (не изменятся токи, напряжения и мощности).
Рассмотрим схемы на рисунках 14в) и 14г). Эти схемы должны быть эквивалентны для всех случаев, и в частности для тока При этом в схеме треугольника между точками b и c включены две параллельные ветви с сопротивлениями Общее сопротивление между этими точками:
В схеме звезды между точками b и c включены последовательно сопротивления и .
Поэтому: .
Полагая , а затем аналогично получим:
;
Решив эту систему из трех уравнений, получим: ;
Преобразование звезды сопротивлений в эквивалентный треугольник
В той же исходной схеме заменим звезду, образованную сопротивлениями и на треугольник проводимости (рисунок 15а).
Рисунок 15. Преобразование звезды сопротивлений в эквивалентный треугольник
Задача
Определить токи в схеме, изображенной на рисунке 15а), если
= 12 Ом, = 18 Ом, = 6 Ом, =18 Ом, =18 Ом, =132 В.
Контрольные вопросы
1. В чем состоит метод свертывания электрической цепи?
2. Расскажите о преобразовании треугольника сопротивлений в эквивалентную звезду сопротивлений.
3. Расскажите о преобразовании звезды сопротивлений в эквивалентный треугольник сопротивлений.
Пример расчета схемы с определением потенциалов ее точек относительно произвольно выбранной
«общей точки» («земли»).
Расчет схемы предполагает кроме определение всех токов, протекающих в схеме, вычисление потенциала каждой точки схемы относительно «общей точкой» (ОТ). Иногда ОТ называют еще «землей» или «заземлением». В электрической схеме одна из точек схемы выбирается ОТ, т.е. потенциал ее условно принимается равным нулю. Обычно эта точка соединяется с корпусом прибора или с нулевым проводом электрической сети. В начале расчета не всегда ясно, какую именно точку схемы следует выбрать ОТ и в процессе расчета приходится неоднократно определять потенциалы всех точек относительно той или иной ОТ. Рассмотрим, как нужно поступать, чтобы минимизировать вычисления.
Например, нужно рассчитать схему, приведенную на рисунке 16, т.е. определить токи, протекающие во всех ветвях и определить потенциалы всех точек схемы относительно ОТ, которой в данном примере может быть выбрана либо точка F , либо точка D.
Рисунок 16. Исходная схема Рисунок 17
Исходные данные для расчета: R1=1 Ом; R2= R3=2 Ом;
R4=3 Ом; R5=1,2 Ом; R6=1,4 Ом; R7=6 Ом; Е=4,5 В.
Расчет токов осуществим методом эквивалентных сопротивлений и первым шагом заменим сопротивления R3, R4 и R5 одним эквивалентным сопротивлением R3-5 (Рисунок 17).
; R3-5=0,6 Ом.
Включенные последовательно сопротивления R3-5 и R6 заменим эквивалентным R3-6 (Рисунок 18). R3-6= R3-5 + R6=2 Ом.
Включенные параллельно сопротивления R3-6 и R7 заменим эквивалентным R3-7 (Рисунок 19). R3-7=
Рисунок 18 Рисунок 19
Рассчитаем величины токов в схеме, используя схемы на рисунках 16-19.
Ток I1 (Рисунок 19): I1=
Напряжения:
Токи (Рисунок 18):
Напряжение (Рисунок 17)
Токи (Рисунок 16):
.
Вычислять потенциалы точек легко в схеме, элементы которой включены последовательно (Рисунок 19). Вычислим потенциалы точек схемы в предположении, что ОТ является точка F, т.е. . Тогда при обходе контура по направлению протекания тока I1 получим:
=0.
Потенциал точки D вычисляется по схеме рисунка 17:
.
По результатам расчетов построим потенциальную диаграмму (рисунок 20). По вертикали отложим вычисленные потенциалы, а по горизонтали – величины сопротивлений в порядке, показанном на рисунке 20.
Рисунок 20. Потенциальные диаграммы точек схемы
Потенциальная диаграмма представляет собой прямую линию ABCF, тангенс угла наклона которой к оси сопротивлений представляет собой (по закону Ома для участка цепи) ток I1 (рисунок 19). Потенциальная диаграмма участка схемы, по которому протекает ток I6 (рисунок 18), представлен линией CDF.
Если теперь принять точку D общей ( , то согласно рисунку 17, потенциалы всех точек относительно ее:
;
.
Потенциальная диаграмма точек схемы рисунка 19 в этом случае будет представлять собой прямую линию A1B1C1F1 на рисунке 20, имеющую тот же наклон.
Как следует из расчетов и графиков, при изменении ОТ с F на D потенциалы всех точек меняются на одну и ту же величину разности потенциалов между этими точками (в данном примере на 1,05 В).
Таким образом, для получения новых величин потенциалов точек схемы после изменении ОТ, необходимо:
— либо вычесть из потенциала каждой точки полученную разность потенциалов ,
-либо перенести горизонтальную ось (ось сопротивлений) потенциальной диаграммы так, чтобы она прошла через вновь выбранную ОТ. Тогда в прежнем масштабе можно определить потенциалы других точек относительно вновь принятой ОТ.
Расчёт при смешанном соединении устройств
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.