Элементы электрической цепи постоянного тока.

Тема 1.2. Электрические цепи постоянного тока

Электрические цепи и ее элементы
Электрической цепью постоянного тока называют совокупность устройств и объектов: источников электрической энергии, преобразователей, потребителей, коммутационной, защитной и измерительной аппаратуры, соединительных проводов или линии электропередачи.

Электрические и электромагнитные процессы в этих объектах описываются с помощью понятий об электродвижущей силе (ЭДС — E ), токе ( I ) и напряжении ( U ).

Элементы цепи можно разделить на три группы:

1) элементы, предназначенные для генерирования электроэнергии (источники энергии, источники ЭДС);

2) элементы, преобразующие электроэнергию в другие виды энергии: механическую, тепловую, световую, химическую и т.д. (эти элементы называются приемниками электрической энергии или потребителями);

3) элементы, предназначенные для передачи электрической энергии от источника к приемникам (линии электропередачи, соединительные провода); элементы, обеспечивающие уровень и качество напряжения и т.д.

Источники питания цепи постоянного тока – это гальванические элементы, электрические аккумуляторы, электромеханические генераторы, термо- и фотоэлементы и др.

Электрическими приемниками или потребителями постоянного тока являются электродвигатели, преобразующие электрическую энергию в механическую, нагревательные и осветительные приборы, электролизные установки и др. Все электоприемники характеризуются электрическими параметрами, среди которых основные – напряжение и мощность. Для нормальной работы электроприемника на его зажимах необходимо поддерживать номинальное напряжение. По ГОСТ 721-77 напряжение равно 27, 110, 220, 440 В, так же 6, 12, 24, 36 В.

Коммутационная аппаратура служит для подключения потребителей к источникам, то есть для замыкания и размыкания источников электроцепи.

Защитная аппаратура предназначена для размыкания цепи в аварийных ситуациях.

Измерительная аппаратура предназначена для замера тока, напряжения и других электрических величин.

Линии электропередачи используются, когда источники и потребители удалены друг от друга на большие расстояния. Соединительные провода предназначены для соединения между собой зажимов или электродов элементов электрической цепи.

Активные и пассивные элементы

Элемент называется пассивным , если он не может вызывать протекание тока, то есть если он не создает тока или ЭДС. Если собрать несколько пассивных элементов (резисторы, конденсаторы, катушки индуктивности) в электрическую цепь, то ток в цепи не потечет.

Элемент, который создает ЭДС и вызывает протекание тока, называется активным (источники электроэнергии).

Линейные и нелинейные цепи

Электрическая цепь называется линейной , если электрическое сопротивление или другие параметры участков, не зависят от значений и направлений токов и напряжений. Электрические процессы линейной цепи описываются линейными алгебраическими и дифференциальными уравнениями.

Если электрическая цепь содержит хотя бы один нелинейный элемент , то она является нелинейной.

Топологические элементы электрической цепи.

Графическое изображение электрической цепи называется электрической схемой. Электрическая схема включает: узлы, ветви, контуры.

Ветвь – совокупность элементов, соединенных последовательно. По ветви протекает один и тот же ток.

Узел – точка соединения трех или более ветвей.

Контур – совокупность ветвей, при обходе которых осуществляется замкнутый путь.

Простейшая электроцепь имеет один контур с одной ветвью и не имеет узлов. Сложные электроцепи имеют несколько контуров.

Положительные направления тока, напряжения и ЭДС.

Чтобы правильно записать уравнения, описывающие процессы в электрических цепях, и произвести анализ этих процессов, необходимо задать условные положительные направления ЭДС источников питания, тока в элементах или ветвях цепи и напряжения на зажимах элементов цепи или между узлами цепи.

Внутри источника ЭДС постоянного тока положительным является направление ЭДС от отрицательного полюса к положительному полюсу. Это соответствует определению ЭДС как величины, характеризующей способность сторонних сил вызывать электрический ток.

По отношению к источнику ЭДС все элементы цепи составляют внешний участок цепи.

За положительное направление тока в цепи принимают направление, совпадающее с направлением ЭДС. Во внешней цепи положительным является направление от положительного полюса источника к отрицательному полюсу. В электронной теории – направление совпадает с направлением положительно заряженных частиц.

Условным положительным направлением падения напряжения (или просто напряжения) на элементах цепи или между двумя узлами цепи принимают направление, совпадающее с условно положительным направлением тока в этом элементе или в этой ветви. Положительное направление напряжения на зажимах источника ЭДС всегда противоположно положительному направлению ЭДС.

Действительные направления электрических величин, определяемые расчетом, могут совпадать или не совпадать с условными направлениями. При расчетах если определено, что ток, ЭДС и напряжения положительны, то их действительные направления совпадают с условно принятыми положительными направлениями, если отрицательны, то не совпадают.

Основные законы электрической цепи

Условное обозначение параметров в цепях постоянного и переменного тока.

i – переменный ток; I – постоянный ток;

u – переменное напряжение; U – постоянное напряжение;

e – переменная ЭДС; E – постоянная ЭДС;

Источник

Основные формулы электричества

Изучение основ электродинамики, электрики невозможно без определения электрического поля, точных зарядов, сопротивления и прочих явлений.

Формулы электричества

Поэтому важно рассмотреть все основные формулы электричества и примеры решения задач с их использованием.

Закон Кулона

Согласно короткому описанию, это физический закон, который говорит о взаимодействии между прямо стоящими точечными электрозарядами в зависимости от того, на каком расстоянии они находятся. Согласно полному определению, формулировка обозначает, что между двумя точками в виде электрических зарядов формируется вакуум. Там появляется конкретная сила, которая пропорциональна умножению их модульных частиц, поделенных на квадратный показатель расстояния.

Расстояние — длина, которая соединяет заряды. Сила взаимодействия направлена по отрезку. Кулоновская сила — сила, отталкивающая при зарядах минус-минус и плюс-плюс и притягательная при минус-плюс и плюс-минус.

Обратите внимание! Электрическая сила формула выглядит так: F=k⋅|q1|⋅|q2|/r2, где F — сила заряда, q — величина заряда, r — вектор или расстояние между зарядами, а k — коэффициент пропорциональности. Последний равен c2·10−7 Гн/м.

Закон Кулона

Решение задачи с законом Кулона. При наличии заряженных шариков, которые находятся на расстоянии 15 см и отталкиваются с силой 1 Н в поиске начального заряда, выявить неизвестное можно, переведя основные единицы в систему СИ и подставив величины в указанную формулу. Выйдет значение 2 * 5 * 10 (-8) = 10 (-7).

Напряженность поля уединенного точечного заряда

Электрическое поле будучи материей, создаваемой электрическими точечными зарядами, характеризуется разными величинами, в том числе напряженностью. Напряженность выступает векторной величиной или силовой характеристикой поля, которая направлена в сторону электростатического взаимодействия зарядов. Чтобы получить ее, нужно использовать формулу E = k (q / r (2)), где Е — векторное поле.

Напряженность поля уединенного точечного заряда

Согласно данной формулировке, напряженность поля заряда имеет обратную пропорциональность квадратному значению расстояния от заряда. То есть если промежуток увеличивается в несколько раз, показатель напряжения снижается в четыре.

Применить закон можно для решения задач. Например, неизвестен радиус. Тогда нужно преобразовать константу. Нужно решить уравнение E / r (2) = kq, подставив известные числа.

Потенциал точки в поле точечного заряда

Потенциалом в электростатическом поле называется скалярная величина, которая равна делению потенциального показателя энергии заряда на него. Он не зависит от величины q, которая помещена в область. Так как потенциальный показатель энергии зависит от того, какая выбрана система координат, то потенциал определяется с точностью до постоянной. Он равен работе поле, которое смещает единичный положительный заряд в бесконечность. Выражается через ф = W / q =const.

Вам это будет интересно Как заряжается конденсатор

Потенциал точки в поле точечного заряда

Обратите внимание! В задачах можно преобразовывать константу. Если неизвестно W, то можно поделить q на ф, а если q — то, W на ф.

Потенциальная энергия заряда в электростатическом поле

Потенциальная энергия заряда в электростатическом поле
Поскольку работа электрического поля не зависит от выбранного движения заряженной частицы, а от его начального и конечного положения, есть термин потенциальной энергии. Это скалярная величина в координате пространства, которая показывает, как работает сила, когда частица перемещается по произвольному промежутку из одной в другую точку. Она равна разности значений передвижения частиц в этом промежутке. Выражается в следующем виде: А = П1 — П2, где П1 может быть x, y и z, а П2 — x2, y2 и z2. В задачах по физике нужно рисовать график, подставлять в константу известные значения и решать уравнения.

Потенциальная энергия заряда q1 в поле точечного заряда

Во время перемещения заряженных частиц по полю из одной точки в другую они совершают некую работу за определенный временной промежуток. Потенциальная энергия в этих точках не зависит от того, какой путь держат заряженные частицы. Энергия первого заряда пропорциональна его модулю. Выражается это все в формуле, представленной на картинке ниже. Задачи решать можно, используя представленную константу и вставляя известные значения.

Потенциальная энергия заряда q1 в поле точечного заряда

Теорема Гаусса

Основной закон в электродинамике, входящий в уравнения Максвелла. Это следствие из кулоновского умозаключения и принципа суперпозиции. По ней вектор напряжения поля движется сквозь произвольное значение замкнутой поверхности, окруженной зарядами. Он имеет пропорциональность сумме заряженных частиц, которые находятся внутри этого замкнутого пространства. Указанный вектор поделен на е0. Все это выражается формулой, указанной ниже.

Теорема Гаусса

Напряженность электрического поля вблизи от поверхности проводника

Напряженность суммарного пространства заряженных частиц имеет прямую пропорциональность поверхностному показателю их плотности. Если в задаче требуется найти напряженность, а поверхностная заряженная плотность это сигма, то нужно нарисовать цилиндр и обозначить, что поток сквозь его боковую поверхность равен 0. В таком случае линии напряженности будут параллельны боковой поверхности. Получится, что ф = 2ф, осн =2еs, а 2es =q / 2ε0.

Напряженность электрического поля вблизи от поверхности проводника

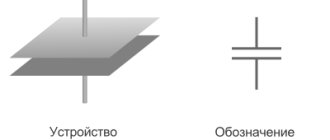
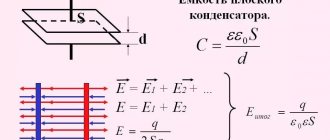
Емкость плоского конденсатора

Емкостью называется проводниковая характеристика, по которой электрический заряд может накапливать энергию. Плоским конденсатором называются несколько противоположно заряженных пластин, разделенных диэлектрическим тонким слоем. Емкостью плоского конденсатора считается его характеристика, способность к накоплению электрической энергии.

Обратите внимание! Это физическая величина, которая равна делению заряда на разность потенциалов его обкладки. Зарядом при этом служит заряженная одна пластина.

Если в задаче требуется узнать емкость конденсатора из двух пластин с площадью в 10(-2) квадратных метров и в них находится 2*10(-3) метровый лист, ε0 электрическая постоянная с 8,85×10-12 фарад на метр и ε=6 — диэлектрическая проницаемость слюды. В таком случае нужно вставить значения в формулу C= ε* ε* S/d.

Емкость плоского конденсатора

Энергия плоского конденсатора

Поскольку любая частица конденсатора имеет способность запаса энергии, который сохранен на конденсаторной обкладке, вычислить эту самую Е просто, поскольку чтобы элемент зарядился, ему нужно совершить работу. Работа совершается полем. В результате была выведена следующая формула: Еp = А = qEd, где А является работой, d — расстоянием.

Энергия

​Методы расчета электрических цепей

Чтобы верно рассчитать электроцепь, ее параметры на разных частях, применяют специальные методы, такие как:

• метод преобразования цепи;
• метод наложения;
• метод контурных токов;
• метод эквивалентного генератора;
• метод узловых потенциалов;
• метод применения законов Кирхгофа.

Метод контурных токов базируется на использовании дополнительных значений контурных токов, соответствующих закону Кирхгофа.

Метод эквивалентного генератора применяют для вычисления токов одного или нескольких разветвлений. Данный метод также называется теоремой об активном двухполюснике.

Метод узловых потенциалов дает возможность уменьшить порядок системы уравнений. Он заключается в определении потенциалов всех узлов цепи по заданным потенциалам токов всех разветвлений. В основе данного метода лежит первый закон Кирхгофа.

Самые часто применяемые методы для вычисления параметров цепи – это метод применения законов Кирхгофа и метод преобразования цепи. Рассмотрим их подробнее.

Метод преобразования электрической цепи

Этот метод состоит в том, чтобы верно рассчитать распределение токов в цепи. Подключенные последовательно или параллельно сопротивления заменяют на одно сопротивление, в результате чего распределение тока не изменяется.

В случае последовательного соединения сопротивлений они будут подключены так, что конец предыдущего будет соединяться с началом последующего. При таком соединении сила тока будет иметь одинаковую величину в каждом резисторе.

В любой электроцепи есть источники и приемники электроэнергии, что соединены проводами. Такое соединение делает возможным движение тока по проводам от одного элемента к другому. Источники бывают источниками напряжения и тока.

Идеальным источником напряжения считается такой, напряжение на клеммах которого не меняется во времени, не зависимо от силы тока, который он выдает в нагрузку, а его внутреннее сопротивление приравнивается к нулю.

Идеальным источником тока считается такой, который выдает постоянное во времени значение силы тока, не зависящее от напряжения на клеммах, а его внутреннее сопротивление приравнивается к бесконечно большой величине.

Источник



ПОСТОЯННЫЙ ТОК

Электрический ток — это упорядоченное движение заряженных частиц (электронов и ионов). За направление тока условно принято направление движения положительных зарядов, т.е. от « + » к « — ».

Условия, необходимые для существования электрического тока:

• Наличие свободных заряженных частиц;
• Наличие электрического поля, действующего на заряженные частицы с силой в определённом направлении;
• Наличие замкнутой электрической цепи.

Действия тока:

1. Тепловое: проводник по которому течет ток нагревается.
2. Химическое: электрический ток может изменять химический состав проводника (электролита).
3. Магнитное: ток оказывает силовое воздействие на соседние токи и намагниченные тела. Вокруг проводника с током существует магнитное поле.

Электродвижущая сила.

Если два заряженных тела соединить проводником, то через него пойдет кратковременный ток. Избыточные электроны с отрицательно заряженного тела перейдут на положительно заряженное. Потенциалы тел окажутся одинаковыми, значит, напряжение на концах проводника станет равно нулю, и ток прекратится. Для существования длительного тока в проводнике нужно поддерживать разность потенциалов на его концах неизменной. Этого можно достичь, перенося свободные электроны с положительного тела на отрицательное так, чтобы заряды тел не менялись со временем.

Силы электрического взаимодействия сами по себе не способны осуществлять подобное разделение зарядов. Они вызывают притяжение электронов к положительному телу и отталкивание от отрицательного. Поэтому внутри источника тока должны действовать сторонние силы, имеющие неэлектрическую природу и обеспечивающие разделение электрических зарядов.

Сторонние силы — любые силы, действующие на электрические заряженные частицы, за исключение сил, электростатического происхождения (т.е. кулоновских).

ЭДС – электродвижущая сила – физическая величина, определяемая работой , совершаемой сторонними силами при перемещении единичного положительного заряда от «+» полюса к «-» полюсу внутри источника тока. Является энергетической характеристикой источника тока.

Основные характеристики электрического тока

Виды соединений источников тока

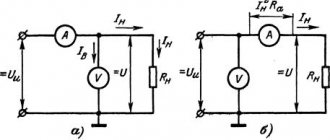
Шунтирование амперметра.

Важным примером применения последовательного и параллельного соединения проводов являются различные схемы включения электроизмерительных приборов. Допустим, что имеется некоторый амперметр, рассчитанный на максимальный ток Imax, а требуется измерить большую силу тока. В этом случае параллельно к амперметру присоединяют малое сопротивление r, по которому направится большая часть тока. Его называют обычно шунтом. Сопротивление амперметра – R, и пусть R/r=n. Сила тока в цепи, амперметре и в шунте равны соответственно I, Iа и Iш

Параллельное присоединение шунта к измерительному прибору с целью изменения его чувствительности называют шунтированием. Схема шунтирования амперметра добавочным малым сопротивлением r.

Постоянный ток. Работа и мощность. Закон Джоуля – Ленца.

Работа электрического поля по перемещению заряда ∆ q из одной точки в другую равна произведению напряжения U между этими точками на величину заряда Dq: A=DqU

РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛОВ И ТОКА В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ

Для того чтобы разобраться в прохождении тока по электриче­ским цепям, надо представить, как распределяются в ней электриче­ские потенциалы. Электрический ток проходит всегда от точек цепи, находящихся под большим потенциалом, к точкам, находящимся под меньшим потенциалом. Если какая-либо точка цепи соединена с зем­лей, то потенциал ее принимается равным нулю; в этом случае потенциалы других точек цепи будут равны напряжениям, действующим между этими точками и землей.

Рассмотрим этот вопрос на нескольких конкретных примерах. На рис. 27,
а
показано распределение потенциалов в последовательной электрической цепи, находящейся под напряжением, при условии, что
r1 = r2 = r3.
Точка
А
имеет наибольший положительный потенциал φА, так как она соединена с положительным полюсом источника (сам источник на схеме отсутствует — показаны лишь провода сети, соединяющей его с точками
А
и
Г).
Потенциал
φБ
в точке
Б
будет меньше, чем в точке
А,
следовательно, на участке
А Б
ток идет от точки
А
к точке
Б.
Разность потенциалов между точками
А
и
Б
рав­на падению напряжения
U1 = Ir1в резисторе с сопротивлением r1.
Это падение напряжения возрастает постепенно по мере перехода от точки
А
к точке
Б,
поэтому вдоль резистора с сопротивлением r
1
потенциал также уменьшается постепенно. В точке
В
потенциал равен нулю. Разность потенциалов между точками
Б
и
В
равна падению на­пряжения
U2 = Ir2 в
резисторе с сопротивлением
r2.
Точка
Г
будет иметь отрицательный потенциал по отношению к точке
В
(она соеди­нена с отрицательным полюсом источника), поэтому ток I идет от точ­ки
В
к точке
Г.
Следует отметить, что при заземлении одной точки элек­трической цепи распределение токов в ней не изменяется, так как при этом не образуется никаких новых ветвей, по которым могли бы проте­кать токи. Если заземлить две или большее число точек цепи, имеющих разные потенциалы, то через землю образуются дополнительные токопроводящие ветви и распределение тока в цепи меняется.

Последовательное и параллельное соединение проводников

Последовательное и параллельное соединение проводников это основные виды соединения проводников, встречающиеся на практике. Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.

Рассмотрим два типичных случая. Первый из них это когда два или боле проводников обладающих сопротивлением включены последовательно. Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.

Рисунок 1 — последовательное соединение проводников

Падение напряжения на сопротивлениях можно определить исходя из закона Ома.

Формула 1 — Падение напряжения на сопротивлении

Сумма этих напряжений будет равна полному напряжению, приложенному к цепи. Напряжение на проводниках будет распределяться пропорционально их сопротивлению. То есть можно записать.

Формула 2 — соотношение между сопротивлением и напряжением

Суммарное же сопротивление цепи будет равно сумме всех сопротивлений включенных последовательно.

Формула 3 — вычисление суммарного сопротивления при параллельном включении

Второй случай, когда сопротивления в цепи включены параллельно друг другу. То есть в цепи есть два узла и все проводники обладающие сопротивлением подключаются к этим узлам. В такой цепи токи во всех ветвях в общем случае не равны друг другу. Но сумма всех токов в цепи после разветвления будет равна току до разветвления.

Рисунок 2 — Параллельное соединение проводников

Формула 4 — соотношение между токами в параллельных ветвях

Сила тока в каждой из разветвлённой цепи также подчиняется закону Ома. Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.

Формула 5 — Распределение токов в параллельных ветвях

Чтобы найти полное сопротивление цепи в этом случае необходимо сложить величины обратные сопротивлениям то есть проводимости.

Формула 6 — Сопротивление параллельно включённых проводников

Также существует упрощённая формула для частного случая когда параллельно включены два одинаковых сопротивления.

Формула 7 — сопротивление двух одинаковых проводников

При параллельном включении сопротивлений говорят, что общее сопротивление получается меньше наименьшего. В общем случае цепь может состоять из смешанно соединённых проводников. Тогда ее разбивают на участки, где они соединены либо параллельно, либо последовательно и производят расчет.

Рисунок 3 — смешанное соединение проводников

Если цепь нельзя разбить на элементарные участки токи в ней рассчитывают с помощью законов Киргкофа.

Рисунок 4 — цепь, рассчитываемая с помощью правил Киргкофа

Схемы Электрических Цепей Постоянного Тока

При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС или напряжения, сопротивления элементов электрической цепи, и задача сводится к определению токов в ветвях цепи. Таким образом, электрическая цепь на рис.

Точка Н определяет номинальный режим, если напряжение и ток соответствуют их номинальным значениям Uном и Iном, приведенным в паспорте источника электрической энергии.

Элемент электрической цепи, параметры которого сопротивление и др. Электрические цепи (часть 1)

Элементы цепи Электрическая цепь содержит в себе такие составляющие, как источники энергии, потребители, а также соединяющие их провода. По закону Ома токи в каждой ветви: По первому закону Кирхгофа общий ток Смешанное соединение — комбинация первых двух соединений, где параллельное соединение может быть преобразовано к последовательному.

Для их составления необходимо задать условные направления токов в ветвях номер введем в соответствии с порядковым номером сопротивлений.

Метод узловых потенциалов Вторым методом, которым пользуются для решения сложных цепей, является метод узловых потенциалов. Тогда из выражения 1.

Внешняя вольт-амперная характеристика источника электрической энергии Точка X вольт-амперной характеристики источника электрической энергии отвечает режиму холостого хода х.

Подключение цепи к источнику постоянной ЭДС 5. Существуют дополнительные приборы цепи, например, выключатели, измерители тока и защитные аппараты. КОНДЕНСАТОР В ЦЕПИ ПОСТОЯННОГО И ПЕРЕМЕННОГО ТОКА [РадиолюбительTV 89]

Расчет цепей методом эквивалентных преобразований

При расчете электрических цепей постоянного тока, как правило, известны параметры источников электрической энергии и параметры остальных элементов электрической цени. Задача сводится к определению токов во всех ветвях цепи и напряжений на всех ее элементах.

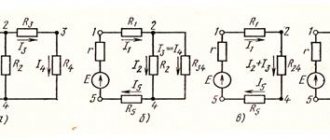
При расчете электрических цепей часто возникает возможность преобразования схем этих цепей в более простые и удобные для расчета. Одними из наиболее часто применяемых на практике методов эквивалентных преобразований является преобразование схемы со смешанным соединением элементов и взаимные преобразования соединений треугольник и звезда.

Смешанное соединение представляет собой сочетание ранее рассмотренных более простых соединений последовательного и параллельного. На рис. 1.22 показан пример схемы со смешанным соединением. Она легко приводится к одноконтурной цени. Вначале вычисляется эквивалентное сопротивление

параллельно соединенных сопротивлений и

или

Из

получаем

Полученные выражения называют «правилом плеч». Они позволяют разбить ток

на два параллельных тока и .

В результате выполненных преобразований получаем схему с двумя последовательно соединенными сопротивлениями

и (рис. 1.22,6). Суммируем эти сопротивления и получаем одноконтурную схему (рис. 1.22,в) с сопротивлением , эквивалентным смешанному соединению сопротивлений и .

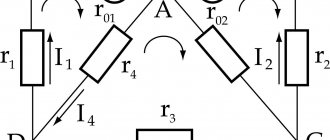
Преобразование треугольника в звезду рассмотрим на примере мостовой схемы, изображенной на рис. 1.23,а. Схема содержит четыре плеча

и . В измерительной технике к одной из диагоналей подключается источник (между узлами 1 и 3), а во вторую диагональ (между узлами 4 и 2) включается измерительный прибор. В рассматриваемой схеме в эту диагональ включено сопротивление .

Пусть

. Требуется вычислить сопротивление мостовой схемы между точками и .

Цепь не содержит последовательных или параллельных соединений элементов, но имеет два пассивных треугольника, образованных сопротивлениями

и четыре звезды, центрами схождения лучей которых являются узлы 1, 2, 3, 4. Рассмотрим порядок расчета сопротивления мостовой схемы между узлами 1 и 3 при использовании преобразования треугольник — звезда.

Вначале треугольник сопротивлений

заменим эквивалентной звездой (рис. 1.23,6). В соответствии с (1.9) сопротивление

Аналогично вычислим сопротивления

и . Получим .

В результате выполненных преобразований получим схему, изображенную на рис. 1.23(6). Заменив последовательно соединенные сопротивления

и эквивалентными сопротивлениями и , получим эквивалентную схему, изображенную на рис.1.23,в. Сопротивление . Сопротивление .

Из эквивалентной схемы на рис. 1.23,в вычислим сопротивление мостовой схемы между точками

и

Для проверки вычислений выполнен с помощью программы схемотехнического моделирования MicroCap анализ по постоянному току схемы, изображенной на рис. 1.23,д. Из приведенных на рис. 1.24 результатов анализа видно, что при подключении мостовой схемы к источнику постоянной ЭДС

через схему протекает ток, равный 1 А. Отсюда следует что сопротивление моста между точками и равно 10 Ом, что и подтверждает результаты расчета.

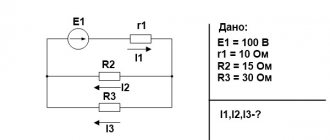
Эта теория взята со страницы помощи с заданиями по электротехнике:

Помощь по электротехнике

Возможно эти страницы вам будут полезны:

Основные законы электрических цепей

Эквивалентные преобразования пассивных участков электрической цепи

Методы расчета сложных электрических цепей

Потенциальная диаграмма в цепях постоянного тока

Электрическая цепь постоянного тока

Алгебраическая сумма падений напряжений на резистивных элементах в любом замкнутом контуре равно алгебраической сумме ЭДС. Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.

Источник электрической энергии характеризуется понятием ЭДС Е , под которой понимают величину, численно равную энергии, получаемой внутри источника единицей электрического заряда.

При расчете в схеме электрической цепи выделяют несколько основных элементов. Этот метод основан на составлении уравнений по первому закону Кирхгофа: Схема сложной электрической цепи с двумя узлами.

Для разных электротехнических устройств указывают свои номинальные параметры.

Электрическая цепь в режиме короткого замыкания имеет сопротивление, которое равно нулю. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.

Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников.

В случае последовательного соединения сопротивлений в ветви В общем виде уравнения узловых потенциалов имеют вид: Если в схеме имеются источники тока, то слагаемое в правой части будет равно сумме источников тока: Метод узловых потенциалов имеет преимущество, если число независимых узлов меньше числа контуров. Желательно во всех контурах положительные направления обхода выбирать одинаковыми, например, по часовой стрелке, как показано на рис. Устройство и принцип работы двигателя постоянного тока. Схема двигателя постоянного тока.

Формулы для постоянного электрического тока

Постоянный электрический ток не изменяется в величине и направлении. Он используется для расчета замкнутой, однородной цепи, мощности и прочих параметров. Поэтому важно знать формулы для него и основные законы, связанные с ним.

Вам это будет интересно Особенности напряжения прикосновения

Основной список формул

Закон Ома для участка однородной цепи

Чтобы электрический ток существовал, нужно поле. Для его образования, нужны потенциалы или разность их, выраженная напряжением. Ток будет направлен на снижение потенциалов, а электроны начнут свое передвижение в обратном направлении. В 1826 г. Г. Ом провел исследование и сделал заключение: чем больше показатель напряжения, тем больше ток, который проходит через участок.

К сведению! Смежные проводники при этом проводят электричество по-разному. То есть каждый элемент имеет свою проводимость, электрическое сопротивление.

В результате, согласно теореме Ома, сила тока для участка однородной цепи будет иметь прямую пропорциональность показателю напряжения на нем и обратную пропорциональность проводниковому сопротивлению.

Закон Ома

По формуле I = U / R, где I считается силой тока, U — напряжением, а R — электрическим сопротивлением, последнее значение можно найти, если p * l / S, где p является удельным проводниковым сопротивлением, l — длиной проводника, а S — площадью поперечного проводникового сечения.

Закон Ома для замкнутой цепи с источником тока

Ом сделал формулу и для замкнутой цепи. По ней ток на этом участке из токового источника, имеющего внутреннее и внешнее нагрузочное сопротивление, равен делению электродвижущей силы источника на сумму внутреннего и внешнего сопротивления. Она выглядит так: I = e / R + r, где I является токовой силой, е — ЭДС, R — сопротивлением, а r — внутренней сопротивляемостью источника напряжения.

Обратите внимание! В физическом смысле по этому закону, чем выше показатель ЭДС, тем выше источник энергии, больше скорость движения зарядов. Чем выше сопротивляемость, тем ниже величина тока.

Закон Ома для замкнутой цепи

Работа постоянного тока

Энергия, когда проходит через проводник, упорядоченно двигается в носитель. Во время движения она совершает работу. В результате работой постоянного тока называется деятельность поля, направленная на перенос электрических зарядов по проводнику. Она равна умножению I на совершаемое работой напряжение и время.

Закон Джоуля-Ленца

Когда электричество проходит через какой-то проводник с сопротивляемостью, всегда высвобождается теплота. Количество тепла, которое высвободилось за определенный промежуток времени, определяет закон Джоуля-Ленца. По формуле мощность тепла равняется умножению плотности электричества на напряжение — w =j * E = oE(2).

Обратите внимание! В практическом понимании закон имеет значение для снижения потери электроэнергии, выбора проводника для электроцепи, подбора электронагревательного прибора и использования плавкого предохранителя для защиты сети.

Закон Джоуля-Ленца

Полная мощность, развиваемая источником тока

Мощность — работа, которая совершается за одну секунду времени. Электрическая мощность является физической величиной, которая характеризует скорость передачи с преобразованием электроэнергии.

Работа, которая развивается источником электроэнергии по всей цепи, это полная мощность. Ее можно определить по формуле Р = El, где E считается ЭДС, а I — величиной токовой характеристики.

К сведению! Если есть линейная нагрузка, то полный мощностный показатель равен квадратному корню из квадратов активной и реактивной работы источника. Если есть нелинейная нагрузка, то она равна квадратному корню из квадратов активной и неактивной работы источника.

Полная мощность

В практических измерениях такая работа выражается в киловаттах в час. Используется, чтобы измерять потребление электричества в бытовых и производственных условиях, определять выработанную электрическую энергию в электрическом оборудовании.

Полезная мощность

Максимальная или полезная мощность — та, что выделяется во внешнем промежутке цепи, то есть во время нагрузки резистора. Она может быть применена для выполнения каких-либо задач. Подобное понятие можно применить, чтобы рассчитать, как работает электрический двигатель или трансформатор, который способен на потребление активной и реактивной составляющей.

Вам это будет интересно Описание кабеля КСПВ

Полезная мощность

Полезный мощностный показатель можно рассчитать по трем формулам: P = I 2R, P = U2 / r, P = IU, где I является силой тока на определенном участке цепи; U — напряжением на части клемм (зажимов) токового источника, а R — сопротивлением нагрузки или внешней цепью.

Коэффициент полезного действия источника тока

Коэффициентом полезного действия токового источника называется деление полезного мощностного показателя на полный. Если внутреннее сопротивление источника равно внешнему, то половина результатов всей работы будет утеряна в источнике, а другая половина будет выделена на нагрузке. В такой ситуации КПД будет равен 50 %.

Если рассматривать это понятие наиболее полно, то когда электрические заряды перемещаются по замкнутой электрической цепи, источник тока выполняет определенную полезную и полную работу. Совершая первую, он перемещает заряды во внешнюю цепь. Делая вторую работу, заряженные частицы перемещаются по всему участку.

КПД источника тока

Обратите внимание! Полезное действие достигается, когда сопротивление внешней электроцепи будет иметь определенное значение, зависящее от источника и нагрузки. Соотношения полезной работы на полную выражают формулой: η = Аполез / Аполн = Рполез / Рполн = U/ε = R / (R + r).

Первое правило Кирхгофа

Согласно первому закону Кирхгофу, токовая сумма в любом участке электрической цепи равняется нулевому значению. Направленный заряд к узлу положительный, а от него — отрицательный. Алгебраическая токовая сумма зарядов, которые направлены к узлу, равна сумме тех, которые направлены от него. Если перевести это правило, то можно получить следующее определение: сколько тока попадает в узел, столько и выходит из него. Это правило вытекает из закона о сохранности заряженных частиц.

Благодаря решению линейных уравнений на основе кирхгофских правил можно отыскать все токовые значения и напряжения на участках постоянного, переменного и квазистационарного электротоков.

Обратите внимание! В электотехнике правило Кирхгофа имеет особое значение, поскольку оно универсально для решения многих поставленных задач в теории электроцепи. С помощью него можно рассчитать сложные электрические цепи. Применяя его, можно получить систему линейных уравнений относительно токам или напряжениям на всех межузловых ветвях цепей.

Первое правило Кирхгофа

Второе правило Кирхгофа

Второе кирхгофское правило вытекает из первого и третьего максвеллского уравнения. По нему алгебраическая сумма напряжений на резистивных элементах замкнутого участка равна сумме ЭДС, которая входит в него. Если на участке нет ЭДС, то суммарный показатель падения напряжения равен нулевому значению. Если еще проще, то во время полного обхода контура потенциал изменяется. Он возвращается на исходное значение.

Частый случай для участка одного контура — это закон Ома. Составляя уравнения напряжений для контура, требуется подобрать его положительный обход. Чтобы это сделать, нужно знать, что при подборе обхода показатель падения напряжения ветви будет положительным, если обходное направление в ветви совпадает с тем, которое было ранее выбрано. Если оно не совпадает, то показатель напряжения ветви будет отрицательным.

Важно! Второе правило Кирхгофа можно использовать в линейной или нелинейной линеаризованной цепи при любом изменении токов и напряжения.

Второе правило Кирхгофа

В результате, чтобы понять основы физики явлений, электрики, электродинамики и с успехом использовать знания в процессе жизнедеятельности, необходимо знать выведенные теоремы, законы, формулы и правила в области электричества, которые представлены выше. Например, представляя, как выглядит та или иная формула, можно решить любую задачу в учебнике по физике или жизни.

Элементы цепи

При сравнении внешних характеристик источника ЭДС рис. Мощность трёхфазной цепи 3.

Классический метод расчёта переходных процессов 5. В зависимости от электропроводности все вещества подразделяют на: 1.

Последовательное соединение в цепи Большое количество электрических цепей состоят из нескольких приемников тока.

Согласованный режим Согласованный режим электрической цепи обеспечивает максимальную передачу активной мощности от источника питания к потребителю. На схеме этот элемент выглядит следующим образом. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.