Приведение вторичной обмотки к первичной
Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если у первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков.
Представим себе, что реальная вторичная обмотка трансформатора с числом витков w2 заменена воображаемой, или приведенной, обмоткой с числом витков w2’ = w1. При этом число витков вторичной обмотки изменится в
раз. Величина k называется коэффициентом приведения или коэффициентом трансформации. Более подробно о том, что называется коэффициентом трансформации и как определить коэффициент трансформации изложено в статье «Принцип действия и виды трансформаторов».
В результате такой замены, или приведения, электродвижущая сила E2’ и напряжение U2’ приведенной обмотки также изменяются в k раз по сравнению с величинами E2 и U2 реальной вторичной обмотки:
| (1) | |
| (2) |
Чтобы мощности приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство
где I2’ – приведенный вторичный ток. Отсюда с учетом второго равенства (2) следует, что
| (3) |
Намагничивающие силы приведенной и реальной обмоток на основании выражений (1) и (3) равны:
| (4) |
Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого, кроме соблюдения условия (4), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне магнитопровода трансформатора так же, как и реальная вторичная обмотка (смотрите например, рисунок 1, в статье «Магнитопроводы трансформаторов» и рисунок 1, в статье «Элементы конструкции и способы охлаждения масляных трансформаторов»). Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в k раз. Но поскольку приведенная обмотка имеет в k раз больше витков, то в итоге активное сопротивление приведенной обмотки в k2 раз больше, чем реальной:
Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки x2’ и реальной x2 существует такое же соотношение:
Очевидно, что потери в приведенной и реальной обмотках одинаковы:
Одинаковы также относительные падения напряжения во вторичных обмотках приведенного и реального трансформаторов:
Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.
| (5) | |
| (6) |
Конструкция и принцип действия
Конструкция трансформатора предусматривает наличие следующих составных частей:
- сердечника,
- первичной и вторичной обмоток.
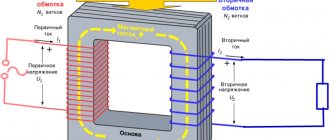
Принцип работы трансформатора
В зависимости от особенностей конструктивного устройства, работу трансформаторов обеспечивает наличие автоматических блоков, управляющих агрегатом, коммутационных узлов для подключения питания, масляных ёмкостей для охлаждения и пр.
При подаче напряжения на первичную катушку, образуется магнитное поле и возникает электродвижущая сила (ЭЛС), наводящая напряжение на вторичном контуре. Трансформация характеристик напряжения и тока достигается путём разного количества витков на входном и выходном контурах. У приведённого трансформатора число витков на входе и выходе условно принято равным, что обеспечивает указанное выше значение коэффициента трансформации, при сохранении количества фаз и других характеристик сети без изменения.
Параметры схемы замещения
Рассмотрим параметры схем замещения рисунка 1 при k = w1 / w2 [смотрите равенство (1)]. Приведенная взаимная индуктивность на основании равенств (6) и (10), в представленных статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и равенства (19), настоящей статьи
или на основании выражения (4), в представленного в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние»
| (20) |
Последний член выражения (20) весьма мал по сравнению с первым, и поэтому с достаточной точностью
| M12’ ≈ Lс1 . | (21) |
Соответственно, согласно выражению (3), представленного в статье «Уравнения напряжений трансформатора» и выражениям (11), (19), (21), настоящей статьи,
x12’ = k × x12 = ω × k × M = ω × M12’ ≈ ω × Lс1
или
| x12’ ≈ xс1 = ω × w12 / Rµc . | (22) |
Следовательно, сопротивление x12’ с большой точностью равно сопротивлению самоиндукции первичной обмотки от потока, замыкающегося по магнитопроводу.
Ветви 1 – 2 схем замещения рисунка 1 называются намагничивающими ветвями. Протекающий по этим ветвям намагничивающий ток
| создает результирующую намагничивающую силу обмоток трансформатора Fрез = w1 × (I1 + I2’) = w1 × I1 + w1 × I2’ = F1 + F2 , которая в свою очередь создает результирующий поток стержня с амплитудой Фс. Напряжение на этих ветвях в соответствии с выражением (22), настоящей статьи и выражением (3), представленным в статье «Принцип действия и виды трансформаторов» то есть равно по значению и обратно по знаку электродвижущей силе E1, которая индуктируется в первичной обмотке результирующим потоком магнитопровода, или основным потоком трансформатора, и отстает от него на 90°. Индуктивность рассеяния первичной обмотки, согласно выражениям (9) и (10), представленных в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и выражению (17), данной статьи, S1 = L11 – k × M = Lc1 + Lв1 – k × Mc – k × Mв . Но на основании уравнений (4) и (6), представленных в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» Поэтому
Аналогично, согласно выражениям (9) и (10), представленных в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и выражению (18), данной статьи Но основании уравнений (5) и (6), представленных в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и поэтому
Таким образом, индуктивности рассеяния S1, S2 и S2’ и индуктивные сопротивления рассеяния при k = w1 / w2 определяются магнитными потоками, замыкающимися главным образом по воздуху. Однако вторыми членами равенств (23) и (24) по сравнению с первыми пренебречь нельзя, и поэтому потоки, замыкающиеся по воздуху, можно назвать потоками рассеяния лишь условно.
|
Схема замещения с учетом магнитных потерь
Потери в стали магнитопровода pмг при заданной частоте пропорциональны следующим величинам:
pмг ∼ Bc2 ∼ Фc2 ∼ E12 .
Таким образом, потери pмг пропорциональны квадрату напряжения U12 на зажимах 1 – 2 намагничивающей цепи схемы замещения рисунка 1, а. Если к этим зажимам параллельно x12’ = xc1 подключить активное сопротивление rмг, как показано на рисунке 2, а, то потери в этом сопротивлении также будут пропорциональны U12. Значение сопротивления rмг можно подобрать так, чтобы потери в нем равнялись магнитным потерям:
pмг = m1 × U122 / rмг = m1 × E12 / rмг .
Отсюда
| rмг = m1 × E12 / pмг . | (26) |
Рисунок 2. Намагничивающая цепь схемы замещения с учетом магнитных потерь
Величину pмг при заданной электродвижущей силе E1 можно считать известной из расчетных (смотрите статью «Расчет магнитной цепи трансформатора») или опытных данных. Тогда можно считать известным также rмг.
Намагничивающий ток
разделяется в двух ветвях намагничивающей цепи (рисунок 2, а) на активную Iмa и реактивную Iмr составляющие (смотрите статью «Расчет магнитной цепи трансформатора»), из, из которых первая определяет мощность магнитных потерь, а вторая создает поток магнитопровода.
Схема с двумя параллельными ветвями намагничивающей цепи хорошо согласуется с реальными физическими явлениями. Однако расчеты на основе схемы замещения вести удобнее, если объединить две параллельные ветви схемы 2, а в одну общую ветвь, как показано на рисунке 2, б. Тогда сопротивление этой ветви
| (27) |
Так как rмг >> x12’, то
| (28) |
При увеличении насыщения магнитопровода, то есть при увеличении Фс, E1 или U1, сопротивление x12’ при f = const уменьшается. Однако при этом rмг ≈ const, а значение rм уменьшается.
Схема замещения трансформатора с учетом магнитных потерь согласно рисунку 2, б показана на рисунке 3, а. Если использовать обозначения
| Z1 = r1 + jx1 ; Z2’ = r2’ + jx2’ ; Zм = rм + jxм , | (29) |
| Рисунок 3. Схема замещения двухобмоточного трансформатора с учетом магнитных потерь |
то схему замещения можно изобразить более компактно, как показано на рисунке 3, б. В режиме холостого хода I2’ = 0 и I1 = Iм – току холостого хода трансформатора.
В итоге получилась весьма простая Т-образная схема замещения трансформатора, представляющая собой пассивный четырехполюсник. Сопротивление намагничивающей цепи этой схемы Zм отражает явления в ферромагнитном магнитопроводе. Оно значительно больше сопротивлений Z1 и Z2’, которые включают в себя активные сопротивления и индуктивные сопротивления рассеяния обмоток. Для силовых трансформаторов в относительных единицах
zм* = 25 – 200 ; z1* ≈ z2*’ = 0,025 – 0,10 .
Уравнения напряжений и схему замещения трансформатора можно представлять также в относительных единицах. Имея в виду, что
Uн = zн × Iн ,
левые части уравнений вида (15) можно разделить на Uн, а правые части – на Zн × Iн, в результате чего и будет совершен переход к относительным единицам. Абсолютные значения U, I, r, x и Z в схемах замещения также можно заменить относительными. При этом расчеты режимов работы трансформатора можно вести в относительных единицах.
Нетрудно видеть, что относительные значения сопротивлений, токов и напряжений вторичной цепи будут зависеть от того, какая величина коэффициента k была использована при приведении вторичной обмотки к первичной. Неопределенность в этом вопросе исчезает, если определять k всегда одинаковым образом. Например, в силовых трансформаторах всегда берут k = w1 / w2.
Основные уравнения трансформатора. Приведённый трансформатор и схема замещения.
Схема замещения трансформатора представляет собой эквивалентную электрическую схему, которая отражает основные электромагнитные явления, происходящие в трансформаторе. Схему замещения составляют на основе уравнений трансформатора (2.15) и (2.18).
Будем учитывать потери в цепи намагничивания параметрами
тогда:
или
Полагаем при этом, что ток холостого хода Ī0 равен по модулю действующему значению тока холостого хода, а мощность
равна мощности трансформатора в режиме холостого хода. С учетом этого можно решить систему основных уравнений трансформатора относительно тока Ī1 :
Уравнению (2.20) соответствует четырехполюсник — эквивалентная электрическая схема замещения, представленная на рис. 2.11.
Рис. 2.11. Эквивалентная электрическая схема замещения
Схема замещения включает в себя параметры первичной обмотки R1
и
X1
приведенные параметры вторичной обмотки
R΄2
и
Х΄2
и параметры намагничивающего контура
Rm
и
Хm
. На вход четырехполюсника подается напряжение Ū1, к его выходу подключено приведенное значение нагрузки
Z΄H
— По первичной обмотке проходит ток Ī1 по вторичной — ток
Ī2
, по намагничивающему контуру — ток
Ī0
.
В соответствии с законом Кирхгофа сумма токов, сходящихся в узлах а или б, равна нулю: . По схеме замещения могут быть определены величины токов, мощность, мощность потерь и т. д.
Следует, однако, помнить, что параметры схемы замещения можно считать неизменными при изменении напряжения на первичной обмотке в пределах 10% от номинального значения. При дальнейшем увеличении напряжения происходит насыщение стали магнитопровода, уменьшается величина Хm
и растет намагничивающий ток.
Параметры схемы замещениямогут быть определены по результатам опытов холостого хода и короткого замыкания трансформатора.
Опыт холостого хода сводится к измерению первичного напряжения, тока и мощности первичной обмотки при разомкнутой вторичной обмотке (рис. 2.12,б).
Рис. 2.12. Опыт холостого хода (а) и схема замещения трансформатора в этом режиме (б)
При помощи регулятора напряжения РН устанавливают на первичной обмотке напряжение U0
, равное номинальному значению. Измеряют мощность
Р0
, потребляемую первичной обмоткой и ток холостого хода
I0
.
Опыту холостого хода трансформатора соответствует схема замещения (рис. 2.12,6)
Поскольку ток холостого хода Ī0
мал по сравнению с номинальным током трансформатора
Ī1
, то электрическими потерями в обмотках, которые зависят от квадрата тока, пренебрегают и считают, что вся мощность, потребляемая трансформатором в режиме холостого хода, расходуется на компенсацию магнитных потерь в стали:
. (2.21)
По измеренной мощности Р0 и току I0 можно по формуле (2.21) определить активное сопротивление намагничивающего контура Rm
:
. (2.22)
Далее, поскольку поток рассеяния во много раз меньше основного потока, то полагают, что Х1 + Хm ≈ Хm
, поэтому полное сопротивление намагничивающего контура:
Zm = U10 /I0,
(2.23)
а его индуктивное сопротивление:
(2.24)
Измерив напряжения Ul0
и
U20
первичной и вторичной обмоток, можно определить коэффициент трансформации:
k = U10 /U20
(2.25)
Опыт короткого замыкания (рис. 2.13,a) заключается в том, что вторичную обмотку трансформатора замыкают через амперметр накоротко (сопротивление ZH
=0), а к первичной посредством регулятора напряжения РН подводят такое пониженное напряжение, чтобы токи первичной и вторичной обмоток были равны номинальным значениям
I1н
и
I2н
. Это напряжение называют напряжением короткого замыкания и обозначают UK.
Напряжение короткого замыкания UK
мощных силовых трансформаторах обычно составляет 5… 15% от номинального, трансформаторов малой мощности — 25…50%.
| |
Рис. 2.13. Опыт короткого замыкания (а) и схема замещения (б)
Следует различать короткое замыкание в эксплуатационных условиях и опыт короткого замыкания. Первое представляет собой аварийное состояние трансформатора: в обмотках возникают недопустимо большие токи, внутри трансформатора выделяется большое количество тепла, что может вызвать его разрушение.
Опыт короткого замыкания служит для определения важнейших параметров трансформатора: внутреннего падения напряжения, потерь в проводниках и т. п.
Электродвижущая сила Е2K
, индуктируемая во вторичной обмотке при опыте короткого замыкания, должна быть равна падению напряжения вторичной обмотки, т.е.
E2K = I2Z2
поскольку
U2
= 0. Следовательно, при опыте короткого замыкания
Е2К
составляет лишь несколько процентов от
Е2
(2…5%). Прямо пропорционально ЭДС
Е2К
уменьшается поток в сердечнике, а вместе с ним и намагничивающий ток, возбуждающий его.
В то же время при опыте короткого замыкания потери в проводниках обмоток такие же, как и при номинальном режиме нагрузки, а потери в сердечнике пренебрежимо малы, так как они пропорциональны (приближенно) потоку.
Поэтому можно считать, что при опыте короткого замыкания вся мощность Р1K затрачивается на электрические потери в проводниках обмоток трансформатора. Поскольку током намагничивания в этом режиме можно пренебречь, то Ī1 = Ī΄2.
Положив X = X1+X̄΄2 ≈ 0, a R = R1 + R2
, получим для мощности
Р1K
(2.26)
С увеличением номинальной полной мощности SH трансформатора активная мощность РKH
, затрачиваемая во время опыта короткого замыкания при номинальном токе, относительно убывает. Например, при номинальной полной мощности SH = 5…20 кВА отношение
РKH / SH
= 3,7…3%, а при
SH
= 320…5600 кВА это отношение будет равно
PKH / SH
= 2…1%. Это означает, что чем больше мощность трансформатора, тем меньше электрические потери в его обмотках и тем выше его КПД.
На основании (2.26) определяется активное сопротивление упрощенной эквивалентной схемы трансформатора:
, (2.27)
которое называют активным сопротивлением короткого замыкания трансформатора. Это значение, определенное непосредственно из результатов опыта короткого замыкания, только ориентировочно определяет величину активного сопротивления RK нагруженного трансформатора. Чтобы обеспечить минимальные размеры трансформатора, обычно выбирают плотность тока в проводниках и индукцию в сердечниках такой величины, которым при работе соответствуют предельно допустимые температуры нагревания. Нагрев существенно изменяет активное сопротивление проводников обмоток трансформатора и потери в них. Поэтому для определения потерь в обмотках при нагрузке значение RK, найденное из опыта короткого замыкания, должно быть приведено к температуре 75 °С.
Как было показано выше, поток, замыкающийся по магнитопроводу, зависит от напряжения, приложенного к первичной обмотке трансформатора, а магнитные потери в стали пропорциональны квадрату индукции или квадрату магнитного потока. Поэтому, ввиду малости UK, магнитными потерями в стали и током холостого хода можно пренебречь. Следовательно, можно считать, что Rm ≈ 0 и Хт ≈ 0. Тогда схема замещения принимает вид, представленный на рис. 2.13,б.
Параметры схемы замещения:
ZK = Z1+ Z΄2=UK / I1H.
R1+ R΄2 = RK = P1K / I2H, (2.28)
Треугольник, образуемый векторами падений напряжений на полном, индуктивном и активном сопротивлениях короткого замыкания называют характеристическим треугольником или треугольником короткого замыкания (рис. 2.14).
Рис. 2.14. Характеристический треугольник
Катеты ĪКХК
и
ĪKRK
называют соответственно реактивной и активной составляющими напряжения короткого замыкания.При изменении тока нагрузки трансформатора они изменяются пропорционально изменению тока. Это позволяет строить векторные диаграммы для упрощенной схемы замещения трансформатора и производить количественные расчеты. Отношение напряжения
UK =I1HZK
к номинальному напряжению трансформатора UH
,
выраженном в %, называют
относительным напряжением короткого
замыкания при номинальном токе:
uK% = (I1HZK / UH)∙100%.
(2.29)
Относительное напряжение короткого замыкания является важным параметром и указывается в паспорте трансформатора. По известной величине иK%
можно определить установившийся ток короткого замыкания в реальных условиях эксплуатации, т. е. при номинальном напряжении:
I1K = UH/ZK=100I1H / uK%.
(2.30)
Например, установившийся ток короткого замыкания трансформатора, имеющего иK%
= 5 в двадцать раз превышает его номинальное значение, что является недопустимым, поскольку ведет к разрушению трансформатора. Для защиты трансформаторов от токов короткого замыкания в реальных условиях эксплуатации используют автоматические выключатели, которые способны отключить цепь в течение периода. Отметим еще раз: чем больше мощность трансформатора, тем меньше его ток холостого хода и потери в нем, и тем больше ток короткого замыкания.
Таким образом, схема замещения трансформатора дают возможность исследовать его в различных режимах, а опыты холостого хода и короткого замыкания позволяют определить его основные параметры.