Линейные и нелинейные

1. Линейные электрические цепи 2. Нелинейные электрические цепи 3. Расчет нелинейных цепей

Электрической цепью является совокупность элементов и устройств, соединенных проводами и предназначенных для производства, передачи и распределения электрической энергии.

Происходящие в ней электромагнитные процессы рассчитываются при помощи таких параметров, как сила тока, электродвижущая сила, напряжение, сопротивление, емкость и индуктивность. Различают линейные и нелинейные электрические цепи.

Линейные электрические цепи

Линейными электрическими цепями есть такие соединения элементов, когда сопротивление \(R\), индуктивность \(L\) и емкость \(C\) остаются постоянными и не зависят от силы тока и напряжения. Данные элементы являются линейными.

При независимом от напряжения и силы тока сопротивлении, линейную зависимость между этими параметрами показывает закон Ома:

\(u_r=R_x i_r.\)

Вольтамперная характеристика в данном случае будет представлена прямой линией. В том случае, когда индуктивность соленоида не зависима от силы тока, что проходит через нее, потокосцепление ψ будет прямо пропорционально данной силе тока:

\(ψ=Li.\)

При независимой от напряжения \(u_C\) емкости конденсатора C заряд конденсатора будет прямо пропорционален напряжению \(u_C\).

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Решение задач Контрольные работы Эссе

Но линейность вышеуказанных величин – это понятие условное, так как в реальных электрических цепях перечисленные элементы будут нелинейные. К примеру, при протекании электрического тока по резистору, он греется, вследствие чего увеличивается его сопротивление.

Так как в обычном рабочем режиме такие изменения незначительны, ими попросту пренебрегают, считая данные элементы линейными.

Транзисторы, которые функционируют в режиме, когда их вольтамперные характеристики представлены прямыми линиями, условно тоже приравниваются к линейным.

Значит, линейные электрические цепи – это цепи, что включают только линейные элементы. Для их описания используют линейные уравнения.

Нелинейные элементы и их характеристики

Нелинейным элементом электрической цепи называют элемент, сопротивление которого зависит от величины тока, протекающего через нелинейный элемент, или напряжения на выводах нелинейного элемента.

В реальных электрических цепях сопротивления всех элементов носят нелинейный характер, т.к. при протекании тока через элементы цепи в них выделяется различная тепловая мощность. Эта тепловая мощность приводит к изменению температуры элементов цепи, а следовательно, и к изменению их сопротивления. Однако если нелинейность невелика и ею можно пренебречь, то элемент можно считать линейным.

Электрическая цепь называется линейной, если она содержит только линейные элементы, и нелинейной при наличии одного или нескольких нелинейных элементов.

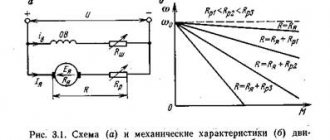
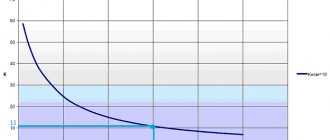
На рисунке 1 представлены вольт-амперные характеристики элементов электрической цепи.

Рисунок 1 – Вольт-амперные характеристики.

Вольт-амперные характеристики (ВАХ) нелинейных элементов делятся на симметричные и несимметричные относительно начала координат.

Симметричные ВАХ

Характеристика 1 представляет собой прямую, проходящую через начало координат и симметричную относительно начала координат. Подобный вид вольт-амперной характеристики имеют линейный пассивные элементы.

Для нелинейных элементов вольт-амперные характеристики будут непрямолинейными. Например, характеристики 2 и 3.

Для симметричной вольт-амперной характеристики нелинейного элемента (характеристики 2 и 3) при изменении полярности напряжения изменится только направление тока на обратное. Симметричные вольт-амперные характеристики имеют например, лампы с металлической нитью или угольной нитью.

Несимметричные ВАХ

Несимметричные вольт-амперные характеристики имеют, например, полупроводниковые элементы: диоды, транзисторы и т.д

Рисунок 2 — Несимметричная ВАХ полупроводникового диода.

Источник

Нелинейные электрические цепи

Нелинейными есть электрические цепи, в которых присутствует один или несколько нелинейных компонентов.
Нелинейные элементы описываются параметрами, зависящими от их определяющих величин. Нелинейные цепи отличаются от линейных некоторыми свойствами. А также в них могут происходить специфические процессы.
Нелинейные элементы описываются статическими \(R_{ст}\), \(L_{ст}\), \(C_ст\) и дифференциальными \(R_д\), \(L_д\), \(C_д\) характеристиками. Статические можно определить соотношением ординаты заданной точки к ее абсциссе, то есть:

\(F_{ст}={y_A\over x_A} .\)

Дифференциальные характеристики рассчитываются как соотношение небольшого приращения его ординаты к соответствующей абсциссе:

\(F_д={dy\over dx}.\)

Методы расчета нелинейных цепей

В теории линейных электрических цепей с постоянными параметрами весь анализ сводится к решению системы линейных дифференциальных или алгебраических уравнений. Математический аппарат для решения подобных уравнений был полностью разработан еще в начале прошлого века. Задача теории в последнее время сводилась к тому, чтобы найти наиболее экономичный и наглядный метод инженерного расчета, анализа или синтеза цепи, в том числе и численных методов. При этом для решения широко применяются принципы наложения и взаимности. Значительно сложнее обстоит дело с расчетом нелинейных электрических цепей. Сама теория нелинейных дифференциальных уравнений, описывающих процессы в нелинейных электрических цепях, разработана значительно меньше. Для нелинейных уравнений каждого типа существуют свои методы подхода и решения, причем многие нелинейные уравнения не имеют аналитических решений, требуют построения специальных функций или применения численных методов. Особенно усложняется расчет нелинейных цепей тем, что в большинстве задач характеристики нелинейного элемента заданы графически и отсутствует достаточно простое и точное математическое описание этих характеристик. Однако инженерная практика требует получения хотя бы грубо ориентировочных расчетных соотношений, которые дают количественную оценку процессов, происходящих в нелинейных цепях. Именно поэтому в отличие от теории линейных цепей, где может быть получено решение задачи с любой точностью, основой теории нелинейных цепей является получение приближенных решений, дающих в основном качественную оценку процессов. Развитие теории нелинейных электрических цепей относится в основном к нынешнему веку. В этой области ведущее значение имеют работы русских и советских ученых А.М. Ляпунова, Л.И. Мандельштама, Н.Д. Папалекси, А.А. Андронова, Н.М. Крылова, Н.Н. Боголюбова и многих других. Из зарубежных работ большое значение для развития нелинейной электротехники имели исследования Пуанкаре, Вандер-Поля, Рюденберга и др. Можно назвать следующие методы приближенного расчета установившихся и переходных процессов в нелинейных цепях, получившие преимущественное распространение в практике инженерных расчетов.

1. Методы малого параметра и условной линеаризации. Одним из методов расчета нелинейной цепи является такое ее упрощение, основанное на пренебрежении относительно малыми величинами, чтобы можно было применять методы расчета линейных цепей, но при решении «квазилинейной» задачи вводить некоторые коррективы, обусловленные нелинейностью. Например, при анализе нелинейных цепей переменного тока, в которых значение высших гармоник относительно невелико, несинусоидальные токи заменяют эквивалентными синусоидальными и применяют комплексный метод расчета, но с учетом нелинейной зависимости между действующими значениями и фазами эквивалентных синусоид тока и напряжения. Разновидностью метода малого параметра является метод гармонического баланса. При расчете цепи этим методом рассматривают амплитуды основных гармонических составляющих токов и напряжений в нелинейной электрической цепи и пренебрегают действием всех высших гармоник. При этом иногда полагают, что амплитуды гармонических составляющих медленно изменяются, но нет необходимости учитывать спектр гармоник, связанных с изменением амплитуды. Такое упрощение задачи по существу является заменой нелинейной зависимости линейной, справедливой только для определенного значения амплитуд тока или напряжения. Поэтому метод условной линеаризации иногда называется методом гармонической линеаризации. Он был применен в работах Л.И. Мандельштама и Н.Д. Папалекси, затем в работах Н.М. Крылова и Н.Н. Боголюбова и получил дальнейшее развитие в работах Л.С. Гольдфарба, Е.П. Попова и других применительно к задачам теории автоматического регулирования. При расчете переходных процессов метод условной линеаризации основывается на приближенной замене нелинейной функции линейной и применении решений линейного уравнения с последующим уточнением результата введением поправок. Этот метод дает очень приближенное решение задачи, однако он наиболее прост и поэтому применяется для ориентировочного расчета процессов, анализ которых более точными методами представляет значительные трудности.

2. Метод аналитической аппроксимации нелинейной характеристики. Сущность метода заключается в приближенном выражении нелинейной характеристики некоторой аналитической функцией такого вида, чтобы достаточно просто решалось нелинейное дифференциальное уравнение цепи. Успешное применение метода зависит от того, насколько точно удалось подобрать аналитическое выражение для нелинейной характеристики и насколько просто решается полученное дифференциальное уравнение. При решении дифференциального уравнения иногда пренебрегают некоторыми членами ввиду их относительной малости, рассматривая их как своего рода малый параметр. Этот метод при расчете нелинейных цепей переменного тока применяется в сочетании с методом гармонической линеаризации и дает возможность аналитически найти первую гармонику тока или напряжения в нелинейной цепи.

3. Метод кусочно-линейной аппроксимации характеристики и припасовывания линейных решений. Сущность метода заключается в замене нелинейной характеристики некоторой ломаной линией и решении задачи методами линейной электротехники. Решения, полученные для каждого из участков ломаной, «припасовываются» одно к другому соответствующим выбором постоянных интегрирования. Метод получил широкое применение для решения самых различных задач.

4. Итерационный метод. Применяя этот метод, сначала находят приближенное решение или задаются им, а затем его уточняют путем многократной подстановки каждого решения в исходное уравнение цепи. Итерационные методы применяются и для численного решения задачи при помощи ЭВМ.

Нелинейные цепи постоянного и переменного тока

Нелинейные элементные и схемные уравнения, обозначения и параметры. Нелинейный — это схема, которая содержит по крайней мере один нелинейный элемент резистивного, емкостного, индуктивного или ЭДС (тока) источника. Для перечисленных нелинейных пассивных элементов вольтамперное напряжение U = fR (I) , висящее напряжение q = fC (u) и ток Вебера Ψ = fL (i) являются нелинейными это.

Для нелинейных источников или для более общих нелинейных активных двухполюсных сетей нелинейная внешняя характеристика U = fÅ (I) . Графическое отображение нелинейных элементов приведено в таблице. 7.1. Второе из двух возможных обозначений нелинейного индуктивного элемента (см. Параграфы 3 и 4 таблицы 7.1), если такой элемент представляет собой катушку с ферромагнитной магнитной цепью, которая определяет нелинейность элемента.

Обратите внимание, что он используется для характеристики нелинейного элемента зависят от скорости изменения переменной.

Следовательно, статическая вольт-амперная характеристика (CVC) резистивного элемента U = fR (I), который связывает постоянный ток и напряжение, является динамической CVC u = ϕR (i) Отличается. Статическое и дифференциальное сопротивление и проводимость определяются по характеристикам I — V.
Статические и динамические характеристики кулоновского напряжения и тока Вебера, статическая и дифференциальная емкость и индуктивность, то есть статические и дифференциальные параметры нелинейных емкостных и индуктивных элементов.

Для описания нелинейных и линейных цепных процессов используются первое и второе уравнения закона Кирхгофа и компонентные уравнения для всех элементов цепочки. Уравнения компонентов включают в себя усилители на болтах, подвески на болтах, усилители Вебера и уравнения для внешних характеристик линейных и нелинейных элементов цепи.

Уравнения, обозначения и параметры нелинейных элементов и цепей

Во многих случаях сами перечисленные свойства используются вместо компонентных уравнений для нелинейных элементов и представлены в графической или табличной форме. Кроме того, для нелинейных элементов такие характеристики должны соответствовать скорости рассматриваемого процесса. Или статический или динамический.

Обратите внимание, что для так называемых инерционных элементов статические и динамические характеристики могут совпадать. Функции режимов и методы расчета нелинейных цепей. Существует несколько возможностей для стационарных нелинейных цепей. Форматы тока и напряжения пассивного устройства в таком режиме обычно отличаются от форматов тока и напряжения источника.

Особенности режимов и методов расчета нелинейных цепей.

В установившихся исследованиях путем плавного изменения отдельных параметров цепи, таких как амплитуда, частота или фаза источника синусоидальной ЭДС, наблюдается много эффектов, которые не распространены в линейных цепях: выходное напряжение или Стабилизация тока (т. Е. Нулевая чувствительность выходного параметра) для изменения параметров входного сигнала), внезапные изменения амплитуды или частоты колебаний выходного тока и напряжения при относительно небольших изменениях параметров входного сигнала.

Основные особенности стационарного расчета в нелинейных цепях заключаются в следующем.

Принцип суперпозиции не может быть применен. В общем случае невозможно найти аналитическое решение. Чтобы оценить не только параметры и характеристики данного элемента, но также и его устойчивость, необходимо также изучить решение в конкретной окрестности изменений этих параметров и характеристик.

Нелинейные цепи постоянного тока

При расчете стационарного режима нелинейной цепи могут быть использованы различные методы, известные из теории линейных цепей: методы эквивалентных генераторов, преобразования электрических цепей, но их реализация характеристик нелинейных элементов. Он выполнен с учетом определенных особенностей. Форма задания характеристик нелинейного элемента (анализ, графика, таблицы, алгоритмы) также влияет на выбор метода и свойства решения.

В то время как достаточно сложные схемы схем рассчитываются численными или аналитическими численными методами, простые схемы схем часто могут быть рассчитаны и исследованы с использованием графических или квазианалитических методов. Нелинейная цепь постоянного тока. Показана схема с известными параметрами элемента. Определить напряжение и ток нелинейного элемента и построить вольт-амперные характеристики участка цепи. Применяются полуаналитические, графические и численные методы.

Алгоритм решения типовых задач приведен в таблице. 7.2. Численный метод расчета нелинейных цепей постоянного тока. Нелинейные цепи постоянного тока описываются нелинейными алгебраическими уравнениями.

Численные методы расчета нелинейных цепей постоянного тока.

Численные методы определения корней нелинейных алгебраических уравнений реализованы в стандартных программах. Обратите особое внимание на схему реализации метода Ньютона (метод дискретной линейной модели). В этом методе на каждом шаге итерации нелинейный резистор представлен линейной эквивалентной схемой.

В приведенной ниже таблице показана эквивалентная схема нелинейного резистора и его компонентное уравнение. 7.3 (где k — номер шага итерации). Нелинейная цепь переменного тока. Основной метод расчета: по току, напряжению, связи потока, мгновенному значению заряда, основной гармонике, в соответствии с текущим значением тока и напряжения.

Расчет основан на мгновенных значениях и основных гармониках. Рассматривается цепь или часть цепи с известной вольт-амперной, веб-амперной или вольт-амперной характеристикой, подключенной к синусоидальному источнику напряжения или тока. Характеристики могут быть заданы в виде графиков, таблиц или функций аппроксимации.