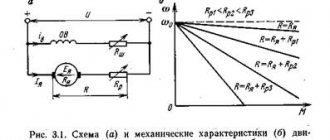
1. Linear electrical circuits 2. Nonlinear electrical circuits 3. Calculation of nonlinear circuits
An electrical circuit is a set of elements and devices connected by wires and designed for the production, transmission and distribution of electrical energy.
The electromagnetic processes occurring in it are calculated using parameters such as current, electromotive force, voltage, resistance, capacitance and inductance. There are linear and nonlinear electrical circuits.
Linear electrical circuits
Linear electrical circuits are connections of elements where resistance \(R\), inductance \(L\) and capacitance \(C\) remain constant and do not depend on current and voltage. These elements are linear.
With resistance independent of voltage and current, a linear relationship between these parameters is shown by Ohm’s law:
\(u_r=R_x i_r.\)
The current-voltage characteristic in this case will be represented by a straight line. In the case when the inductance of the solenoid is independent of the current strength that passes through it, the flux linkage ψ will be directly proportional to the given current strength:
\(ψ=Li.\)
If the capacitance of the capacitor C is independent of the voltage \(u_C\), the charge of the capacitor will be directly proportional to the voltage \(u_C\).
Is it difficult to figure it out on your own?
Try asking your teachers for help
Solving problems Tests Essays
But the linearity of the above quantities is a conditional concept, since in real electrical circuits the listed elements will be nonlinear. For example, when electric current flows through a resistor, it heats up, as a result of which its resistance increases.
Since such changes are insignificant in normal operating mode, they are simply ignored, considering these elements to be linear.
Transistors that operate in a mode where their current-voltage characteristics are represented by straight lines are also conditionally equated to linear.
This means that linear electrical circuits are circuits that include only linear elements. Linear equations are used to describe them.
Nonlinear elements and their characteristics
A nonlinear element of an electrical circuit is an element whose resistance depends on the amount of current flowing through the nonlinear element or the voltage at the terminals of the nonlinear element.
In real electrical circuits, the resistance of all elements is nonlinear, because When current flows through circuit elements, different thermal power is released in them. This thermal power leads to a change in the temperature of the circuit elements, and consequently to a change in their resistance. However, if the nonlinearity is small and can be neglected, then the element can be considered linear .
An electrical circuit is called linear if it contains only linear elements, and nonlinear if it contains one or more nonlinear elements.
Figure 1 shows the current-voltage characteristics of the elements of the electrical circuit.
Figure 1 – Current-voltage characteristics.
Current-voltage characteristics (volt-ampere characteristics) of nonlinear elements are divided into symmetrical and asymmetrical relative to the origin of coordinates.
Symmetrical current-voltage characteristics
Characteristic 1 is a straight line passing through the origin and symmetrical about the origin. have a similar type of current-voltage characteristic .
For nonlinear elements, the current-voltage characteristics will be non-linear . For example, characteristics 2 and 3.
For a symmetrical current-voltage characteristic of a nonlinear element (characteristics 2 and 3), when the voltage polarity changes, only the direction of the current will change to the opposite. For example, lamps with a metal filament or a carbon filament have symmetrical current-voltage characteristics.
Asymmetrical current-voltage characteristics
For example, semiconductor elements have asymmetrical current-voltage characteristics: diodes, transistors, etc.
Figure 2 - Asymmetrical current-voltage characteristic of a semiconductor diode.
Source
Nonlinear electrical circuits
- Nonlinear electrical circuits are those in which one or more nonlinear components are present.
- Nonlinear elements are described by parameters depending on their defining quantities. Nonlinear circuits differ from linear ones in some properties. And also specific processes can occur in them.
- Nonlinear elements are described by static \(R_{st}\), \(L_{st}\), \(C_st\) and differential \(R_d\), \(L_d\), \(C_d\) characteristics. Static can be determined by the ratio of the ordinate of a given point to its abscissa, that is:
\(F_{st}={y_A\over x_A} .\)
- Differential characteristics are calculated as the ratio of a small increment of its ordinate to the corresponding abscissa:
\(F_d={dy\over dx}.\)
Methods for calculating nonlinear circuits
In the theory of linear electrical circuits with constant parameters, the entire analysis comes down to solving a system of linear differential or algebraic equations. The mathematical apparatus for solving such equations was fully developed at the beginning of the last century. The task of the theory in recent times has been to find the most economical and visual method of engineering calculation, analysis or synthesis of a circuit, including numerical methods. In this case, the principles of overlap and reciprocity are widely applied to the solution. The situation with the calculation of nonlinear electrical circuits is much more complicated. The theory itself of nonlinear differential equations describing processes in nonlinear electrical circuits has been developed much less. Nonlinear equations of each type have their own methods of approach and solution, and many nonlinear equations do not have analytical solutions and require the construction of special functions or the use of numerical methods. The calculation of nonlinear circuits is especially complicated by the fact that in most problems the characteristics of a nonlinear element are specified graphically and there is no sufficiently simple and accurate mathematical description of these characteristics. However, engineering practice requires obtaining at least roughly approximate design relationships that provide a quantitative assessment of the processes occurring in nonlinear circuits. That is why, in contrast to the theory of linear circuits, where a solution to a problem can be obtained with any accuracy, the basis of the theory of nonlinear circuits is to obtain approximate solutions that mainly give a qualitative assessment of the processes. The development of the theory of nonlinear electrical circuits relates mainly to the present century. In this area, the works of Russian and Soviet scientists A.M. are of leading importance. Lyapunova, L.I. Mandelstam, N.D. Papaleksi, A.A. Andronova, N.M. Krylova, N.N. Bogolyubov and many others. Among foreign works, the studies of Poincaré, Vander-Poel, Ryudenberg and others were of great importance for the development of nonlinear electrical engineering. The following methods can be mentioned for the approximate calculation of steady-state and transient processes in nonlinear circuits, which have become predominantly widespread in the practice of engineering calculations.
1. Methods of small parameter and conditional linearization. One of the methods for calculating a nonlinear circuit is to simplify it, based on neglecting relatively small quantities, so that it is possible to apply methods for calculating linear circuits, but when solving a “quasi-linear” problem, introduce some adjustments due to nonlinearity. For example, when analyzing nonlinear alternating current circuits in which the value of higher harmonics is relatively small, nonsinusoidal currents are replaced by equivalent sinusoidal ones and a complex calculation method is used, but taking into account the nonlinear relationship between the effective values and phases of the equivalent sinusoids of current and voltage. A variation of the small parameter method is the harmonic balance method. When calculating a circuit using this method, the amplitudes of the main harmonic components of currents and voltages in a nonlinear electrical circuit are considered and the effect of all higher harmonics is neglected. In this case, it is sometimes assumed that the amplitudes of the harmonic components change slowly, but there is no need to take into account the spectrum of harmonics associated with the change in amplitude. This simplification of the problem is essentially the replacement of a nonlinear dependence with a linear one, valid only for a certain value of current or voltage amplitudes. Therefore, the conditional linearization method is sometimes called the harmonic linearization method. It was used in the works of L.I. Mandelstam and N.D. Papaleksi, then in the works of N.M. Krylov and N.N. Bogolyubov and was further developed in the works of L.S. Goldfarb, E.P. Popov and others in relation to problems in the theory of automatic control. When calculating transient processes, the conditional linearization method is based on the approximate replacement of a nonlinear function by a linear one and the application of solutions to a linear equation, followed by refinement of the result by introducing corrections. This method gives a very approximate solution to the problem, but it is the simplest and therefore is used for the approximate calculation of processes, the analysis of which by more accurate methods presents significant difficulties.
2. Method of analytical approximation of a nonlinear characteristic. The essence of the method lies in the approximate expression of the nonlinear characteristic by some analytical function of such a form that the nonlinear differential equation of the circuit can be solved quite simply. The successful application of the method depends on how accurately it was possible to select an analytical expression for the nonlinear characteristic and how simply the resulting differential equation is solved. When solving a differential equation, some terms are sometimes neglected due to their relative smallness, considering them as a kind of small parameter. When calculating nonlinear AC circuits, this method is used in combination with the harmonic linearization method and makes it possible to analytically find the first harmonic of current or voltage in a nonlinear circuit.
3. Method of piecewise linear approximation of characteristics and fitting of linear solutions. The essence of the method is to replace the nonlinear characteristic with a certain broken line and solve the problem using linear electrical engineering methods. The solutions obtained for each section of the broken line are “fitted” one to another by the appropriate choice of integration constants. The method has been widely used to solve a wide variety of problems.
4. Iterative method. Using this method, an approximate solution is first found or specified, and then it is refined by repeatedly substituting each solution into the original circuit equation. Iterative methods are also used to solve problems numerically using a computer.
Nonlinear DC and AC circuits
Nonlinear elemental and circuit equations, notations and parameters. Nonlinear is a circuit that contains at least one nonlinear element of a resistive, capacitive, inductive, or emf (current) source. For the listed nonlinear passive elements, the current-voltage U = fR (I), hanging voltage q = fC (u) and Weber current Ψ = fL (i) are nonlinear.
For nonlinear sources or for more general nonlinear active two-terminal networks, the nonlinear external characteristic is U = fÅ(I). A graphical display of nonlinear elements is given in the table. 7.1. The second of two possible designations for a nonlinear inductive element (see Paragraphs 3 and 4 of Table 7.1), if such an element is a coil with a ferromagnetic magnetic circuit that determines the nonlinearity of the element.
Note that it is used to characterize a nonlinear element dependent on the rate of change of the variable.
- Therefore, the static current-voltage characteristic (CVC) of a resistive element U = fR (I), which couples direct current and voltage, is dynamic CVC u = ϕR (i) Different. Static and differential resistance and conductivity are determined by characteristics I - V.
- Static and dynamic characteristics of Coulomb voltage and Weber current, static and differential capacitance and inductance, that is, static and differential parameters of nonlinear capacitive and inductive elements.
To describe nonlinear and linear chain processes, the first and second equations of Kirchhoff's law and component equations for all elements of the chain are used. Component equations include bolt-on amplifiers, bolt-on hangers, Weber amplifiers, and equations for the external characteristics of linear and nonlinear circuit elements.
Equations, notations and parameters of nonlinear elements and circuits
In many cases, the listed properties themselves are used instead of component equations for nonlinear elements and are presented in graphical or tabular form. In addition, for nonlinear elements such characteristics must correspond to the speed of the process under consideration. Either static or dynamic.
Please note that for so-called inertial elements, static and dynamic characteristics can be the same. Functions of modes and methods for calculating nonlinear circuits. There are several possibilities for stationary nonlinear circuits. The current and voltage formats of the passive device in this mode are usually different from the current and voltage formats of the source.
Features of modes and methods for calculating nonlinear circuits.
In steady-state studies, by smoothly varying individual circuit parameters, such as the amplitude, frequency, or phase of a sinusoidal EMF source, many effects are observed that are not common in linear circuits: output voltage or current stabilization (i.e., zero sensitivity of the output parameter) to change parameters input signal), sudden changes in the amplitude or frequency of fluctuations in output current and voltage with relatively small changes in the parameters of the input signal.
The main features of stationary calculations in nonlinear circuits are as follows.
- The principle of superposition cannot be applied. In general, it is impossible to find an analytical solution. In order to evaluate not only the parameters and characteristics of a given element, but also its stability, it is also necessary to study the solution in a specific vicinity of changes in these parameters and characteristics.
Nonlinear DC Circuits
When calculating the stationary mode of a nonlinear circuit, various methods known from the theory of linear circuits can be used: methods of equivalent generators, transformations of electrical circuits, but their implementation of the characteristics of nonlinear elements. It is made taking into account certain features. The form of specifying the characteristics of a nonlinear element (analysis, graphics, tables, algorithms) also affects the choice of method and properties of the solution.
- While fairly complex circuit designs are calculated using numerical or analytical numerical methods, simple circuit designs can often be calculated and examined using graphical or quasi-analytical methods. Nonlinear DC circuit. A diagram with known element parameters is shown. Determine the voltage and current of the nonlinear element and plot the current-voltage characteristics of the circuit section. Semi-analytical, graphical and numerical methods are used.
The algorithm for solving typical problems is given in the table. 7.2. Numerical method for calculating nonlinear DC circuits. Nonlinear DC circuits are described by nonlinear algebraic equations.
Numerical methods for calculating nonlinear DC circuits.
Numerical methods for determining the roots of nonlinear algebraic equations are implemented in standard programs. Pay special attention to the implementation diagram of Newton's method (discrete linear model method). In this method, at each iteration step, the nonlinear resistor is represented by a linear equivalent circuit.
- The table below shows the equivalent circuit of a nonlinear resistor and its component equation. 7.3 (where k is the iteration step number). Nonlinear AC circuit. Basic calculation method: according to current, voltage, flux coupling, instantaneous charge value, fundamental harmonic, according to the current value of current and voltage.
The calculation is based on instantaneous values and fundamental harmonics. Consider a circuit or part of a circuit with a known current-voltage, web-ampere, or current-voltage characteristic connected to a sinusoidal voltage or current source. Characteristics can be specified in the form of graphs, tables or approximation functions.