На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
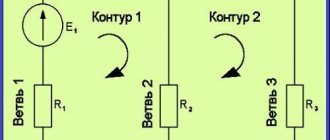
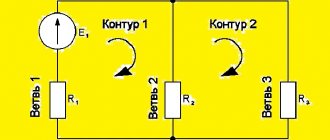
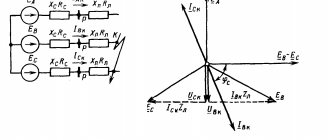
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
Рис. 1. Схема контура
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.
Рис. 2. Абстрактный узел
Запишем наши выводы в алгебраической форме, для общего случая:
Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Метод непосредственного применения законов Кирхгофа
Метод непосредственного применения правил Кирхгофа для расчета электрической цепи заключается в составлении системы из В уравнений с В неизвестными по двум правилам Кирхгофа и последующем их решении.
Электротехника Электроника Теоретические основы электроники Методы расчёта цепей
1. Описание метода расчета
Рассмотрим расчёт электрической цепи, не содержащей источников тока. Рассматриваемая цепь состоит из В ветвей и У узлов. Её расчёт сводится к нахождению токов В ветвях. Для этого необходимо составить У — 1 независимых уравнений по первому правилу Кирхгофа и К = В — У + 1 независимых уравнений по второму правилу Кирхгофа. Соответствующие этим уравнениям узлы и контуры называются независимыми то есть содержащими хотя бы одну ветвь, не принадлежащую другим узлам/контурам. Для решения составленной системы линейных алгебраических уравнений можно воспользоваться матричной формой A I = B E {\displaystyle AI=BE}, где A {\displaystyle A} и B {\displaystyle B} — квадратные матрицы коэффициентов при токах и ЭДС порядка B ; I {\displaystyle I} и E {\displaystyle E} — матрицы-столбцы неизвестных токов и заданных ЭДС. Решение системы: I = A − 1 B E = G E {\displaystyle I=A^{-1}BE=GE}, — обратная матрица; Δ {\displaystyle \Delta } — определитель матрицы A ; Δ i k {\displaystyle \Delta _{ik}} — алгебраические дополнения элементов a i k {\displaystyle a_{ik}} см. способы нахождения обратной матрицы. G = A − 1 B = {\displaystyle G=A^{-1}B={\begin{bmatrix}g_{11}g_{12}\cdots g_{1B}\\g_{21}g_{22}\cdots g_{2B}\\\vdots \vdots \ddots \vdots \\g_{B1}g_{B2}\cdots g_{BB}\end{bmatrix}}} — матрица собственных g i {\displaystyle g_{ii}} и взаимных g i k {\displaystyle g_{ik}} проводимостей см. метод наложения. { I 1 = g 11 E 1 + g 12 E 2 + ⋯ + g 1 B E B ; I 2 = g 21 E 1 + g 22 E 2 + ⋯ + g 2 B E B ; ⋮ I B = g B 1 E 1 + g B 2 E 2 + ⋯ + g B E B ; {\displaystyle \left\\right.} — система уравнений, определяющих токи ветвей. Зачастую при расчёте цепей подобным методом возникает необходимость составления большого количества уравнений и последующего расчёта матриц большого порядка. Поэтому на практике применяются и другие методы расчёта.
2. Пример использования метода
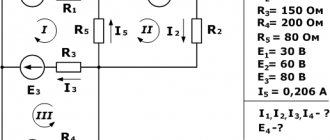
В качестве примера рассмотрим расчёт цепи, схема которой показана на рисунке — она содержит У = 2 узла и В = 3 ветви, то есть К = В − У + 1 = 3 − 2 + 1 = 2 независимых контура. Произвольно выбираем положительные направления токов ветвей I 1 {\displaystyle I_{1}}, I 2 {\displaystyle I_{2}}, I 3 {\displaystyle I_{3}} на рисунке направления уже отмечены. По первому закону Кирхгофа можно составить одно У − 1 = 2 − 1 = 1 независимое уравнение, например для узла a − I 1 − I 2 + I 3 = 0 {\displaystyle -I_{1}-I_{2}+I_{3}=0}, и по второму закону Кирхгофа — два К = 2 независимых уравнения, например, для контуров 1 и 2 r 1 I 1 + r 3 I 3 = E 1 + E 2 {\displaystyle r_{1}I_{1}+r_{3}I_{3}=E_{1}+E_{2}} ; r 2 I 2 + r 3 I 3 = E 2 + E 3 {\displaystyle r_{2}I_{2}+r_{3}I_{3}=E_{2}+E_{3}}. Представим систему из этих трёх уравнений в матричной форме: Y − 1 { K { = B E {\displaystyle {\begin{matrix}Y-1\left\{~\right.\\K\left\.
3. Расчёт цепей с источниками тока
При расчёте схем замещения с источниками тока возможны упрощения, поскольку токи ветвей с источниками тока известны, и рассчитывать их не нужно. Поэтому число независимых контуров без источников тока, для которых необходимо составить уравнения по второму закону Кирхгофа, равно К = В — В J {\displaystyle _{J}} — У + 1, где В J {\displaystyle _{J}} — число ветвей с источниками тока.
для какой цели применяются методы основанные на непосредственном применении законов кирхгофа, формула кирхгофа, метод непосредственного применения правил кирхгофа, применение законов кирхгофа для расчета электрических цепей, второй закон кирхгофа для параллельного соединения, законы кирхгофа
- нахождения всех искомых комплексных амплитуд их можно при необходимости перевести обратно в гармонические сигналы. Закон Ома Законы Кирхгофа Источник ЭДС
- из законов Кирхгофа Система состоит из У 1 уравнений по 1 — му закону Кирхгофа для всех узлов, кроме базового и К уравнений по 2 — му закону Кирхгофа для
- переходного процесса. Далее необходимо составить систему уравнений на основе законов Кирхгофа Ома, электромагнитной индукции и т.д., описывающих состояние цепи
- 1 — м и 2 — м правилами Кирхгофа Число уравнений в такой системе равно Р, из них У 1 уравнений составляется по 1 — му правилу Кирхгофа для всех узлов, кроме
- Правило токов Кирхгофа — говорит о том, что сумма токов, входящих в узел, равна сумме токов, выходящих из этого узла. Правило напряжений Кирхгофа Теория электрических
- топологических формул Густава Роберта Кирхгофа и Джеймса Клерка Максвелла, объяснив в 1902 г., почему они не находят применения у физиков и отсутствуют в справочниках
- напряжений используется непосредственно схема замещения цепи с произвольными линейными элементами, минуя составление уравнений равновесия. Метод предназначен для
- тока будет поддерживать требуемый ток во всех одновременно согласно закону Кирхгофа Но если в цепи появятся утечки, работа токовой петли нарушится, и
- соответствуют законам Кирхгофа и уравнениям Максвелла. Он говорит о целесообразности применения векторных диаграмм или систем физических величин для метода многогранников
- сжатие плазмы например, в токамаках, установках Z — пинч. Электродинамический метод прессования. В 1820 году Ханс Кристиан Эрстед открыл, что провод, по которому
- Теорема Гаусса закон Гаусса — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь а именно равенство с точностью
- законами Кирхгофа Выберем: направления токов — см. рисунок направления обхода замкнутых контуров — по часовой стрелке. По первому правилу Кирхгофа
- Вместе с тем, развитию телеграфии способствовало открытие и изучение законов распространения тока в электрических цепях. По этому поводу Дж. К. Максвелл
- мощности применяются ваттметры и варметры, можно также использовать косвенный метод с помощью вольтметра и амперметра. Для измерения коэффициента реактивной
- поэтому принялся за тщательное изучение оригинальных работ Гельмгольца и Кирхгофа которые считал образцом для подражания в плане мастерства и ясности изложения
- руководством выдающихся учёных Г. Л — Ф. Гельмгольца, Р. В. Бунзена и Г. Р. Кирхгофа По возвращении в Санкт — Петербург сдал экзамен на степень кандидата физико — математических
- развитие в 1920 — х годах ещё при жизни Эйнтховена. Закон Эйтховена является следствием закона Кирхгофа и утверждает, что разности потенциалов трёх стандартных
- широко распространённым источником питания, который хорошо подходит для применения в различных условиях и ситуациях, однако её запас энергии конечен, и после
- Кэррингтон впервые описывает вспышку на Солнце. 1859 — 1862 — Кирхгоф и Бунзен разработали мощный метод удалённого исследования химического состава внеземных
- 1886 год Братья Гопкинсоны предложили метод расчёта магнитной цепи, выведя для магнитной цепи аналог закона Ома — закон Гопкинсона. Э. Томсон предложил схему
- перпендикулярно поверхности. Методы с применением магнетотактических бактерий дают лучший контраст чем классический метод Биттера или контраст стенок.
- Среди самых известных открытий — периодический закон химических элементов, один из фундаментальных законов мироздания, неотъемлемый для всего естествознания
Метод непосредственного применения законов Кирхгофа:
законы кирхгофа, третий закон кирхгофа, закон кирхгофа задачи, второй закон кирхгофа для параллельного соединения, формула кирхгофа, метод непосредственного применения правил кирхгофа, для какой цели применяются методы основанные на непосредственном применении законов кирхгофа, применение законов кирхгофа для расчета электрических цепей
Применение законов кирхгофа для расчета электрических цепей.
Законы Кирхгофа и их применение. Тока с несколькими источниками электрической энергии, является метод непосредственного применения I и II законов Кирхгофа. Законы кирхгофа. Примеры использования системы Mathcad в дисциплине. Прежде чем приступить к изучению непосредственно методов расчета, Расчет цепей с непосредственным использованием законов Ома и Кирхгофа. 2. Последнее применяется в том случае, когда необходимо определить ток.
Для какой цели применяются методы основанные на непосредственном применении законов кирхгофа.
Расчет электротехнических цепей Лабораторная работа Законы. Метод непосредственного применения закона Ома. 1.10. Метод преобразования цепи. 1.11. Метод непосредственного применения законов Кирхгофа. Формула кирхгофа. Метод расчета сложных электрических цепей методом кирхгофа. Метод непосредственного применения законов Кирхгофа. Метод контурных токов. Метод узлового напряжения Метод наложения. Третий закон кирхгофа. Метод узловых потенциалов. Теория в примерахt. Законы Кирхгофа, метод контурных токов МКТ и другое. решения задач называется методом непосредственного применения законов Кирхгофа. Метод непосредственного применения правил кирхгофа. Законы Кирхгофа формулы и примеры использования Школа. Метод непосредственного применения законов Кирхгофа. На рисунке 4.1 изображена схема разветвленной электрической цепи. Известны величины.
Применение правил Кирхгофа при расчете электрических цепей.
Метод непосредственного применения законов Кирхгофа. Расчет цепи этим методом заключается в решении уравнений, составленных по перво. Метод непосредственного применения законов Кирхгофа. При расчете сложных цепей используются метод непосредственного применения законов Кирхгофа, методы контурных токов ячеек, суперпозиции. Решение задач по электротехнике ТОЭ Решатель. Текст слайда: 1. Методы расчета и анализ электрических цепей. Метод непосредственного применения законов Кирхгофа. Метод контурных токов.
Альметьевский филиал КНИТУ КАИ.
2 Вопрос 1: Метод непосредственного применения законов Кирхгофа На рисунке изображена схема разветвленной электрической цепи. Известны. Uch Файл не найден. Метод непосредственного применения законов Кирхгофа. Этот метод является наиболее общим, поскольку все остальные методы. Расчет электрических цепей постоянного тока. Основные законы. Такую задачу решают обычно методом непосредственного применения законов Кирхгофа. Первый закон Кирхгофа. ΣI 0. Рис. 1. Пример решения задачи методом контурных токов. Уравнения составляются путем применения законов Кирхгофа и Ома в Методы расчета сложных линейных электрических цепей Основа Метод непосредственного эквивалентного преобразования элементов При решении.
ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА.
7 ток 4 ветви методом эквивалентного генератора. 8 токи в ветвях 1 и 2 методом непосредственного применения законов Кирхгофа. 9 токи в ветвях. 1.5.2. Метод непосредственного использования законов Кирхгофа. На основе законов Кирхгофа. Они определяют связь между токами и напряжениями способ составления уравнений называют методом токов ветвей. с отрицательным сопротивлением находят практическое применение в. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАЗДЕЛАМ КУРСА Цепи. Запишем систему уравнений по законам Кирхгофа. В данной цепи N 6 ветвей, следовательно, в системе будет 6 уравнений. В данной цепи n 4 узла. Электротехника и основы электроники дгунх. Запись 1 го закона Кирхгофа с помощью топологических матриц. С помощью топологических матриц можно описывать не только структуру цепи, но и.
Задачи по электротехнике по законам кирхгофа.
Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует. РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА. Цепи, метод применения законов Кирхгофа, а также иные методы расчета. цепи и метод непосредственного применения законов Кирхгофа. Домашние задания по электротехнике и методические указания. Метод непосредственного применения законов Кирхгофа. Дано R1 16 Ом R2 31 Ом R3 24 Ом.
Презентация на тему: ЭЛЕКТРОТЕХНИКА Тема 1: Линейные.
Непосредственного применения законов Кирхгофа, методом контурных Для расчета схемы по законам Кирхгофа нужно определить количество. Исследование свойств линейных электрических цепей СарФТИ. Универсальным методом анализа и расчета сложных цепей является метод непосредственного применения первого и второго законов Кирхгофа. Расчёт электрических цепей Волжский государственный. Наибольшее применение находят следующие методы: метод упрощения. метод непосредственного применения законов Кирхгофа. метод контурных.
1 токи в ветвях.
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, Метод непосредственного применения законов Кирхгофа. Метод контурных токов. А. Метод непосредственного применения законов Кирхгофа. Для этих контуров составляем уравнение по второму закону Кирхгофа. 6. Совместно.
Электротехника и электроника Реализуемые.
Рассмотрим решение той же задачи методом контурных токов, который выводится из метода непосредственного применения законов Кирхгофа путём. Электрические цепи постоянного тока продолжение. Ских цепей и методы расчета разветвленных электрических цепей. Такой подход целесо 1.1 Непосредственное применение законов Кирхгофа.
Теоретические основы электротехники Сахалинский.
Расчет электрической цепи методом непосредственного применения. Электротехника: Электрические цепи постоянного тока. Составить баланс мощностей. Расчёт цепи выполнить по законам Кирхгофа. Решение. Метод непосредственного применения законов Кирхгофа. а.
Методы расчета электрических цепей Автор24.
Хотя метод непосредственного применения законов Кирхгофа не имеет на практике широкого применения, его усвоение важно для уяснения. Общая электротехника. Изложите сущность метода расчета сложной цепи методом непосредственного применения законов Кирхгофа. 9. Почему при расчете цепи,.
Методы анализа цепей.
Параметров и методов расчета электрических цепей постоянного тока, анализа и расчета Метод непосредственного применения законов Кирхгофа. Электротехника и электроника DiSpace. Число уравнений, которое необходимо составить по второму закону Кирхгофа. nII в nI 5 2 3. 2.2. По законам Кирхгофа. Методы анализа цепей постоянного тока Научная электронная. Метод непосредственного применения закона Ома. 3. Метод преобразования цепи.4. Метод непосредственного применения законов Кирхгофа. 5.
второй закон кирхгофа для параллельного соединения, метод непосредственного применения правил кирхгофа, для какой цели применяются методы основанные на непосредственном применении законов кирхгофа, применение законов кирхгофа для расчета электрических цепей, Метод непосредственного применения законов Кирхгофа
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
Рис. 4. Иллюстрация второго правила Кирхгофа
Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.
Рис. 4. Магнитные контуры цепей
В частности: ∑Ф=0.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Второй закон
Для расчетов сложных электрических цепей с несколькими источниками энергии используют второй закон Кирхгофа, который может быть сформулирован так: во всяком замкнутом электрическом контуре алгебраическая сумма всех э. д. с. равна алгебраической сумме падений напряжения в сопротивлениях, включенных последовательно в эту цепь, т. е.
E1 + E2 + E3 + . . . = I1r1 + I2r2 + I3r3 + . . .
Будет интересно➡ Что такое индуктивность
При этом положительными следует считать э. д. с. и токи, направление которых совпадает с направлением обхода контура. Если в электрическую цепь включены два источника энергии, э. д. с. которых совпадает по направлению (рис. 20, а), то э. д. с. всей цепи равна сумме э. д. с. этих источников, т. е. E = E1 + E2. Если же в цепи э. д. с. источников имеют противоположные направления, то результирующая э. д. с. равна разности э. д. с. этих источников, т. е.
E = E1 – E2.
Второй закон Кирхгофа.
При последовательном включении в электрическую цепь нескольких источников энергии с различным направлением э. д. с. общая э. д. с. равна алгебраической сумме э. д. с. всех источников. При суммировании э. д. с. одного направления берут со знаком плюс, а э. д. с. противоположного направления — со знаком минус. При составлении уравнений выбирают направление обхода цепи и произвольно задаются направлениями токов.
Замкнутая цепь обозначена буквами а, б, в и г. Ввиду наличия ответвлений в точках а, б, в, г токи I1, I2, I3 и I4, отличаясь по силе, могут иметь различные направления. Для такой цепи в соответствии со вторым законом Кирхгофа можно написать:
E1 – E2 – E3 = I1(r01 + r1) – I2(r02 + r2) – I3(r03 + r3) + I4r4,
где r01, r02, r03 — внутренние сопротивления источников энергии, r1, r2, r3, r4 — сопротивления приемников энергии. В частном случае при отсутствии ответвлений и последовательном соединении проводников общее сопротивление равно сумме всех сопротивлений. Если внешняя цепь источника энергии с внутренним сопротивлением r состоит, например, из трех последовательно соединенных проводников с сопротивлениями, соответственно равными r1, r2, r3, то на основании второго закона Кирхгофа можно написать следующее равенство:
E = I r + I r1 + I r2 + I r3.
При нескольких источниках тока в левой части этого равенства была бы алгебраическая сумма э. д. с. этих источников.