В соответствии с ПУЭ (п 1.2.18-20) в отношении обеспечения надежности электроснабжения электроприемники разделяются на три категории.
Электроприемники 1 категории — это такие устройства, перерыв электроснабжения которых может повлечь за собой опасность для жизни людей, значительный ущерб народному хозяйству, повреждение дорогостоящего основного оборудования, массовый брак продукции, расстройство сложного технологического процесса, нарушение функционирования особо важных элементов коммунального хозяйства. Питание таких электроприемников должно обеспечиваться от двух независимых источников, перерыв допускается лишь на время автоматического восстановления питания.
Классификация электроприемников по обеспечению надежности электроснабжения
В отношении обеспечения надежности электроснабженияэлектроприемники разделяются на следующие три категории:
Электроприемники I категории – электроприемники, перерыв электроснабжения которых может повлечь за собой: опасность для жизни людей, значительный ущерб народному хозяйству, повреждение дорогостоящего основного оборудования, массовый брак продукции, расстройство сложного технологического процесса, нарушение функционирования особо важных элементов коммунального хозяйства.
Из состава электроприемников I категории выделяется особая группа электроприемников, бесперебойная работа которых необходима для безаварийного останова производства с целью предотвращения угрозы жизни людей, взрывов, пожаров и повреждения дорогостоящего основного оборудования.
Электроприемники II категории – электроприемники, перерыв электроснабжения которых приводит к массовому недоотпуску продукции, массовым простоям рабочих, механизмов и промышленного транспорта, нарушению нормальной деятельности значительного количества городских и сельских жителей.
Электроприемники III категории– все остальные электроприемники, не подходящие под определения I и II категорий. Это приемники вспомогательных цехов, несерийного производства продукции и т.п.
Электроприемники I категории должны обеспечиваться электроэнергией от двух независимых взаимно резервирующих источников питания, и перерыв их электроснабжения при нарушении электроснабжения от одного из источников питания может быть допущен лишь на время автоматического восстановления питания. Для электроснабжения особой группы электроприемников I категории должно предусматриваться дополнительное питание от третьего независимого взаимно резервирующего источника питания.
Элементы электрической цепи, осуществляющие преобразование различных видов энергии в электромагнитную, расходуемую и запасаемую в других элементах, называются источниками (генераторами) или активными элементами
цепи. Элементы, осуществляющие необратимое потребление электромагнитной энергии или ее накопление, являются
пассивными элементами.
Простейшие элементы цепи, связанные с остальными двумя выводами, называются
двухполюсниками
.
Пассивные элементы. Необратимое потребление энергии осуществляется в резистивном элементе R
(Табл. 1.1, строка 1). При согласованных направлениях отсчета тока и напряжения, указанных на рисунке, связь между ними выражается
законом Ома
:
uR = Ri
, где
R
—сопротивление элемента — параметр, определяющий интенсивность потребления энергии. Часто используется и обратное соотношение
iR = Gu
, где
G =
1/
R
— проводимость элемента. Потребляемая резистором мощность и энергия положительны:
Накопление энергии в магнитном поле осуществляется в индуктивном элементе L
(Табл. 1.1, строка 2), в котором при протекании тока
i
, изменяющемся во времени, изменяется потокосцепление и наводится ЭДС ( ). Параметр
L
—
индуктивность
—определяет интенсивность накопления энергии. Для преодоления ЭДС
e
к зажимам элемента от внешних источников должно быть приложено напряжение .Индуктивный элемент потребляет энергию при положительных значениях , когда энергия магнитного поля возрастает, и отдает ее при .
Процесс накопления энергии в электрическом поле осуществляется в емкостном элементе C
(Табл. 1.1, строка 3), ток которого
i = dq/dt
определяется скоростью изменения заряда на обкладках элемента, связанного с напряжением между обкладками выражением
q
=
CuC
, где
C
—
емкость
элемента, определяющая интенсивность накопления энергии. Элемент потребляет энергию при и отдает ее при .
Зависимости u
(
i
) резистора, Y(
i
) индуктивной катушки,
q
(
u
) конденсатора —
характеристики элементов
—в общем случае нелинейны. Обладающие такими характеристиками элементы называются
нелинейными
. При линейности соответствующей характеристики параметры
R
,
L
или
C
постоянны, и элементы называются
линейными
. Связи между напряжением и током линейного индуктивного и емкостного элементов указаны в Табл. 1.1. Цепь, составленная целиком из линейных элементов, называется
линейной
. Описывающие ее дифференциальные или алгебраические уравнения являются линейными. Энергия, накапливаемая в линейных элементах
L
и
C
, дана выражениями, приведенными в Табл. 1.1.
Таблица 1.1
| элемент | схема | напряжение | ток | энергия |
| резистивный | u = Ri | i = Gu | ||
| индуктивный | ||||
| емкостной |
Активные элементы. Реальные источники энергии часто работают в одном из следующих режимов: 1) во всем диапазоне допустимых значений тока напряжение на зажимах мало зависит от протекающего тока; 2) наоборот, в рабочем диапазоне ток, генерируемый источником. мало зависит от напряжения на его зажимах.
| Рис. 1.2 | Идеализация свойств источников 1-го типа приводит к источнику ЭДС — элементу, напряжение на зажимах которого не зависит от протекающего через этот источник тока. Стрелка внутри кружка, схематически изображающего источник ЭДС (рис. 1.2, а ), показывает направление действия ЭДС — направление, в котором за счет преобразования энергии осуществляется перемещение положительных зарядов внутри источника. В результате вне источника между его зажимами возникает напряжение. |
Для изображенного стрелкой на рис. 1.2, а
направления отсчета напряжения имеем
u
=
e
. Принятое направление отсчета
u
соответствует направлению линий напряженности электрического поля, возникающего в окружающем источник пространстве. Если к зажимам источника присоединить пассивный элемент, то это электрическое поле вызовет движение положительных зарядов во внешней цепи — электрический ток
i
в направлении стрелки.
Идеализация свойств источника 2-го типа — это источник тока
(рис. 1.2,
б
), ток которого
J
не зависит от напряжения
u
на его зажимах.
Для описания свойств компонентов электронных цепей (например, транзисторов) вводят управляемые (зависимые) источники
, параметры которых зависят от напряжений или токов на других участках рассматриваемой электрической цепи. Существуют четыре типа управляемых источников:
| Рис. 1.3 | 1) Источник напряжения, управляемый напряжением (ИНУН), или усилитель напряжения, ЭДС которого пропорциональна напряжению uab между точками a и b цепи (рис. 1.3, а ). Другой способ схемного изображения усилителя напряжения приведен на рис. 1.4, а . Он эквивалентен рис. 1.3, а и предполагает, что ток во входной ветви |
усилителя i
вх = 0 — входное сопротивление усилителя бесконечно, а напряжение на выходе
i
вых =
ku
вх не зависит от присоединенной нагрузки — выходное сопротивление равно нулю. 2) Источник тока, управляемый напряжением (ИТУН), ток которого пропорционален напряжению
uab
на другом участке (рис. 1.3,
б
). 3) Источник напряжения, управляемый током (ИНУТ), ЭДС которого пропорциональна току
iab
на каком-либо участке (рис. 1.3,
в
). 4) Источник тока, управляемый током (ИТУТ), или усилитель тока, ток которого
J
пропорционален току другого участка цепи
iab
(рис. 1.3,
г
).
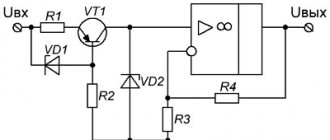
Разновидностью усилителя напряжения является операционный усилитель (ОУ). Он усиливает разность напряжений uab
=
ua
–
ub
, приложенных к входным узлам (рис. 1.4,
б
).
Рис. 1.4
Вход b
, полярность напряжения которого изменяется усилителем, называется инвертирующим, вход
a
— неинвертирующим. Выходное напряжение такого усилителя равно
u
вых =
k
(
ua
–
ub
). С учетом того, что коэффициент усиления
k
операционных усилителей достигает значений 104 – 106, часто принимается идеализация, связанная с допущением о бесконечном значении коэффициента усиления операционного усилителя. Однако, поскольку при
k
® ¥ выходное напряжение остается ограниченным, принятая идеализация ведет к требованию равенства напряжений входных узлов
a
и
b
. Таким образом, для идеального ОУ с
k
= ¥ имеем следующие условия:
ua
=
ub
;
ia
= 0;
ib
= 0.
Рассмотренные типы элементов являются идеализированными моделями компонентов электрических цепей — резистора, катушки индуктивности, конденсатора, источника энергии. С их помощью можно также отобразить второстепенные, или, как иногда говорят, «паразитные» явления, имеющие место в других компонентах реальных электромагнитных устройств и в окружающем их пространстве. Более полную модель можно построить, путем соединения отдельных элементов в так называемую схему замещения рассматриваемого устройства.
Отметим, что введенный набор трех идеальных пассивных элементов, а также независимых и управляемых источников позволяет создавать схемные модели практически любых электромагнитных приборов и устройств, с которыми мы встречаемся на практике
5.ОТВЕТИЛ Топологические понятия теории электрических цепей: узел, ветвь, контур, главные контуры. Законы Кирхгофа.
Топология электрической цепи
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
| Рис.1 | Рис.2 |
Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1
и
3
. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.
3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
Рис.4
4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.
Если граф содержит m
узлов и
n
ветвей, то число ветвей любого дерева , а числа ветвей связи графа .
5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.
Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1
и
S2
. При этом получаем соответственно сечения, образованные ветвями
6-4-5
и
6-2-1-5.
С понятием дерева связаны понятия главных контуров и сечений:
- главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;
- главное сечение– сечение, состоящее из ветвей связи и только одной ветви дерева.
Топологические матрицы
Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.
1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.
Для графа на рис. 3 имеем число узлов m=4
и число ветвей
n=6.
Тогда запишем матрицу
АН , принимая, что элемент матрицы (i
–номер строки;
j
–номер столбца) равен
1
, если ветвь
j
соединена с узлом
i
и ориентирована от него,
-1
, если ориентирована к нему, и
0
, если ветвь
j
не соединена с узлом
i
. Сориентировав ветви графа на рис. 3, получим
.Данная матрица АН записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы АН всегда равна нулю, так как каждый столбец содержит один элемент +1
и один элемент
-1
, остальные нули.
Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы АН путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим
.Число строк матрицы А равно числу независимых уравнений для узлов , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.
Первый закон Кирхгофа
Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение
| (1) |
где — вектор плотности тока; — нормаль к участку dS
замкнутой поверхности
S.
Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S2
графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать
.
Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:
| (2) |
т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.
При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1)
узлов, так как при записи уравнений для всех
m
узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.
Введем столбцовую матрицу токов ветвей
| I= |
Тогда первый закон Кирхгофа в матричной форме записи имеет вид:
| АI=O | (3) |
– где O— нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А,
а не
АН, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1)
узлов.
В качестве примера запишем для схемы на рис. 3
Отсюда для первого узла получаем
,
что и должно иметь место.
2. Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы В
соответствуют контурам, а столбцы – ветвям схемы.
Элемент bij
матрицы
В равен 1
, если ветвь
j
входит в контур
i
и ее ориентация совпадает с направлением обхода контура,
-1
, если не совпадает с направлением обхода контура, и
0
, если ветвь
j
не входит в контур
i.
Матрицу В,
записанную для главных контуров, называют
матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4, запишем коэффициенты для матрицы В.
.
Перейдем теперь ко второму закону Кирхгофа.
Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.
| (4) |
Просуммируем напряжения на ветвях некоторого контура:
Поскольку при обходе контура потенциал каждой i
-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.
Таким образом, второй закон Кирхгофа математически записывается, как:
| (5) |
— и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1)
уравнений, составленных по первому закону Кирхгофа, получаем систему из уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
Введем столбцовую матрицу напряжений ветвей
| U= |
Тогда второй закон Кирхгофа в матричной форме записи имеет вид
| BU = 0. | (6) |
В качестве примера для схемы рис. 5 имеем
,
откуда, например, для первого контура получаем
,
что и должно иметь место.
Если ввести столбцовую матрицу узловых потенциалов
| = |
причем потенциал последнего узла , то матрица напряжений ветвей и узловых потенциалов связаны соотношением
| U=AТ | (7) |
где AТ
— транспонированная узловая матрица.
Для определения матрицы В по известной матрице А=АДАС ,
где
АД
– подматрица, соответствующая ветвям некоторого дерева,
АС
— подматрица, соответствующая ветвям связи, может быть использовано соотношение
В= (-АТСА-1ТД1).
3. Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а столбцы – ветвям графа.
Матрица Q, составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Qравно числу независимых сечений.
Элемент qij
матрицы
Q равен 1
, если ветвьвходит в
i
-е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него),
-1
, если ориентирована противоположно направлению сечения, и
0
, если ветвь
j
не входит в
i
-е сечение.
В качестве примера составим матрицу Qглавных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеем
В заключение отметим, что для топологических матриц А, В
и
Q, составленных для одного и того же графа, выполняются соотношения
| АВТ= 0; | (8) |
| QВТ= 0, | (9) |
которые, в частности, можно использовать для проверки правильности составления этих матриц. Здесь 0 – нулевая матрица порядка .
Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических матриц, по ее структуре можно восстановить остальные.
Литература
1. Теоретические основы электротехники. Т.1. Основы теории линейных цепей./Под ред. П.А.Ионкина. Учебник для электротехн. вузов. Изд.2-е , перераб. и доп. –М.: Высш. шк., 1976.-544с.
2. Матханов Х.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. и радиотехн. спец. 3-е изд. переработ. и доп. –М.: Высш. шк., 1990. –400с.
3. Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
1. Сформулируйте основные топологические понятия для электрических цепей.
2. Что такое узловая матрица?
3. Что такое контурная матрица?
4. Что такое матрица сечений?
5. Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе независимых уравнений:
.
Восстановив граф цепи, составить матрицы главных контуров и сечений, приняв, что ветвям дерева присвоены первые номера.
Ответ:
| B= | Q= |
6. Составить матрицу главных контуров для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5
Ответ:
| B= |
7. Решить задачу 5, используя соотношения (8) и (9).
6. Основные принципы и теоремы электротехники (на примере цепи постоянного тока).
7.ОТВЕТИЛ Основные законы электротехники (на примере цепи постоянного тока).
ЗАКОН ОМА (по имени немецкого физика Г. Ома (1787-1854)) – единица электрического сопротивления. Обозначение Ом. Ом – сопротивление проводника, между концами которого при силе тока 1 А возникает напряжение 1 В. Определяющее уравнение для электрического сопротивления R= U / I.
Закон Ома является основным законом электротехники, без которого нельзя обойтись при расчете электрических цепей. Взаимосвязь между падением напряжения на проводнике, его сопротивлением и силой тока легко запоминается в виде треугольника, в вершинах которого расположены символы U, I, R.
К закону Ома
Самый главный закон электротехники — закон Ома
ЗАКОН ДЖОУЛЯ-ЛЕНЦА (по имени английского физика Дж.П.Джоуля и русского физика Э.Х.Ленца) – закон, характеризующий тепловое действие электрического тока.
Согласно закону, количество теплоты Q (в джоулях), выделяющейся в проводнике при прохождении по нему постоянного электрического тока, зависит от силы тока I (в амперах), сопротивления проводника R (в омах) и времени его прохождения t (в секундах): Q = I2Rt.
Преобразование электрической энергии в тепловую широко используется в электрических печах и различных электронагревательных приборах. Тот же эффект в электрических машинах и аппаратах приводит к непроизвольным затратам энергии (потере энергии и снижении КПД). Тепло, вызывая нагрев этих устройств, ограничивает их нагрузку. При перегрузке повышение температуры может вызвать повреждение изоляции или сокращение срока службы установки.
ЗАКОН КИРХГОФА (по имени немецкого физика Г.Р.Кирхгофа (1824-1887)) – два основных закона электрических цепей. Первый закон устанавливает связь между суммой токов, направленных к узлу соединения (положительные), и суммой токов, направленных от узла (отрицательные).
Алгебраическая сумма сил токов In, сходящихся в любой точке разветвления проводников (узле), равна нулю, т.е. SUMM(In)= 0. Например, для узла A можно записать: I1 + I2 = I3 + I4 или I1 + I2 – I3 – I4 = 0.
Узел тока
Второй закон устанавливает связь между суммой электродвижущих сил и суммой падений напряжений на сопротивлениях замкнутого контура электрической цепи. Токи, совпадающие с произвольно выбранным направлением обхода контура, считаются положительными, а не совпадающие – отрицательными.
Контур тока
Алгебраическая сумма мгновенных значений ЭДС всех источников напряжения в любом контуре электрической цепи равна алгебраической сумме мгновенных значений падений напряжений на всех сопротивлениях того же контура SUMM(En)=SUMM(InRn). Переставив SUMM(InRn) в левую часть уравнения, получим SUMM(En) – SUMM(InRn) = 0. Алгебраическая сумма мгновенных значений напряжений на всех элементах замкнутого контура электрической цепи равна нулю.
Законы Кирхгофа
ЗАКОН ПОЛНОГО ТОКА один из основных законов электромагнитного поля. Устанавливает взаимосвязь между магнитной силой и величиной тока, проходящего через поверхность. Под полным током понимается алгебраическая сумма токов, пронизывающих поверхность, ограниченную замкнутым контуром.
Намагничивающая сила вдоль контура равна полному току, проходящему сквозь поверхность, ограниченную этим контуром. В общем случае напряженность поля на различных участках магнитной линии может иметь разные значения, и тогда намагничивающая сила будет равна сумме намагничивающих сил каждой линии.
ЗАКОН ЛЕНЦА — основное правило, охватывающее все случаи электромагнитной индукции и позволяющее установить направление возникающей э.д.с. индукции.
Согласно закону Ленца это направление во всех случаях таково, что ток, созданный возникшей э.д.с., препятствует тем изменениям, которые вызвали появление э.д.с. индукции. Этот закон является качественной формулировкой закона сохранения энергии в применении к электромагнитной индукции.
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ, закон Фарадея – закон, устанавливающий взаимосвязь между магнитными и электрическими явлениями. ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром. Величина ЭДС поля зависит от скорости изменения магнитного потока.
ЗАКОНЫ ФАРАДЕЯ (по имени английского физика М.Фарадея (1791-1867)) – основные законы электролиза.
Устанавливают взаимосвязь между количеством электричества, проходящего через электропроводящий раствор (электролит), и количеством вещества, выделяющегося на электродах.
При пропускании через электролит постоянного тока I в течение секунды q = It, m = kIt.
Второй закон ФАРАДЕЯ: электрохимические эквиваленты элементов прямо пропорциональны их химическим эквивалентам.
ПРАВИЛО БУРАВЧИКА — правило, позволяющее определить направление магнитного поля, зависящее от направления электрического тока. При совпадении поступательного движения буравчика с протекающим током направление вращения его рукоятки указывает направление магнитных линий. Или при совпадении направления вращения рукоятки буравчика с направлением тока в контуре поступательное движение буравчика указывает направление магнитных линий, пронизывающих поверхность, ограниченную контуром.
Правило буравчика
ПРАВИЛО ЛЕВОЙ РУКИ — правило, позволяющее определить направление электромагнитной силы. Если ладонь левой руки расположена так, что вектор магнитной индукции входит в нее (вытянутые четыре пальца совпадают с направлением тока), то отогнутый под прямым углом большой палец левой руки показывает направление электромагнитной силы.
Правило левой руки
ПРАВИЛО ПРАВОЙ РУКИ — правило, позволяющее определить направление наведенной эдс электромагнитной индукции. Ладонь правой руки располагают так, чтобы магнитные линии входили в нее. Отогнутый под прямым углом большой палец совмещают с направлением движения проводника. Вытянутые четыре пальца укажут направление индуктированной эдс.
8. Задача анализа и расчета линейных электрических цепей. Общие принципы расчета цепей на примере цепей постоянного тока.
9.ОТВЕТИЛ Понятие эквивалентности. Основные эквивалентные преобразования участка цепи не содержащего источники энергии.
Для упрощения анализа сложных электрических цепей отдельные их участки, не содержащие ЭДС, или пассивные цепи целиком можно заменить одним эквивалентным сопротивлением. Под эквивалентным понимают такое сопротивление, которое, будучи включенным в цепь вместо заменяемой группы сопротивлений, не изменяет распределение токов и напряжений в остальной части цепи.
При последовательном соединении сопротивлений по каждому из них
протекает один тот же ток, следовательно, падение напряжения на эквивалентном сопротивлении должно быть равно сумме падений напряжений на исходных сопротивлениях:
отсюда получаем:
Если группа заменяемых сопротивлений соединена параллельно, то
напряжения на каждом из них и на эквивалентном сопротивлении одинаковы. Условия эквивалентности будут выполнены, если ток через искомое сопротивление будет равен сумме токов через отдельные параллельные сопротивления:
Используя закон Ома для отдельного сопротивления, можем записать:
Окончательно получаем:
Поскольку величина, обратная сопротивлению, есть проводимость, то, вводя обозначения для проводимости , получим:
При анализе сложных схем встречаются случаи, когда часть схемы образует так называемый треугольник сопротивлений:
Схема упрощается, если треугольник с сопротивлениями Rав, Rвс, Rса заменить эквивалентной звездой с сопротивлениями Rа, Rв, Rс. Иногда, наоборот, необходимо обратное преобразование звезды в треугольник. Схемы треугольника и звезды считаются эквивалентными, если после преобразования все токи и напряжения в остальных частях схемы (не затронутых преобразованиями) остаются неизменными.
Очевидно, условия эквивалентности должны выполняться и при обрыве проводов, подходящих к узлам «а», «в», «с». Например, при обрыве провода, подходящего к узлу «а», сопротивления между точками «в» и «с» в треугольнике и звезде должны быть одинаковы, т.е.:
Рассуждая аналогичным образом, можно записать:
Решая полученную систему уравнений относительно Rа, Rв и Rс, получим формулы эквивалентного преобразования треугольника в звезду:
Решая систему относительно и получим формулы преобразования звезды в треугольник:
В частном случае, когда сопротивления звезды или треугольника одинаковы, эти формулы упрощаются:
10.ОТВЕТИЛ Понятие об эквивалентных преобразованиях участка цепи, содержащего источники и приемники энергии.