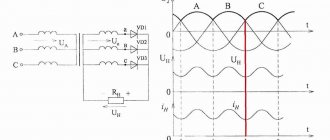
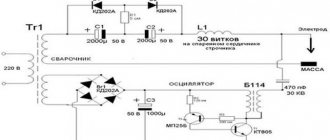
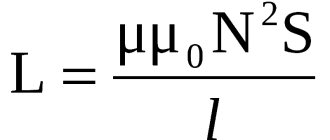Колебательный контур LC
Колебательный контур
— электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.
Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
— Конденсатор C
– реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию. — Катушка индуктивности
L
– реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.
Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC
.
Основные свойства индуктивности
— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией . — Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.
Природа электромагнитных колебаний в контуре
Период свободных колебаний контура LC
можно описать следующим образом:
Если конденсатор ёмкостью C
заряжен до напряжения
U
, потенциальная энергия его заряда составит. Если параллельно заряженному конденсатору подключить катушку индуктивности
L
, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.
Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t
1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта
t
1 = . По истечении времени
t
1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны. Накопленная катушкой магнитная энергия в этот момент составит. В идеальном рассмотрении, при полном отсутствии потерь в контуре,
EC
будет равна
EL
. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.
Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t
2 =
t
1, он перезарядит конденсатор от нулевого до максимального отрицательного значения (
-U
). Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.
Описанные интервалы t
1 и
t
2 составят половину периода полного колебания в контуре. Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени
t
3, сменив полярность полюсов.
В течении заключительного этапа колебания (t
4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения
U
(в случае отсутствия потерь) и процесс колебания повторится.
В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде. Время t
1 +
t
2 +
t
3 +
t
4 составит период колебаний . Частота свободных колебаний контура ƒ = 1 /
T
Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности XL=2πfL
равно реактивному сопротивлению ёмкости
XC=1/(2πfC)
.
Расчёт частоты резонанса LC-контура:
Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.
Необходимо вписать значения и кликнуть мышкой в таблице. При переключении множителей автоматически происходит пересчёт результата.
Наверх
Расчёт частоты:
| Частота резонанса колебательного контура LC. ƒ = 1/(2π√(LC)) |
Расчёт ёмкости:
| Ёмкость для колебательного контура LC C = 1/(4𲃲L) |
Расчёт индуктивности:
| Индуктивность для колебательного контура LC L = 1/(4𲃲C) |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать реактивное сопротивление.
Рассчитать реактивную мощность и компенсацию.
Идеальный колебательный контур. Формула Томсона
На прошлом уроке мы с вами познакомились с электромагнитными колебаниями. Напомним, что так называют периодические изменения со временем электрических и магнитных величин в электрической цепи.
Рассмотрев качественную сторону теории процессов в колебательном контуре, перейдём к её количественной стороне. Для этого рассмотрим идеальный колебательный контур, то есть контур, активное сопротивление которого пренебрежимо мало.
В таком контуре, как мы показали ранее, полная электромагнитная энергия в любой момент времени равна сумме энергий электрического и магнитного полей, и она не меняется с течением времени:
А раз энергия контура неизменная, то производная полной энергии по времени равна нулю:
Напомним, что в записанной формуле заряд и сила тока в цепи являются функцией времени.
Чтобы понять физический смысл этого уравнения, перепишем его так:
Из такой записи видно, что скорость изменения магнитного поля по модулю равна скорости изменения энергии электрического поля.
А знак минус в формуле показывает на то, что увеличение энергии магнитного поля происходит за счёт убыли энергии поля электрического.
Вычислим производные в записанном уравнении, воспользовавшись для этого формулой вычисления производной сложной функции.
А теперь вспомним, что производная заряда по времени есть сила мгновенного тока (то есть сила тока в данный момент времени):
Поэтому предыдущее уравнение можно переписать так, как показано на экране:
Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому, как производная скорости по времени (то есть ускорение) есть вторая производная координаты по времени:
Перепишем предыдущее равенство с учётом этой поправки:
Разделив левую и правую части этого уравнения на «Эль И» (Li
), получим
основное уравнение, описывающее свободные гармонические электрические колебания в контуре:
Данное уравнение аналогично уравнению, описывающему гармонические механические колебания:
Отсюда видно, что величина, обратная квадратному корню из произведения индуктивности и ёмкости, является циклической частотой свободных электрических колебаний:
Зная циклическую частоту колебаний, нетрудно найти и их период, то есть минимальный промежуток времени, через который процесс в колебательном контуре полностью повторяется:
Эта формула впервые была получена английским физиком Уильямом Томсоном 1853 году, и в настоящее время носит его имя.
Из формулы видно, что период колебательного контура определяется параметрами составляющих его элементов: индуктивностью катушки и ёмкостью конденсатора.
Из формулы Томсона также следует, что, например, при уменьшении ёмкости или индуктивности период колебаний должен уменьшиться, а их частота — увеличиться и наоборот.
Но вернёмся к уравнению свободных электромагнитных колебаний в идеальном колебательном контуре. Его решением является уравнение, выражающее зависимость заряда конденсатора от времени:
В записанной формуле qm
— это
начальное (или амплитудное) значение заряда
, сообщённому конденсатору. Из этой формулы следует, что заряд на конденсаторе изменяется со временем по гармоническому закону.
Если взять первую производную заряда конденсатора по времени, то мы получим уравнение, описывающее изменение силы тока в контуре:
Величина, равная произведению максимального заряда конденсатора и циклической частоты колебаний, является амплитудным значением силы тока:
Перепишем уравнение для силы тока с учётом последнего равенства, а также воспользовавшись формулой приведения:
Из такой записи хорошо видно, что сила тока в колебательном контуре также совершает гармонические колебания с той же частотой, но по фазе она смещена на π
/2 относительно колебаний заряда.
Для закрепления материала, решим с вами такую задачу. Конденсатор ёмкостью 2 мкФ зарядили до напряжения 100 В, а затем замкнули на катушку с индуктивностью 5 мГн. Определите заряд конденсатора через 0,025π мс после замыкания.
В заключение отметим, что в реальных колебательных контурах всегда имеется активное сопротивление, поэтому часть энергии контура всегда превращается во внутреннюю проводников, которая выделяется в виде излучения. Кроме того, часть энергии теряется на перемагничивание сердечника и изменение поляризации диэлектрика. Поэтому полная энергия контура с течением времени уменьшается, в результате уменьшается и амплитуда колебаний. Следовательно, реальные электромагнитные колебания в контуре являются затухающими.
Как работает контур колебаний
Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.
Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.
Вам это будет интересно Описание кабеля КСПВ
Процессы в системе
Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников.
Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.
Осциллограмма
При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.
Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.
Зависимость предельной частоты от добротности
Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот.
Работа электрического колебательного контура
Рис.9. Схема резонансного контура без активного сопротивления в цепи с ёмкостью.
Важной особенностью резонанса токов в параллельном колебательном контуре является то, что реактивные составляющие токов параллельных ветвей компенсируют друг друга, а токи в этих ветвях обычно значительно превышают ток в неразветвлённой части (общая цепь сети), то этот электрический резонанс и назван резонансом токов.
Вывод. Токи в параллельных ветвях резонансного контура I1 и I2 (смотри рис.6) при резонансе токов порознь во столько раз больше тока I0 неразветвлённого участка контура, во сколько раз волновое сопротивление контура ρ = √L/C, больше его активного сопротивления r.
Добротность или качество контура Q = ρ/r1 (рис.9). И тогда добротность контура – это величина, показывающая, во сколько раз ток в резонаторе (резонансный контур) больше тока неразветвлённой части цепи при резонансе токов. I1/I = I2/I = Q (рис.6). Качество резонаторов достигает большой величины (1 000 и более), поэтому важно знать условие резонанса токов в параллельном контуре.
В этом одно из важнейших свойства структуры памяти – резонансное узнавание информации и быстрота мышления.
В отличие от резонанса напряжений (в чувствительных системах) при резонансе токов в структуре памяти сумма энергий электрического и магнитного полей контура памяти не является величиной постоянной. Это означает, что имеются такие моменты, когда электрическая или магнитная энергия полей контура расходуются частично или полностью в активном сопротивлении контура памяти.
Имеются и такие промежутки времени, когда источник энергии питания памяти -чувствительная система -пополняет запас энергии, израсходованный электрическим и магнитным полями контура. Однако обмена реактивной энергией между чувствительной системой и магнитной энергией структуры памяти в параллельном контуре не происходит. Последовательный колебательный контур чувствительной системы в общей сложности за один период колебаний доставляет в контур памяти такое количество энергии, которое было израсходовано в активном сопротивлении контура – на нагревание при мышлении и на излучение электромагнитных волн мыслей.
Удивительно то, что работа головного мозга человека, обеспечиваемая ретикулярной формацией продолговатого мозга как источником электрического поля, до деталей в точности тождественна работе технического параллельного колебательного контура при резонансе токов[2].
В реальности каждый человек ощущает это явление каждую ночь в режиме так называемого быстрого (или парадоксального) сна. Нейроны мозга в режиме отдыха тела (при отключении органов ощущения) питаются энергией ретикулярной формации. А в режиме бодрствования органы ощущения напрямую подзаряжают ретикулярную систему, и так повторяется всю жизнь. Мозг не может мыслить без энергии, ретикулярная формация не может сама вырабатывать электрическую энергию, ей нужна система чувствования, способная взаимодействовать с электромагнитной средой, преобразовывая излучения в токи той же частоты, свойственной данному виду живых существ. Поэтому в природе существует главный закон – закон сохранения и развития жизни, осуществляемый через процесс познания законов природы и сохранения этих знаний.
В заключении рассмотрим,как изменяются реактивные токи: I1 в параллельной ветви с индуктивностью; I2 в параллельной ветви с ёмкостью; и общий ток I в неразветвлённой цепи колебательного контура в зависимости от частоты вынужденных колебаний ω. Рассмотрим это для реального случая, когда активное сопротивление спиральной структуры памяти мало, а в цепи накопителя энергии оно вообще равно нулю (рис. 10).
I1 = U /ω0 L;
I2 = U / (1 / ω0 C) = U ω0 C.
Рис. 10. График изменения токов I1; I2 в параллельных ветвях колебательного контура и общего тока Iв зависимости от угловой частоты ω.
Ток в параллельной ветви с индуктивностьюI1 (а это ток элемента памяти) изменяется в зависимости от частоты вынужденных колебаний по гиперболическому закону. При ω = 0 ток в этом участке равен отношению напряжения к малой величине активного сопротивления в индуктивной цепи. А при ω → ∞ ток I1 стремится к нулю.
Это означает, что ток в структуре памяти I1 с ростом частоты вынужденных колебаний уменьшается до полного прекращения. Поэтому-то высокочастотные колебания, поступающие из внешней среды, вредны для структуры памяти – она прекращает мыслить. С ростом частоты внешних сигналов память перестаёт реагировать на них, она не различает их изменения, не развивается и полностью от них отключается.
У чувствительных систем с ёмкостными свойствами, наоборот, с ростом частоты вынужденных колебаний внешней среды растут токи I2 до бесконечности, что гибельно для самих элементов. При малой частоте колебаний внешней волны рецепторы не воспринимают эту волну, они теряют бдительность, не замечая изменений.
Это также говорит о том, что чувствительная система начинает своё развитие с высокочастотных сигналов, постепенно переходя к более низким частотам. Книга жизни читается с начала, а не с конца, путём логического считывания информации с нарастанием её смысла, т.е. с нарастанием длины волны.
Когда в поведении людей отмечается быстрота разговорной речи, следует видеть конец их эволюции.
Как зависит течение токов в параллельном колебательном контуре, особенно в индуктивной его части, при неизменной частоте напряжения, идущего от чувствительной системы, но при этом изменяется величина электрической ёмкости? Другими словами, как реагирует структура памяти на величину электрической ёмкости её источника питания в условиях неизменной сигнальной информации среды? Ход изменения токов представлен на рис. 11.
Рис. 11. График изменения токов в структуре памяти (в виде параллельного колебательного контура) в зависимости от изменения электрической ёмкости от нуля до бесконечности.
Ток в индуктивном элементе памяти I1 = U /ω0L
не зависит от величины электрической ёмкости (от размеров источника питания) в параллельно ветви контура при постоянстве действующего напряжения вынужденных колебаний со стороны чувствительной системы.
Ток в ёмкостной цепи I2 растёт с ростом величины самой ёмкости: I2 = UωC. При этом структура самой памяти не берёт тока больше, чем это ей надо. Сама природа показывает, что элита от природы даже при нарастании всяческих благ, нарастании жизненной энергии (источников питания) не берёт для себя излишеств, довольствуясь номинальной потребностью. Общая потребительская корзина I (рис.11) сначала падает до оптимального уровня роста источника питания C0, а потом стремительно нарастает. А разум говорит, что ему не требуется больше того, что необходимо. Потребительский спрос растёт там, где мало ума, нет опыта жизни, чем больше имеют, тем больше хочется иметь.
Мыслит или не мыслит каждая форма вещества? Косвенным доказательством мышления у каждой формы вещества служит наличие частоты собственных незатухающих колебаний,наличие собственного источника энергии питания у каждой структуры памяти. Затраты энергии на мышление компенсируются энергией источника питания. Если есть источник питания, значит,форма вещества мыслит, какой бы малой она ни была!
Непрерывная мысль состоит из дискретных её единиц. Наименьшей формой вещества, обладающей наименьшей порцией мысли, является универсальная форма дейтерия – соединение последовательной колебательной структуры атома водорода и параллельной колеблющейся структуры нейтрона (универсальный элементарный квадруполь). Атомы химических элементов представляют собой отдельные «буквы общей Азбуки»жизни, из них слагаются слоги, слова, предложения, тексты, течёт мысль, воплощаясь в формы материи.
Вывод
Поскольку все формы вещества и излучений имеют одну и ту же электромагнитную природу происхождения, то все они являются колебательными системами. Все внутренние процессы в колебательной системе, состоящей из структуры памяти (индуктивности) и чувствительной оболочки (рецепторы с электрическими свойствами) являются электромагнитными. Поэтому делаем вывод: жизнь имеет электромагнитное происхождение.
Рис. 12. Эквивалентная схема живой вещественной системы.
Последовательный колебательный контур L1 C1 — чувствительная система и параллельный колебательный контур L2 C2 – образуют единое целое, живую структурную форма вещества.
Два Начала, одно с магнитными свойствами индуктивности, а другое с электрическими свойствами,образуют целостную структуру, готовую к ритму колебательного процесса. Готовую, но ещё не колеблющуюся.
Данная система возбуждается, в полном смысле слова – оживает, с приходом в область её пребывания электромагнитной волны соответствующего диапазона частот. Порция энергии волны вдохнула жизнь в данную форму, и в ней возникает волнообразный процесс перекачки энергии от электрической ёмкости к индуктивной спиральной форме памяти и обратно от индуктивности к ёмкости без участия внешнего поля волны. Началась самостоятельная жизнь данной формы вещества, и этот колебательный процесс может длиться долго.
Но внешняя волна пришла снова, и своим напряжением возбудила чувствительные элементы последовательного колебательного контура, за счёт чего слабое напряжение волны усилилось в сотни тысяч раз. И усиленное напряжение без искажения смысла передаётся в параллельную структуру колебательного контура, где вызывает токи, текущие по замкнутому контуру в режиме незатухающих колебаний. Так напряжение внешней волны преобразовывается в токи структуры памяти, и хранится в неизменном виде незатухающих колебаний. Движение токов формирует магнитное поле той же формы, что и токоведущая система. Так формируется форма мысли за пределами контура токов.
Потери энергии за счёт мышления требуют компенсации от своего источника энергии, которому в свою очередь требуется подзарядка от чувствительной системы, а рецепторам нужно наличие внешнего электромагнитного поля, которое формируется генетическим центром следующего уровня иерархии форм. Так возбуждается жизнь, возникает рост и развитие под внешним управлением до уровня совершенствования, заданного геномом внешней среды.
Назначением каждой формы вещества является поддержание своих внутренних колебаний в заданном диапазоне параметров. Если в среде заметна убыль ЭМИ данного уровня, одиночные родственные элементы объединяются на том же принципе диполей, так формируются системы, способные воспринимать ЭМИ длинных волн и расщеплять их до нужного предела. Начался живой процесс. Так форма материи становится МЕРОЙ информационного содержания во внешнем электромагнитном поле
Контрольные вопросы к уроку №8
1.Почему Жизнь имеет электромагнитное происхождение?
2.В чём проявляется универсальность колебательной системы?
3.В чём разница параллельного и последовательного колебательного контура?
4.Расскажите процесс зарядки и разряда конденсатора.
5.Что такое индуктивность, самоиндукция, индукция?
6.Что препятствует быстрому заряду и разряду источника питания структуры памяти?
7.Как связано существование магнитного поля с динамикой электрических зарядов?
8.Что такое круговая частота и частота собственных незатухающих колебаний? Связь частоты и длины волны излучений через скорость света. Связь частоты колебаний со временем и пространством.
9.Что такое резонанс напряжений, где он возникает, и что он даёт?
10.Почему все чувствительные органы работают в напряжённом режиме?
11.Что служит причиной приёма и обработки электромагнитной информации без искажения во внутрь живой системы?
12.Чем объяснить индивидуальное существование взаимозависимых элементов в системе тел и систем между собой?
13.Что такое резонанс токов и кому он принадлежит?
14.Чем можно объяснить сверхслабые взаимодействия в биологии и медицине?
15.Расскажите суть БЫСТРОГО или парадоксального сна у всех млекопитающих? У кого он может ещё быть?
Нужен ли источник электрической энергии для структуры памяти? Роль белковых молекул для генома – ДНК.
[1] Индуктивность – иначе называется как коэффициент самоиндукции, количественная характеристика связи между силой электрического тока в замкнутом контуре с магнитным потоком через контур, созданным током в контуре.
Магнитная индукция – мера магнитного состояния магнитного поля, величина векторная.
[2] Цыган В.Н., Богославский М.М.,Князькин И.В., Апчел В.Я. Физиология и патология сна. СПб.: ВМА. Специальная литература. 2006. – 160с.
Урок №8. Презентация Microsoft PowerPoint.ppt
Начинающим о колебательном контуре
Для начинающих радиолюбителей хотелось бы привести немного информации о параметрах колебательных контуров. Ведь катушки индуктивности в основном являются их составной частью. Контур, как известно, состоит из катушки индуктивности и конденсатора. Рассмотрим параллельный контур, как наиболее часто встречающиийся.
Основными характеристиками контура являются:
- Резонансная частота контура
- Добротность контура
- Эквивалентное сопротивление контура
- Полоса пропускания
Рис1.
Резонансная частота контура определяется по формуле:
| Где L и C в Генри и Фарадах соответственно. |
Однако, необходимо помнить об одном очень важном моменте. C — это не номинальная емкость конденсатора контура. Она слагается из суммы емкостей — этого конденсатора, паразитной емкости катушки, емкости внешних цепей, подключенных к контуру (например выходная и входная емкость транзисторного каскада), паразитной емкости монтажа. Эти привнесенные емкости имеют достаточно существенную величину, особенно на высоких частотах, где они соизмеримы с емкостью самого контурного конденсатора. Их необходимо учитывать! Иногда на форумах можно прочесть сообщения типа: » Я рассчитал катушку, пользуясь такой-то программой, собрал конструкцию, а потом оказалось, что витки пришлось подбирать методом » научного тыка «, зачем такая программа, если она неправильно считает «. Программа считает правильно. Просто она считает «голый» контур, а на схему и конструкцию устройства надо, как говорил персонаж известного фильма, смотреть «ширше и глубже».
Теоретически, все вышесказанное относится и к индуктивности L, однако в реальности, привнесенные в контур индуктивности на порядок меньше и их в большинстве случаев можно не учитывать.
Добротность «голого» ненагруженного контура Q определяется добротностями катушки QL и конденсатора QC. QLзависит от сопротивления rL (см. рис1.), эквивалентного потерям электрической энергии в проводе, в изоляции провода, каркасе, экране, сердечнике катушки индуктивности. QL = 2πƒL /rL. Обычно в зависимости от качества конструкции катушки индуктивности и применяемых материалов QL≈50÷250.
Добротность конденсатора QC Зависит от сопротивления RC, эквивалентного потерям диалектической энергии в конденсаторе. QC = 1/(2πƒСRC). Обычно QC≈400÷1000.
Всевозможные сопротивления потерь (rL,RC) можно, для удобства расчетов заменить одним сопротивлением Rэ, подключенным параллельно идеальному контуру без потерь, которое называется эквивалентным сопротивлением контура. Оно характеризует все потери реального контура и равно сопротивлению контура на резонансной частоте. Попутно замечу, что на резонансной частоте реактивные сопротивления катушки и конденсатора равны и противоположны по знаку и компенсируют друг друга, в результате общее сопротивление контура чисто активно. Величина Rэ связана с другими параметрами контура следующими соотношениями: Rэ = 2πf0LQ = Q/(2πf0C) , f0 – резонансная частота.
Здесь опять существует важный момент. При подключении к контуру внешних цепей параллельно Rэ подключаются дополнительные сопротивления, вносимые внешними цепями. При этом Rэ и Q уменьшаются. Причем для высокодобротных контуров, это уменьшение может быть существенным. Чтобы минимизировать влияние внешних цепей на контур, применяют частичное включение через емкостный делитель, отвод катушки, либо применяют катушку связи.
Полоса пропускания равна полосе частот, где коэффициент передачи контура равен 70,7% от коэффициента передачи на резонансной частоте.
Справедливо соотношение: Q = f/Δf , которое можно использовать для измерения добротности реального контура.
Имеет какое-либо значение отношение индуктивности к емкости конденсатора? Как выбрать оптимальное? Колебательный контур характеризуется параметром ρ = √L/C, называемым характеристическим сопротивлением. Этот параметр и ,соответственно, оптимальное соотношение L/C, зависят от импедансов схемы в которую включен колебательный контур. Ориентировочно в транзисторных схемах ρ ≈ 500-2000 ом на частотах КВ и 70-200 ом на частотах УКВ. С ростом частоты ρ стараются понижать для уменьшения влияния наводок и паразитных емкостей схемы и для избежания самовозбуждения.
Подводя итог, отмечу, что колебательный контур широко используется в радиотехнических устройствах для фильтрации электрических колебаний, для поворота фазы, для согласования сопротивлений и для других целей. При расчете контура обязательно необходимо учитывать параметры внешних цепей, подключенных к контуру и качественные характеристики самих деталей контура, особенно катушки индуктивности.
Что такое колебательный контур
Колебательный контур это несколько элементов в любой электрической цепи, емкость и индуктивность, которых соединены параллельно или последовательно. Для нормального функционирования колебательного контура в цепи необходим источник энергии.
Параллельный контур колебаний
При параллельном или последовательном соединениях элементов, входящих в состав электрической цепи, та или иная замкнутая проводниковая система получает одноимённое название. Явление резонанса в обоих случаях, возникает аналогичным образом, только в случае параллельного колебательного контура этот показатель относится к силе тока, а в случае с последовательным – возникает предельная частотность мгновенного изменения напряжений.
Формула индуктивности
Расчет резонанса колебательного контура производится на основании значений емкости и индуктивности. Как правило, емкость конденсатора является постоянной величиной, за исключением случаев использования переменных устройств в перестраиваемых электроцепях. Коэффициент самоиндукции катушки зависит от многих факторов:
- Количество и расположение витков обмотки;
- Наличие или отсутствие сердечника;
- Материал сердечника.
Общей формулы для определения индуктивности катушки колебательного контура не существует. Для расчетов используют формулы, соответствующие форме катушки. К сожалению, все формулы определения качественной величины электрической цепи с подсоединённой к ней катушкой индуктивности позволяют производить только приблизительные расчеты.
Вам это будет интересно Особенности кабеля Frls
Приборы индуктивности различных типов
Важно! Для того, чтобы получить катушку с заданными параметрами, приходится принимать дополнительные меры, например, производить подстройку коэффициента самоиндукции путем изменения длины сердечника или корректировки расстояния между витками в однорядных катушках.