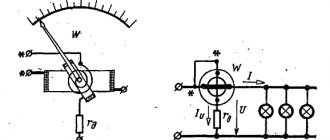
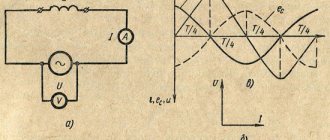
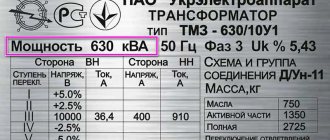
Переменный ток — электрический ток, направление и сила которого изменяются периодически. Так как обычно сила переменного тока изменяется по синусоидальному закону, то переменный ток представляет собой синусоидальные колебания напряжения и силы тока.
Поэтому к переменному току применимо все то, что относится к синусоидальным электрическим колебаниям. Синусоидальные колебания — колебания, при которых колеблющаяся величина изменяется по закону синуса. В данной статье поговорим о параметрах переменного тока.
Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами:
Есть и вспомогательные параметры:
Далее рассмотрим все эти параметры по отдельности и во взаимосвязи.
Период — время, в течение которого система, совершающая колебания, проходит через все промежуточные состояния и нале снова возвращается к исходному.
Периодом Т переменного тока называется промежуток времени, за который ток или напряжение совершает один полный цикл изменений.
Поскольку источником переменного тока является генератор, то период связан со скоростью вращения его ротора, и чем выше скорость вращения витка или ротора генератора, тем меньшим оказывается период генерируемой переменной ЭДС, и, соответственно, переменного тока нагрузки.
Период измеряется в секундах, миллисекундах, микросекундах, наносекундах, в зависимости от конкретной ситуации, в которой данный ток рассматривается. На вышеприведенном рисунке видно, как напряжение U с течением времени изменяется, имея при этом постоянный характерный период Т.
Частота f является величиной обратной периоду, и численно равна количеству периодов изменения тока или ЭДС за 1 секунду. То есть f = 1/Т. Единица измерения частоты — герц (Гц), названная в честь немецкого физика Генриха Герца, внесшего в 19 веке немалый вклад в развитие электродинамики. Чем меньше период, тем выше частота изменения ЭДС или тока.
Сегодня в России стандартной частотой переменного тока в электрических сетях является 50 Гц, то есть за 1 секунду происходит 50 колебаний сетевого напряжения.
В других областях электродинамики используются и более высокие частоты, например 20 кГц и более — в современных инверторах, и до единиц МГц в более узких сферах электродинамики. На приведенном выше рисунке видно, что за одну секунду происходит 50 полных колебаний, каждое из которых длится 0,02 секунды, и 1/0,02 = 50.
По графикам изменения синусоидального переменного тока с течением времени видно, что токи различной частоты содержат разное количество периодов на одном и том же отрезке времени.
Угловая частота — число колебаний, совершаемых за 2пи сек.
За один период фаза синусоидальной ЭДС или синусоидального тока изменяется на 2пи радиан или на 360°, поэтому угловая частота переменного синусоидального тока равна:
Пользоваться числом колебаний на 2пи сек. (а не за 1 сек.) удобно потому, что в формулах, выражающих закон изменения напряжений и токов при гармонических колебаниях, выражающих индуктивное или емкостное сопротивление переменному току, и во многих других случаях частота колебаний n фигурируют вместе с множителем 2пи.
Фаза — состояние, стадия периодическою процесса. Более определенный смысл имеет понятие фаза в случае синусоидальных колебаний. На практике обычно играет роль не фаза сама по себе, а сдвиг фаз между какими-либо двумя периодическими процессами.
В данном случае под термином «фаза» понимают стадию развития процесса, и в данном случае, применительно к переменным токам и напряжениям синусоидальной формы, фазой называют состояние переменного тока в определенный момент времени.
На рисунках можно видеть: совпадение напряжения U1 и тока I1 по фазе, напряжения U1 и U2 в противофазе, а также сдвиг по фазе между током I1 и напряжением U2. Сдвиг по фазе измеряется в радианах, долях периода, в градусах.
Амплитуда Uм и Iм
Говоря о величине синусоидального переменного тока или синусоидальной переменной ЭДС, наибольшее значение ЭДС или тока называют амплитудой или амплитудным (максимальным) значением.
Амплитуда
— наибольшее значение величины, совершающей гармонические колебания (например, максимальное значение силы тока в переменном токе, отклонение колеблющегося маятника от положения равновесия), наибольшее отклонение колеблющейся величины от некоторого значения, условно принятого за начальное нулевое.
Переменный электрический ток
Переменный электрический ток
(AC, аббревиатрура от англ. alternating current) — это меняющийся по своей величине и направлению с определенной периодичностью электрический ток. В электротехнике в качестве буквенного обозначения электрического тока принято использовать знак тильда (
Источниками переменного электрического тока служат генераторы переменного тока, создающие переменную электродвижущую силу, изменение величины и направления которой происходит через определенные промежутки времени.
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10 -3 сек.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Основные параметры переменного тока
При подключении к источнику переменного тока с синусоидально изменяющейся э. д. с. электрических цепей с линейными сопротивлениями в них будут действовать синусоидально изменяющиеся напряжения и проходить синусоидально изменяющиеся токи. Переменные токи, э. д. с. и напряжения характеризуются четырьмя основными параметрами: периодом, частотой, амплитудой и действующим значением.
Период.Промежуток времени , в течение которого э. д. с, напряжение и или ток совершают полный цикл изменений, называется периодом. Чем быстрее вращается виток или ротор генератора переменного тока, тем меньше период изменения э. д. с. или тока.
Частота.Число полных периодов изменения э. д. с, напряжения или тока в 1 с называется частотой,
f = 1 / T
Она измеряется в герцах (Гц), т. е. числом периодов в секунду. Чем больше частота, тем меньше период изменения тока, напряжения или э. д. с. . В Советском Союзе все электрические станции переменного тока вырабатывают ток, изменяющийся с частотой 50 Гц, т. е. 50 периодов в секунду. В автоматике и радиотехнике применяют электрические токи и более высоких частот. Такие частоты измеряются в килогерцах (1 кГц=10 3 Гц) и мегагерцах (1 МГц=10 6 Гц).
Амплитуда.Наибольшее значение переменного тока (переменных э. д. с. и напряжения) называют амплитудным значением, или амплитудой.
Действующее значение. Ток, напряжение и э. д. с, действующие в электрической цепи в каждый отдельный момент времени, определяются так называемыми мгновенными значениями.Однако судить о переменных э. д. с, токе или напряжении по их мгновенным значениям неудобно, так как эти значения непрерывно меняются. Поэтому оценивать способность переменного тока совершать механическую работу или создавать тепло принято по действующему его значению. Под действующим значением переменного тока понимают силу такого постоянного тока , который, проходя по проводнику в течение некоторого времени, выделит в нем такое же количество тепла, как и данный переменный ток
.Действующие значения тока, напряжения и э. д. с. обозначают соответственно I, U, Е.
19.Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока.
Иначе говоря, действующее значение тока можно определить по формуле:
.
Для гармонических колебаний тока
Аналогичным образом определяются действующие значения ЭДС и напряжения.
21. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением
.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
Рассмотрим цепь переменного тока (рис. 53), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в Цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в Цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (j=0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
24.
| Емкостное сопротивление в цепи переменного тока |
| При включении конденсатора в цепь постоянного напряжения сила тока I=0, а при включении конденсатора в цепь переменного напряжения сила тока I ? 0. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока. |
| Мгновенное значение напряжения равно . Мгновенное значение силы тока равно: Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2. |
| Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: , где — емкостное сопротивление. |
| Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты). |
| Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току). |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной. |
| 22. Индуктивное сопротивление в цепи переменного тока |
| В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения. |
| Мгновенное значение силы тока: |
| Мгновенное значение напряжения можно установить, учитывая, что u = — εi, где u – мгновенное значение напряжения, а εi – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению. |
| . Следовательно , где амплитуда напряжения. Напряжение опережает ток по фазе на π/2. |
| Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой. |
| Величина — индуктивное сопротивление. |
| Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления. |
| В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка. |
| Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной. |
25. Резонанс напряжений — резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Пусть имеется колебательный контур с частотой собственных колебаний f
, и пусть внутри него работает генератор переменного тока такой же частоты
f
.
В начальный момент конденсатор контура разряжен, генератор не работает. После включения напряжение на генераторе начинает возрастать, заряжая конденсатор. Катушка в первое мгновение не пропускает ток из-за ЭДС самоиндукции. Напряжение на генераторе достигает максимума, заряжая до такого же напряжения конденсатор.
Далее: конденсатор начинает разряжаться на катушку. Напряжение на нем падает с такой же скоростью, с какой уменьшается напряжение на генераторе.
Далее: конденсатор разряжен до нуля, вся энергия электрического поля, имевшаяся в конденсаторе, перешла в энергию магнитного поля катушки. На клеммах генератора в этот момент напряжение нулевое.
Далее: так как магнитное поле не может существовать стационарно, оно начинает уменьшаться, пересекая витки катушки в обратном направлении. На выводах катушки появляется ЭДС индукции, которое начинает перезаряжать конденсатор. В цепи колебательного контура течет ток, только уже противоположно току заряда, так как витки пересекаются полем в обратном направлении. Обкладки конденсатора перезаряжаются зарядами, противоположными первоначальным. Одновременно растет напряжение на генераторе противоположного знака, причем с той же скоростью, с какой катушка заряжает конденсатор.)
Далее: катушка перезарядила конденсатор до максимального напряжения. Напряжение на генераторе к этому моменту тоже достигло максимального.
Возникла следующая ситуация. Конденсатор и генератор соединены последовательно и на обоих напряжение, равное напряжению генератора. При последовательном соединении источников питания их напряжения складываются.
Следовательно, в следующем полупериоде на катушку пойдет удвоенное напряжение (и от генератора, и от конденсатора), и колебания в контуре будут происходить при удвоенном напряжении на катушке.
В контурах с низкой добротностью напряжение на катушке будет ниже удвоенного, так как часть энергии будет рассеиваться (на излучение, на нагрев) и энергия конденсатора не перейдет полностью в энергию катушки). Соединены как бы последовательно генератор и часть конденсатора.
27. Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Численно коэффициент мощности равен косинусу этого фазового сдвига.
Можно показать, что если источник синусоидального тока (например, розетка
220 В, 50 Гц) нагрузить на нагрузку, в которой ток опережает или отстаёт по фазе на некоторый угол от напряжения, то на внутреннем активном сопротивлении источника выделяется повышенная мощность. На практике это означает, что при работе на нагрузку со сдвинутыми напряжением и током от электростанции требуется больше энергии; избыток передаваемой энергии выделяется в виде тепла в проводах и может быть довольно значительным.
Равен отношению потребляемой электроприёмником активной мощности к полной мощности. Активная мощностьрасходуется на совершение работы. Полная мощность — геометрическая сумма активной и реактивной мощностей (в случае синусоидальных тока и напряжения). В общем случае полную мощность можно определить как произведение действующих (среднеквадратических) значений тока и напряжения в цепи. Полная мощность равна корню квадратному из суммы квадратов активной и неактивной мощностей. В качестве единицы измерения полной мощности принято использовать вольт-ампер (В∙А) вместо ватта (Вт).
Согласно неравенству Коши—Буняковского, активная мощность, равная среднему значению произведения тока и напряжения, всегда не превышает произведение соответствующих среднеквадратических значений. Поэтому коэффициент мощности принимает значения от нуля до единицы (то есть от 0 до 100 %).
Коэффициент мощности математически можно интерпретировать как косинус угла между векторами тока и напряжения. Поэтому в случае синусоидальных напряжения и тока величина коэффициента мощности совпадает с косинусом угла, на который отстают соответствующие фазы.
В электроэнергетике для коэффициента мощности приняты обозначения cos φ (где φ — сдвиг фаз между силой токаи напряжением) либо λ. Когда для обозначения коэффициента мощности используется λ, его величину обычно выражают в процентах.
При наличии реактивной составляющей в нагрузке кроме значения коэффициента мощности иногда также указывают характер нагрузки: активно-ёмкостный или активно-индуктивный. В этом случае коэффициент мощности соответственно называют опережающим или отстающим.
В случае синусоидального напряжения, если нагрузка не имеет реактивной составляющей, коэффициент мощности равен доле мощности первой гармоники тока в полной мощности, потребляемой нагрузкой, и равен коэффициенту искажений тока.
Источник
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
.
Рисунок 2. Радиан.
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2
). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
? = 6,28*f = 2f
ПЕРЕМЕННЫЙ ТОК. ОСНОВНЫЕ ПАРАМЕТРЫ
Переменным токомназывают такой электрический ток, который периодически изменяется по величине и направлению.
Для получения переменного тока используют электромашинные генераторы, работа которых основана на явлении электромагнитной индукции. Переменный ток имеет огромное практическое значение. Почти вся электроэнергия вырабатывается в виде энергии переменного тока.
Возможность получать переменный ток различного напряжения (высокого — для передачи энергии на большие расстояния, низкого — для питания различных потребителей), простота устройства генераторов и двигателей переменного тока, надежность их работы, удобство эксплуатации и высокие технические характеристики
дали им широкое применение.
Наибольшее распространение получил синусоидальный ток. Изменение тока по синусоидальному закону происходит плавно, без скачков и резких перепадов, что благоприятно сказывается на работе электрических машин и аппаратов.
Временная диаграмма синусоидального тока приведена на рис.1. Его мгновенное значение описывается формулой
Где
— максимальное значение (амплитуда) тока; — угловая частота; — начальная фаза (значение аргумента в начальный момент времени, т. е. при t = 0).
Переменная ЭДС, переменное напряжение и переменный ток характеризуются периодом, частотой, мгновенным, максимальны значениями, действующей величиной.
Рис. .1. Временная диаграмма синусоидального тока
Период. Время, в течение которого переменная ЭДС (напряжение или ток) совершает одно полное изменение по величине и направлению (один цикл), называется периодом. Период обозначается буквой T и измеряется в секундах (с).
Частота. Число полных изменений переменной ЭДС (напряжения или тока),совершаемых за 1 с, называется частотой. Частота обозначается буквой
и измеряется в герцах (Гц). При измерении больших частот пользуются единицами килогерц (кГц) и мегагерц (МГц):
1 кГц = 1 ООО Гц, 1 МГц = 1 ООО кГц = 1 ООО ООО Гц.
Чем больше частота переменного тока, тем короче период. Таким образом, частота — это величина, обратная периоду:
При вращении витка в магнитном поле один его оборот соответствует 360°, или 2л радиан. Угловая скорость вращения этого витка выражается в радианах в секунду (рад/с) и определяется отношением
. Эта величина называется угловой частотой и обозначается буквой :
Угловая частота тока
выраженная в радианах в секунду,больше частоты тока выраженной в герцах в раз
Мгновенное и максимальное значения. Величины переменной ЭДС, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин, обозначают соответственно строчными буквами (,
, , ) и записывают следующим образом:
Максимальным значением (амплитудой) переменной ЭДС (напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается
, напряжения —
Um, тока —
Действующая величина. Действующим значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменый ток, выделяет одинаковое количество теплоты
Источник
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник
Синусоидальный ток и основные характеризующие его величины.
Синусоидальный ток и основные характеризующие его величины.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):
(3.1)
Максимальное значение функции называют амплитудой.
Амплитуду тока обозначают
Im.
Период Т
— это время, за которое совершается одно полное колебание.
Рисунок 3.1
Частота f —
число колебаний в 1 с (единица частоты
f —
герц (Гц) или с-1):
(3.2)
Угловая частота (единица угловой частоты — рад/с или с-1)
(3.3)
Аргумент синуса, т. е. ( t
+ ), называют
фазой —
характеризует состояние колебания (числовое значение) в данный момент времени
t
.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью различных полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ).
Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их
е
и
j
(или
e(t)
и
j
(
t
)).
Среднее и действующее значения синусоидально изменяющейся величины.
Под средним значением
синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока
(3.4)
т. е. среднее значение синусоидального тока составляет 2/ = 0,638 от амплитудного. Аналогично,
Eср = 2Em/ ; Uср = 2Um/ .
Широко применяют понятие действующего значения
синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока
(3.5)
Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично
Действующее значение синусоидального тока I
численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.
Большинство измерительных приборов показывают действующее значение измеряемой величины.
Коэффициент амплитуды кa —
это отношение амплитуды периодически изменяющейся функции к ее действующему значению. Для синусоидального тока
(3.6)
Под коэффициентом формы кф —понимают отношение действующего значения периодически изменяющейся функции к ее среднему за полпериода значению. Для синусоидального тока
(3.7)
Сложение и вычитание синусоидальных функций времени на комплексной плоскости. Векторная диаграмма.
Положим, что необходимо сложить два тока (i1
и
i2
) одинаковой частоты. Сумма их дает некоторый ток той же частоты:
Требуется найти амплитуду Iт
и начальную фазу
ψ
тока
i
. С этой целью ток
i1
изобразим на комплексной плоскости (рис. 3.4) вектором =
I1теjψ1
, а ток
i2
— вектором =
I2теjψ2.
Геометрическая сумма векторов и
I2т
даст комплексную амплитуду суммарного тока
Iт = Iт
e-jψ2 . Амплитуда тока
Iт
определяется длиной суммарного вектора, а начальная фаза
ψ
— углом, образованным этим вектором и осью + 1.
Рисунок 3.4
Для определения разности двух токов (ЭДС, напряжений) следует на комплексной плоскости произвести не сложение, а вычитание соответствующих векторов.
Обратим внимание на то, что если бы векторы , ,Iт
стали вращаться вокруг начала координат с угловой скоростью ω, то взаимное расположение векторов относительно друг друга осталось бы без изменений.
Векторной диаграммойназывают совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением правильной ориентации их относительно друг друга по фазе. Пример на рис. 3.4.
Мгновенная мощность.
Протекание синусоидальных токов по участкам электрической цепи сопровождается потреблением энергии от источников. Скорость поступления энергии характеризуется мощностью. Под мгновенным значением мощности, или под мгновенной мощностью,
понимают произведение мгновенного значения напряжения
и
на участке цепи на мгновенное значение тока
i
, протекающего по этому участку:
(3.14)
где р —
функция времени.
Перед тем как приступить к изучению основ расчета сложных цепей синусоидального тока, рассмотрим соотношения между токами и напряжениями в простейших цепях, векторные диаграммы для них и кривые мгновенных значений различных величин. Элементами реальных цепей синусоидального тока являются резисторы, индуктивные катушки и конденсаторы. Протеканию синусоидального тока оказывают сопротивление резистивные элементы (резисторы) — в них выделяется энергия в виде теплоты — и реактивные элементы (индуктивные катушки и конденсаторы) — они то запасают энергию в магнитном (электрическом) поле, то отдают ее. Рассмотрим поведение этих элементов.
Комплексная проводимость.
Под комплексной проводимостью Y
понимают величину, обратную комплексному сопротивлению Z:
(3.37)
Единица комплексной проводимости — См (Ом-1). Действительную часть ее обозначают через g,
мнимую — через
b.
Так как
то
(3.38)
Если X
положительно, то и
b
положительно. При
X
отрицательном
b
также отрицательно.
При использовании комплексной проводимости закон Ома (3.35) запи-сывают так:
(3.39)
или
где Ia
— активная составляющая тока;
Ir —
реактивная составляющая ; тока;
U —
напряжение на участке цепи, сопротивление которого равно Z.
Определение дуальной цепи.
Две электрические цепи называют дуальными,
если закон изменения контурных токов в одной из них подобен закону изменения узловых потенциалов в другой. Исходную и дуальную ей схемы называют
взаимно обратными.
В качестве простейшего примера на рис. 3.32изображены две дуальные цепи.
Рис.3.32.
Схема на рис. 3.32, а
состоит из источника ЭДС
Е
и последовательно с ним включенных активного, индуктивного и емкостного элементов (
R, L, С).
Схема на рис. 3.32
б
состоит из источника тока
J3
и трех параллельных ветвей. Первая ветвь содержит активную проводимость
gэ
вторая — емкость
Сэ,
третья — индуктивность
Zэ
.
Для того чтобы показать, какого рода соответствие имеет место в дуальных цепях, составим для схемы на рис. 3.32, а
уравнение по методу контурных токов:
(3.85)
а для схемы на рис. 3.32б —
по методу узловых потенциалов, обозначив потенциал точки
а
через φа, положив равным нулю потенциал второго узла:
(3.86)
Если параметры gэ, Lэ. Сэ
, схемы (рис. 3.32
б)
согласовать с параметрами
R, L, С
схемы (рис. 3.32
а)
таким образом, что
(3.87)
где к —
некоторое произвольное число (масштабный множитель преоб-разования), Ом2, то
(3.88)
С учетом равенства (3.88) перепишем уравнение (3.86) следующим об-разом:
(3.89)
Из сопоставления уравнений (3.85) и (3.89) следует, что если ток Jэ
источника тока в схеме на рис. 3.32
б
изменяется с той же угловой частотой, что и ЭДС
Е
в схеме на рис. 3.32
а
, и численно равен
E
, а параметры обеих схем согласованы в соответствии с уравнением (3.87), то при
к =
1Ом 2. закон изменения во времени потенциала
φ0
в схеме на рис. 3.32
б
совпадет с законом изменения во времени тока
I
в схеме на рис. 3.32
а.
Если свойства какой-либо из схем изучены, то они полностью могут быть перенесены на дуальную ей схему.
Между входным сопротивлением Zисх
исходного двухполюсника и входной проводимостью
Yдуал
дуального ему двухполюсника существует соотношение
Zисх =k Yдуал
Из (3.88) получаем соотношение между частотной характеристикой чисто реактивного исходного двухполюсника Хисх(ω)
и частотной характеристикой дуального ему тоже чисто реактивного двухполюсника
b дуал (ω).
Каждому элементу исходной схемы (схемы с источниками ЭДС
E
и параметрами
R, L,
С) отвечает свой элемент эквивалентной дуальной схемы (схемы с источниками тока
J3
и параметрами
gэ, Сэ, Lэ
).
Синусоидальный ток и основные характеризующие его величины.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (рис. 3.1):
(3.1)
Максимальное значение функции называют амплитудой.
Амплитуду тока обозначают
Im.
Период Т
— это время, за которое совершается одно полное колебание.
Рисунок 3.1
Частота f —
число колебаний в 1 с (единица частоты
f —
герц (Гц) или с-1):
(3.2)
Угловая частота (единица угловой частоты — рад/с или с-1)
(3.3)
Аргумент синуса, т. е. ( t
+ ), называют
фазой —
характеризует состояние колебания (числовое значение) в данный момент времени
t
.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью различных полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ).
Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их
е
и
j
(или
e(t)
и
j
(
t
)).
1Следующая ⇒
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? — задался я вопросом…
Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем…
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: