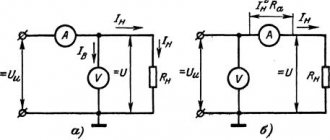
Alternating current is an electric current whose direction and strength changes periodically. Since the strength of alternating current usually changes according to a sinusoidal law, alternating current represents sinusoidal fluctuations in voltage and current.
Therefore, everything that applies to sinusoidal electrical oscillations applies to alternating current. Sinusoidal oscillations are oscillations in which the oscillating quantity changes according to the sine law. In this article we will talk about the parameters of alternating current.
The change in EMF and the change in current of the linear load connected to such a source will occur according to a sinusoidal law. In this case, alternating EMF, alternating voltages and currents, can be characterized by their main four parameters:
There are also auxiliary parameters:
Next, we will consider all these parameters separately and in interrelation.
A period is the time during which a system oscillating passes through all intermediate states and then returns to its original state.
The period T of alternating current is the period of time during which the current or voltage makes one complete cycle of changes.
Since the source of alternating current is a generator, the period is related to the speed of rotation of its rotor, and the higher the speed of rotation of the coil or rotor of the generator, the smaller the period of the generated variable EMF, and, accordingly, the alternating current of the load.
The period is measured in seconds, milliseconds, microseconds, nanoseconds, depending on the specific situation in which the current is considered. The above figure shows how the voltage U changes over time, while having a constant characteristic period T.
Frequency f is the reciprocal of the period, and is numerically equal to the number of periods of change in current or EMF in 1 second. That is, f = 1/T. The unit of frequency is the hertz (Hz), named after the German physicist Heinrich Hertz, who made significant contributions to the development of electrodynamics in the 19th century. The shorter the period, the higher the frequency of change of the emf or current.
Today in Russia the standard frequency of alternating current in electrical networks is 50 Hz, that is, 50 oscillations of the mains voltage occur in 1 second.
In other areas of electrodynamics, higher frequencies are used, for example, 20 kHz or more in modern inverters, and up to several MHz in narrower areas of electrodynamics. The figure above shows that in one second there are 50 complete oscillations, each lasting 0.02 seconds, and 1/0.02 = 50.
From the graphs of changes in sinusoidal alternating current over time, it can be seen that currents of different frequencies contain different numbers of periods in the same period of time.
Angular frequency is the number of oscillations performed in 2pi seconds.
In one period, the phase of the sinusoidal EMF or sinusoidal current changes by 2pi radians or 360°, so the angular frequency of the alternating sinusoidal current is equal to:
Use the number of oscillations per 2pi sec. (and not in 1 second) is convenient because in formulas expressing the law of change in voltages and currents during harmonic oscillations, expressing inductive or capacitive resistance to alternating current, and in many other cases, the oscillation frequency n appears together with the factor 2pi.
Phase is a state, stage of a periodic process. The concept of phase has a more specific meaning in the case of sinusoidal oscillations. In practice, it is usually not the phase itself that plays a role, but the phase shift between any two periodic processes.
In this case, the term “phase” is understood as the stage of development of the process, and in this case, in relation to alternating currents and sinusoidal voltages, the phase is the state of the alternating current at a certain point in time.
In the figures you can see: the coincidence of voltage U1 and current I1 in phase, voltages U1 and U2 in antiphase, as well as a phase shift between current I1 and voltage U2. The phase shift is measured in radians, fractions of a period, or degrees.
Amplitude Um and Im
When talking about the magnitude of a sinusoidal alternating current or a sinusoidal alternating emf, the largest value of the emf or current is called the amplitude or amplitude (maximum) value.
Amplitude
- the greatest value of a quantity that performs harmonic oscillations (for example, the maximum value of current in an alternating current, the deviation of an oscillating pendulum from the equilibrium position), the greatest deviation of an oscillating quantity from a certain value, conventionally accepted as the initial zero.
Alternating electric current
Alternating electric current
(AC, abbreviation for alternating current) is an electric current that changes in magnitude and direction with a certain periodicity. In electrical engineering, it is customary to use the tilde sign (
Sources of alternating electric current are alternating current generators, which create alternating electromotive force, the change in magnitude and direction of which occurs at certain intervals.
AC period and frequency
The time during which one complete change in the emf occurs, that is, one cycle of oscillation or one full revolution of the radius vector, is called the period of alternating current oscillation (Figure 1).
Figure 1. Period and amplitude of a sinusoidal oscillation. Period is the time of one oscillation; Amplitude is its greatest instantaneous value.
The period is expressed in seconds and denoted by the letter T.
Smaller units of measurement of period are also used: millisecond (ms) - one thousandth of a second and microsecond (μs) - one millionth of a second.
1 ms = 0.001 sec = 10 -3 sec.
1 μs = 0.001 ms = 0.000001 sec = 10 -6 sec.
The number of complete changes in the emf or the number of revolutions of the radius vector, that is, in other words, the number of complete cycles of oscillations performed by alternating current within one second, is called alternating current oscillation frequency .
Frequency is designated by the letter f and is expressed in cycles per second or hertz.
One thousand hertz is called a kilohertz (kHz), and a million hertz is called a megahertz (MHz). There is also a unit of gigahertz (GHz) equal to one thousand megahertz.
1000 Hz = 10 3 Hz = 1 kHz;
1000 000 Hz = 10 6 Hz = 1000 kHz = 1 MHz;
1000 000 000 Hz = 10 9 Hz = 1000 000 kHz = 1000 MHz = 1 GHz;
The faster the EMF changes, that is, the faster the radius vector rotates, the shorter the oscillation period. The faster the radius vector rotates, the higher the frequency. Thus, the frequency and period of alternating current are quantities inversely proportional to each other. The larger one of them, the smaller the other.
The mathematical relationship between the period and frequency of alternating current and voltage is expressed by the formulas
For example, if the current frequency is 50 Hz, then the period will be equal to:
T = 1/f = 1/50 = 0.02 sec.
And vice versa, if it is known that the period of the current is 0.02 sec, (T = 0.02 sec.), then the frequency will be equal to:
f = 1/T=1/0.02 = 100/2 = 50 Hz
The frequency of alternating current used for lighting and industrial purposes is exactly 50 Hz.
Frequencies between 20 and 20,000 Hz are called audio frequencies. Currents in radio station antennas oscillate with frequencies up to 1,500,000,000 Hz or, in other words, up to 1,500 MHz or 1.5 GHz. These high frequencies are called radio frequencies or high frequency vibrations.
Finally, currents in the antennas of radar stations, satellite communication stations, and other special systems (for example, GLANASS, GPS) fluctuate with frequencies of up to 40,000 MHz (40 GHz) and higher.
Basic parameters of alternating current
When connected to an alternating current source with a sinusoidally varying e.g.
d.s. electrical circuits with linear resistances will have sinusoidally varying voltages acting in them and sinusoidally varying currents will pass through them. Alternating currents, e. d.s. and voltages are characterized by four main parameters: period, frequency, amplitude and effective value. Period. The period of time during which e. d.s, voltage and or current undergo a complete cycle of changes, called a period. The faster the coil or rotor of an alternating current generator rotates, the shorter the period of change in e. d.s. or current.
Frequency. Number of complete periods of change e. d.s, voltage or current in 1 s is called frequency,
f = 1/T
It is measured in hertz (Hz), i.e. the number of periods per second. The higher the frequency, the shorter the period of change in current, voltage or e. d.s. . In the Soviet Union, all alternating current power plants produce a current varying with a frequency of 50 Hz, i.e. 50 cycles per second. In automation and radio engineering, electric currents of higher frequencies are used. Such frequencies are measured in kilohertz (1 kHz = 10 3 Hz) and megahertz (1 MHz = 10 6 Hz).
Amplitude. The largest value of alternating current (alternating emf and voltage) is called the amplitude value, or amplitude.
Effective value . Current, voltage, etc. d. s, acting in an electrical circuit at each individual moment in time, are determined by the so-called instantaneous values. However, judge the variables e. d.s, current or voltage by their instantaneous values is inconvenient, since these values are continuously changing. Therefore, it is customary to evaluate the ability of alternating current to perform mechanical work or create heat by its effective value. The effective value of alternating current is understood as the strength of such a direct current, which, passing through a conductor for some time, will release in it the same amount of heat as a given alternating current
RMS values of current, voltage and e. d.s. denoted by I, U, E, respectively.
19. The effective (effective) value of the alternating current is the magnitude of the direct current, the action of which will produce the same work (thermal or electrodynamic effect) as the alternating current in question during one period. In modern literature, the mathematical definition of this quantity is more often used - the root mean square value of the alternating current.
In other words, the effective current value can be determined by the formula:
.
For harmonic current oscillations
The effective values of EMF and voltage are determined in a similar way.
21. ACTIVE RESISTANCE IN AC CIRCUIT
The resistance included in the alternating current circuit in which electrical energy is converted into useful work or thermal energy is called active resistance
.
Active resistances at industrial frequency (50 Hz) include, for example, incandescent electric lamps and electric heating devices.
Let's consider an alternating current circuit (Fig. 53), which includes active resistance. In such a circuit, alternating current flows under the influence of alternating voltage. The change in current in a Circuit, according to Ohm's law, depends only on the change in voltage connected to its terminals. When the voltage is zero, the current in the circuit is also zero. As the voltage increases, the current in the Circuit increases and at the maximum voltage value the current becomes greatest. As the voltage decreases, the current decreases. When the voltage changes its direction, the current also changes its direction, etc.
From the above it follows that in an alternating current circuit with active resistance, as the magnitude and direction of the voltage changes, the magnitude and direction of the current simultaneously change proportionally. This means that the current and voltage are in phase.
Let's construct a vector diagram of the effective values of current and voltage for a circuit with active resistance. To do this, capture the voltage vector on a selected horizontal scale. To show on a vector diagram that the voltage and current in the circuit are in phase (j=0), plot the current vector I in the direction of the voltage vector.
The current strength in such a circuit is determined by Ohm's law:
In this circuit, the average value of power consumed by the active resistance is expressed as the product of the effective values of current and voltage.
24.
| Capacitance in an AC circuit |
| When a capacitor is connected to a direct voltage circuit, the current strength is I = 0, and when a capacitor is connected to an alternating voltage circuit, the current strength is I? 0. Consequently, a capacitor in an alternating voltage circuit creates less resistance than in a direct current circuit. |
| The instantaneous voltage value is . The instantaneous value of the current is: Thus, voltage fluctuations lag behind current fluctuations in phase by π/2. |
| Because According to Ohm's law, the current strength is directly proportional to the voltage, then for the maximum values of current and voltage we obtain: , where is the capacitance. |
| Capacitance is not a characteristic of a conductor, because depends on the circuit parameters (frequency). |
| The higher the frequency of the alternating current, the better the capacitor passes current (the lower the capacitor's resistance to alternating current). |
| Because the phase difference between current and voltage fluctuations is π/2, then the power in the circuit is 0: energy is not consumed, but energy is exchanged between the voltage source and the capacitive load. This load is called reactive. |
| 22. Inductive reactance in an alternating current circuit |
| In a coil connected to an alternating voltage circuit, the current strength is less than the current strength in a constant voltage circuit for the same coil. Consequently, the coil in an alternating voltage circuit creates more resistance than in a direct voltage circuit. |
| Instantaneous current value: |
| The instantaneous value of the voltage can be established, taking into account that u = - εi, where u is the instantaneous value of the voltage, and εi is the instantaneous value of the self-induction emf, i.e., when the current changes in the circuit, a self-induction emf appears, which, in accordance with the law of electromagnetic induction and Lenz's rule is equal in magnitude and opposite in phase to the applied voltage. |
| . Therefore, where is the voltage amplitude. The voltage leads the current in phase by π/2. |
| Because According to Ohm's law, the current strength is directly proportional to voltage and inversely proportional to resistance, then taking the value ωL as the coil resistance to alternating current, we obtain: - Ohm's law for a circuit with a purely inductive load. |
| The value is inductive reactance. |
| That. at any instant of time, a change in current strength is counteracted by self-induction emf. Self-induced emf is the cause of inductive reactance. |
| Unlike active resistance, inductive resistance is not a characteristic of a conductor, because depends on the parameters of the circuit (frequency): the higher the frequency of the alternating current, the greater the resistance that the coil provides to it. |
| Because the phase difference between current and voltage fluctuations is π/2, then the power in the circuit is 0: energy is not consumed, but energy is exchanged between the voltage source and the inductive load. This load is called reactive. |
25. Voltage resonance is a resonance that occurs in a series oscillating circuit when it is connected to a voltage source whose frequency coincides with the natural frequency of the circuit.
Let there be an oscillatory circuit with a natural frequency f
, and let an alternating current generator of the same frequency
f
.
At the initial moment, the circuit capacitor is discharged, the generator does not work. After switching on, the voltage across the generator begins to increase, charging the capacitor. At first the coil does not pass current due to self-induction emf. The voltage on the generator reaches its maximum, charging the capacitor to the same voltage.
Next: the capacitor begins to discharge to the coil. The voltage across it drops at the same rate as the voltage across the generator decreases.
Next: the capacitor is discharged to zero, all the energy of the electric field present in the capacitor is converted into the energy of the magnetic field of the coil. At this moment the voltage at the generator terminals is zero.
Further: since the magnetic field cannot exist stationary, it begins to decrease, crossing the turns of the coil in the opposite direction. An induced emf appears at the coil terminals, which begins to recharge the capacitor. A current flows in the circuit of the oscillatory circuit, only in the opposite direction to the charge current, since the turns are crossed by the field in the opposite direction. The capacitor plates are recharged with charges opposite to the original ones. At the same time, the voltage on the generator of the opposite sign increases, and at the same speed with which the coil charges the capacitor.)
Next: the coil recharged the capacitor to maximum voltage. By this time, the voltage on the generator had also reached its maximum.
The following situation arose. The capacitor and the generator are connected in series and the voltage on both is equal to the voltage of the generator. When power supplies are connected in series, their voltages are added.
Consequently, in the next half-cycle, double the voltage will go to the coil (both from the generator and the capacitor), and oscillations in the circuit will occur at double the voltage on the coil.
In low-Q circuits, the voltage on the coil will be less than doubled, since part of the energy will be dissipated (by radiation, by heating) and the energy of the capacitor will not be completely converted into the energy of the coil). The generator and part of the capacitor are connected in series.
27. Power factor is a dimensionless physical quantity that characterizes the consumer of alternating electric current from the point of view of the presence of a reactive component in the load. Power factor shows how much the alternating current flowing through a load is out of phase relative to the voltage applied to it.
Numerically, the power factor is equal to the cosine of this phase shift.
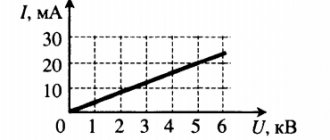
It can be shown that if a sinusoidal current source (for example, a socket
220 V, 50 Hz) load on a load in which the current is ahead or behind in phase by a certain angle from the voltage, then increased power is released at the internal active resistance of the source. In practice, this means that when operating a load with shifted voltage and current, more energy is required from the power plant; the excess energy transferred is released as heat in the wires and can be quite significant.
Equal to the ratio of the active power consumed by the electrical receiver to the total power. Active power is spent to perform work. Apparent power is the geometric sum of active and reactive powers (in the case of sinusoidal current and voltage). In general, the total power can be defined as the product of the effective (rms) values of current and voltage in the circuit. The total power is equal to the square root of the sum of the squares of the active and inactive powers. It is customary to use the volt-ampere (VA) instead of the watt (W) as a unit of measurement for apparent power.
According to the Cauchy-Bunyakovsky inequality, active power, equal to the average value of the product of current and voltage, always does not exceed the product of the corresponding root-mean-square values. Therefore, the power factor takes values from zero to one (that is, from 0 to 100%).
Power factor can be mathematically interpreted as the cosine of the angle between the current and voltage vectors. Therefore, in the case of sinusoidal voltage and current, the value of the power factor coincides with the cosine of the angle by which the corresponding phases lag.
In the electric power industry, the designation for power factor is cos φ (where φ is the phase shift between current and voltage) or λ. When λ is used to indicate power factor, its value is usually expressed as a percentage.
If there is a reactive component in the load, in addition to the power factor value, sometimes the nature of the load is also indicated: active-capacitive or active-inductive. In this case, the power factor is called leading or lagging, respectively.
In the case of sinusoidal voltage, if the load does not have a reactive component, the power factor is equal to the fraction of the power of the first harmonic current in the total power consumed by the load, and is equal to the current distortion factor.
Source
Angular (cyclic) frequency of alternating current.
The rotation speed of the radius vector, i.e., the change in the rotation angle within one second, is called the angular (cyclic) frequency of alternating current and is denoted by the Greek letter ? (omega). The angle of rotation of the radius vector at any given moment relative to its initial position is usually measured not in degrees, but in special units - radians.
A radian is the angular value of an arc of a circle, the length of which is equal to the radius of this circle (Figure 2). The entire circle that makes up 360° is equal to 6.28 radians, that is, 2
.
Figure 2. Radian.
1rad = 360°/2
Consequently, the end of the radius vector during one period covers a path equal to 6.28 radians (2
). Since within one second the radius vector makes a number of revolutions equal to the frequency of the alternating current f, then in one second its end covers a path equal to 6.28 * f radians. This expression characterizing the rotation speed of the radius vector will be the angular frequency of the alternating current - ? .
? = 6.28*f = 2f
ALTERNATING CURRENT. MAIN PARAMETERS
Alternating current is an electric current that periodically changes in magnitude and direction.
To produce alternating current, electric machine generators are used, the operation of which is based on the phenomenon of electromagnetic induction. Alternating current is of great practical importance. Almost all electricity is generated in the form of alternating current power.
The ability to receive alternating current of various voltages (high - for transmitting energy over long distances, low - for powering various consumers), simplicity of design of alternating current generators and motors, reliability of their operation, ease of operation and high technical characteristics
gave them widespread use.
The most widely used is sinusoidal current. The change in current according to a sinusoidal law occurs smoothly, without jumps or sudden changes, which has a beneficial effect on the operation of electrical machines and devices.
The timing diagram of the sinusoidal current is shown in Fig. 1. Its instantaneous value is described by the formula
Where
— maximum value (amplitude) of the current; — angular frequency; — initial phase (the value of the argument at the initial moment of time, i.e. at t = 0).
Alternating EMF, alternating voltage and alternating current are characterized by period, frequency, instantaneous, maximum values, effective value.
Rice. .1. Timing diagram of sinusoidal current
Period. The time during which an alternating emf (voltage or current) makes one complete change in magnitude and direction (one cycle) is called a period. The period is designated by the letter T and is measured in seconds (s).
Frequency . The number of complete changes in the variable EMF (voltage or current) completed in 1 s is called frequency. The frequency is indicated by the letter
and is measured in Hertz (Hz). When measuring high frequencies, kilohertz (kHz) and megahertz (MHz) units are used:
1 kHz = 1,000 Hz, 1 MHz = 1,000 kHz = 1,000,000 Hz.
The higher the frequency of the alternating current, the shorter the period. Thus, frequency is the reciprocal of period:
When a coil rotates in a magnetic field, one revolution corresponds to 360°, or 2 radians. The angular speed of rotation of this turn is expressed in radians per second (rad/s) and is determined by the ratio
. This quantity is called the angular frequency and is denoted by the letter:
Angular frequency of current
expressed in radians per second, times the frequency of the current expressed in hertz
Instantaneous and maximum values . The magnitudes of the variable EMF, current, voltage and power at any time are called the instantaneous values of these quantities and are designated, respectively, by lowercase letters (,
, , ) and written as follows:
The maximum value (amplitude) of the EMF variable (voltage or current) is the greatest value that it reaches in one period. The maximum value of electromotive force is indicated
, voltage -
Um, current -
Effective value . The effective value of alternating current is the strength of direct current that, flowing through equal resistance and in the same time as alternating current, releases the same amount of heat
Source
AC phase.
The angle of rotation of the radius vector at any given instant relative to its initial position is called the phase of the alternating current . The phase characterizes the magnitude of the EMF (or current) at a given instant or, as they say, the instantaneous value of the EMF, its direction in the circuit and the direction of its change; phase indicates whether the emf is decreasing or increasing.
Figure 3. AC phase.
A full rotation of the radius vector is 360°. With the beginning of a new revolution of the radius vector, the EMF changes in the same order as during the first revolution. Consequently, all phases of the EMF will be repeated in the same order. For example, the phase of the EMF when the radius vector is rotated by an angle of 370° will be the same as when rotated by 10°. In both of these cases, the radius vector occupies the same position, and, therefore, the instantaneous values of the emf will be the same in phase in both of these cases.
DID YOU LIKE THE ARTICLE? SHARE WITH YOUR FRIENDS ON SOCIAL NETWORKS!
Source
Sinusoidal current and the main quantities characterizing it.
Page 1 of 6Next ⇒Sinusoidal current and the main quantities characterizing it.
Sinusoidal current is a current that changes over time according to a sinusoidal law (Fig. 3.1):
(3.1)
The maximum value of the function is called the amplitude.
The current amplitude is denoted by
Im.
Period T
is the time it takes to complete one complete oscillation.
Figure 3.1
Frequency f -
number of oscillations in 1 s (frequency unit
f -
hertz (Hz) or s-1):
(3.2)
Angular frequency (unit of angular frequency - rad/s or s-1)
(3.3)
The sine argument, i.e. ( t
+ ), called
phase -
characterizes the state of oscillation (numerical value) at a given time
t
.
Any sinusoidally varying function is determined by three quantities: amplitude, angular frequency and initial phase.
Sinusoidal currents and EMF of relatively low frequencies (up to several kilohertz) are obtained using synchronous generators (they are studied in the course of electrical machines). Sinusoidal currents and high-frequency EMF are obtained using various semiconductor generators (discussed in detail in the radio engineering course and in less detail in the TOE course).
A source of sinusoidal EMF and a source of sinusoidal current are designated on electrical diagrams in the same way as sources of constant EMF and current, but they are designated
e
and
j
(or
e(t)
and
j
(
t
)).
Average and effective values of a sinusoidally varying quantity.
Below the average
a sinusoidally varying quantity is understood as its average value over half a period. Average current
(3.4)
i.e., the average value of the sinusoidal current is 2/ = 0.638 of the amplitude. Likewise,
Eav = 2Em/ ; Uav = 2Um/ .
of effective value is widely used
a sinusoidally varying value (it is also called effective or root mean square). RMS current value
(3.5)
Consequently, the effective value of the sinusoidal current is equal to 0.707 of the amplitude current. Likewise
Effective value of sinusoidal current I
is numerically equal to the value of such a direct current, which, in a time equal to the period of the sinusoidal current, releases the same amount of heat as the sinusoidal current.
Most measuring instruments show the effective value of the measured quantity.
Amplitude coefficient ka -
this is the ratio of the amplitude of a periodically changing function to its effective value. For sinusoidal current
(3.6)
The form factor kf is understood as the ratio of the effective value of a periodically changing function to its average value over half a period. For sinusoidal current
(3.7)
Addition and subtraction of sinusoidal functions of time on the complex plane. Vector diagram.
Let us assume that it is necessary to add two currents ( i1
and
i2
) of the same frequency. Their sum gives a certain current of the same frequency:
It is required to find the amplitude It
and the initial phase
ψ
of current
i
.
For this purpose, we represent the current i1
on the complex plane (Fig. 3.4) by the vector =
I1тejψ1
, and the current
i2
- by the vector =
I2тejψ2.
The geometric sum of vectors and
I2т
will give the complex amplitude of the total current
Iт = Iт
e-jψ2.
The current amplitude It
is determined by the length of the total vector, and the initial phase
ψ
is determined by the angle formed by this vector and the + 1 axis.
Figure 3.4
To determine the difference between two currents (EMF, voltages), it is necessary to perform not addition, but subtraction of the corresponding vectors on the complex plane.
Let us pay attention to the fact that if the vectors , ,It
began to rotate around the origin with angular velocity ω, then the relative position of the vectors relative to each other would remain unchanged.
A vector diagram is a set of vectors on the complex plane depicting sinusoidally varying functions of time of the same frequency and constructed in compliance with their correct orientation relative to each other in phase. Example in Fig. 3.4.
Instant power.
The flow of sinusoidal currents through sections of the electrical circuit is accompanied by the consumption of energy from sources. The rate of energy supply is characterized by power. Under the instantaneous power value, or under the instantaneous power,
understand the product of the instantaneous value of voltage
and
in a section of the circuit by the instantaneous value of current
i
flowing through this section:
(3.14)
where p -
function of time.
Before we begin to study the basics of calculating complex sinusoidal current circuits, we will consider the relationships between currents and voltages in the simplest circuits, vector diagrams for them and curves of instantaneous values of various quantities. The elements of real sinusoidal current circuits are resistors, inductive coils and capacitors. The flow of sinusoidal current is resisted by resistive elements (resistors) - they release energy in the form of heat - and reactive elements (inductive coils and capacitors) - they either store energy in the magnetic (electric) field or release it. Let's look at the behavior of these elements.
Complex conductivity.
Under complex conductivity Y
understand the reciprocal of the complex resistance Z:
(3.37)
The unit of complex conductivity is cm (Ohm-1). Its real part is denoted by g,
imaginary - through
b.
Because
That
(3.38)
If X
is positive, then
b
is positive.
When X
is negative,
b
is also negative.
When using complex conductivity, Ohm's law (3.35) is written as follows:
(3.39)
or
where Ia
— active component of the current;
Ir is
the reactive component;
current; U is
the voltage at the section of the circuit whose resistance is equal to Z.
Definition of a dual chain.
Two electrical circuits are called dual,
if the law of change in loop currents in one of them is similar to the law of change in nodal potentials in the other.
The original and its dual schemes are called mutually inverse.
As a simple example in Fig. Figure 3.32 shows two dual chains.
Fig.3.32.
Scheme in Fig. 3.32, a
consists of an EMF source
E
and active, inductive and capacitive elements (R, L, C) connected in series with it
.
Scheme in Fig.
3.32 b
consists of a current source
J3
and three parallel branches.
The first branch contains active conductivity gе,
the second - capacitance
Se,
the third - inductance
Ze
.
In order to show what kind of correspondence takes place in dual circuits, let us draw up for the circuit in Fig. 3.32, a
equation using the loop current method:
(3.85)
and for the diagram in Fig. 3.32 b —
using the method of nodal potentials, denoting the potential of point
a
by φa, setting the potential of the second node equal to zero:
(3.86)
If the parameters ge, Le. Se
, the circuit (Fig. 3.32
b)
is coordinated with the parameters
R, L, C of
the circuit (Fig. 3.32
a)
in such a way that
(3.87)
where k -
some arbitrary number (scale transformation factor), Ohm2, then
(3.88)
Taking into account equality (3.88), we rewrite equation (3.86) as follows:
(3.89)
From a comparison of equations (3.85) and (3.89) it follows that if the current Jе
current source in the circuit in Fig.
3.32 b
changes with the same angular frequency as the emf
E
in the circuit in Fig.
3.32 a
, and is numerically equal to
E
, and the parameters of both circuits are consistent in accordance with equation (3.87), then at
k =
1 Ohm 2. the law of the change in time of the potential
φ0
in the circuit in Fig.
3.32 b
will coincide with the law of change in time of current
I
in the circuit in Fig.
3.32 a.
If the properties of any of the schemes are studied, then they can be completely transferred to the scheme dual to it.
Between the input impedance Zout
of the original two-terminal network and the input conductivity
Ydual
of the dual-terminal network, there is a relation
Zout =k Ydual
From (3.88) we obtain the relationship between the frequency response of the purely reactive original two-terminal network Xx(ω)
and the frequency response of its dual, also purely reactive two-terminal network
b dual (ω).
Each element of the original circuit (circuits with emf sources
E
and parameters
R, L,
C) corresponds to its own element of the equivalent dual circuit (circuits with current sources
J3
and parameters
gе, Se, Le
).
Sinusoidal current and the main quantities characterizing it.
Sinusoidal current is a current that changes over time according to a sinusoidal law (Fig. 3.1):
(3.1)
The maximum value of the function is called the amplitude.
The current amplitude is denoted by
Im.
Period T
is the time it takes to complete one complete oscillation.
Figure 3.1
Frequency f -
number of oscillations in 1 s (frequency unit
f -
hertz (Hz) or s-1):
(3.2)
Angular frequency (unit of angular frequency - rad/s or s-1)
(3.3)
The sine argument, i.e. ( t
+ ), called
phase -
characterizes the state of oscillation (numerical value) at a given time
t
.
Any sinusoidally varying function is determined by three quantities: amplitude, angular frequency and initial phase.
Sinusoidal currents and EMF of relatively low frequencies (up to several kilohertz) are obtained using synchronous generators (they are studied in the course of electrical machines). Sinusoidal currents and high-frequency EMF are obtained using various semiconductor generators (discussed in detail in the radio engineering course and in less detail in the TOE course).
A source of sinusoidal EMF and a source of sinusoidal current are designated on electrical diagrams in the same way as sources of constant EMF and current, but they are designated
e
and
j
(or
e(t)
and
j
(
t
)).
1Next ⇒
What will happen to the Earth if its axis shifts by 6666 km? What will happen to the Earth? - I asked myself...
What makes your dreams come true? One hundred percent, unshakable confidence in your...
Conflicts in family life. How can I change this? It is rare that a marriage and relationship exists without conflict and tension. Everyone goes through this...
System of Protected Areas in the USA The study of specially protected natural areas (SPNA) in the USA is of particular interest for many reasons...
Didn't find what you were looking for? Use Google search on the site: