Теория и модель
Реальный трансформатор работает по принципу наведение ЭДС индукции входным переменным током. Линии магнитной индукции распространяются по ферромагнитными сердечниками и пронизывают витки вторичных обмоток. Магнитный поток порождает переменный электрический ток с такой же частотой, как на входе первичной катушки.
ЭДС индукции возникает на витках всех обмоток, а также в магнитопроводе. Вихревые токи в сердечнике создают дополнительное сопротивление. Часть мощностей переменных напряжений, поступающих в цепи первичных обмоток, расходуется на преодоление сопротивлений и выделяется в виде тепла. Поэтому КПД реального трансформатора хотя и довольно высокий, но никогда не достигает 100%.
Теоретически можно представить себе мнимый аппарат со 100-процентным КПД.
Для этого предположим, что:
- обе обмотки индуктивные;
- активное сопротивление обмоток равняется нулю;
- отсутствует гистерезис, вызванный перемагничиванием магнитопровода;
- отсутствуют токи Фуко в сердечнике;
- магнитные потоки не рассеиваются, а циркулируют по идеальному магнитопроводу.
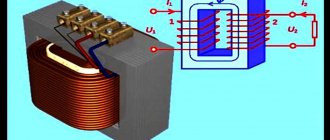
У аппарата с такими свойствами вся энергия, поступающая на вход первичной обмотки, преобразуется в напряжение во вторичной обмотке без каких-либо потерь. То есть, мы получим идеальный трансформатор (рис. 1).
Рис. 1. Модель идеального трансформатора
На рисунке показан двухобмоточный прибор.Но нам ничего не стоит идеализировать семейство силовых трансформаторов с несколькими обмотками. Модель идеального трансформатора мы можем применить для трехфазных трансформаторов (рис. 2),и для других типов устройств, например для тороидальных трансформаторов (рис. 3).
Рис. 2. Трехфазный трансформатор
Рис. 3. Тороидальная модель трансформатора
Рабочий процесс трансформатора
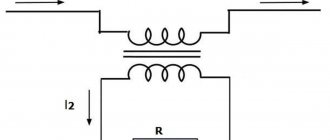
Процесс работы трансформатора рассмотрим на основе эквивалентной схемы замещения из предыдущей статьи
Эквивалентная схема замещения трансформатора.
При наличии нагрузки ZH на выводах вторичной обмотки 3-4 и напряжении U1 на выводах первичной обмотки 1-2 в магнитопроводе трансформатора создается магнитный поток, который индуцирует в обмотках ЭДС: в первичной – Е1, а во вторичной – Е2. В результате приложенное напряжение в первичной обмотке U1 уравновешивается ЭДС Е1 и падением напряжения на активном сопротивлении обмотки R1 и реактивном сопротивлении Ls1 индуктивности рассеяния. Аналогичным образом происходит уравновешивание напряжения и во вторичной обмотке трансформатора.
Определение основных параметров трансформатора: напряжения U1 и U1, ЭДС Е1 и Е2, потери в обмотках и в магнитопроводе происходит при рассмотрении режимов работы трансформатора, а определение их реальных значений – из опытов холостого хода и короткого замыкания.
Уравнение идеального трансформатора
Мнимому идеальному устройству приписывается свойство: отношение первичного и вторичного напряжений обратно пропорционально отношению комплексного электрического тока в первичной и вторичной катушках. Для идеального прибора справедливо уравнение, которое называют уравнением идеального трансформатора.
U1 / U2 = I2 / I1 = N1 / N2 = n, гдe N — количество витков.
Число n является коэффициентом трансформации придуманного идеального трансформатора.
Из уравнения видно, что при увеличении напряжения в цепи вторичной обмотки, электрический ток во столько же раз уменьшается в этой цепи. То есть, существует обратно пропорциональная зависимость между выходным током и напряжением. Эта зависимость существует и в реальных приборах, но в таких аппаратах линейность немного нарушается из-за тепловых потерь.
Если к вторичной обмотке подключить внешнюю нагрузку с комплексным сопротивлением Z2 , то входное сопротивление Zвх будет в n2 раз больше сопротивления этой нагрузки Zвх = U1 / I1 = n* U1 / ( I1 / n) = n2*Z2
Если такую нагрузку имеющую комплексное сопротивление Z1 подсоединить к первичной катушке, а питание подать на вторичную, то получим: Z2вх = Z1 / n2.
Данные соотношения характеризуют для идеального аппарата превращение сопротивлений. В частности, при разомкнутой вторичной обмотке Z1вх = ∞, а при замкнутых Z1вх = 0.
Свойства реального аппарата приближаются к свойствам идеального, при условии что коэффициент магнитной связи аппарата стремится к единице, а мощность потерь близится к нулю.
Уравнение токов трансформатора. Формула.
Уравнение токов:
,
где Ix – ток холостого хода трансформатора.
18. Чем отличается приведенный трансформатор от реального? Приведенный трансформатор отличается следующим: 1) число витков вторичной обмотки его равно числу витков первичной обмотки реального трансформатора; 2) активные, реактивные и полная мощности, а также потери вторичных обмоток приведенного и реального трансформаторов соответственно равны. 3) коэффициентом трансформации
k=El/E2=wl/w2=1
Так как число витков приведенной вторичной обмотки равно числу витков первичной, то индуктируемые потоком взаимоиндукции электродвижущие силы обеих обмоток равны, т. е.
Необходимо, чтобы приведенная обмотка была эквивалентна действительной вторичной обмотке. Поэтому потери должны сохраниться:
В приведенной обмотке должны сохраниться те же соотношения между активными и индуктивными падениями напряжений, которые существуют в действительной обмотке. Отсюда получим выражение для индуктивного сопротивления приведенной обмотки
Угол сдвига фаз между ЭДС и магнитным потоком. Число.
сдвиг фаз между E и Ф м = равен 90°
Что определяет намагничивающий ток?
величина намагничивающего тока
и его форма в значительной степени определяются магнитными свойствами магнитопровода трансформатора, которые зависят от величины индукции в стали. При увеличении насыщения магнитопровода намагничивающий ток резко возрастает.
Намагничивающий ток-является главной составляющей тока Х.Х. Этот ток является Реактивным Iр .
Угол сдвига фаз между намагничивающим током и магнитным потоком. Число.
Намагничивающий ток , т.е. реактивная составляющая Iр, совпадает по фазе с магнитным потоком в сердечнике
сдвиг фаз между составляющими . активной Iа и Iр равен 90°.
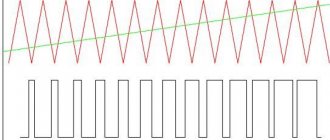
Форма намагничивающего тока трансформатора в режиме насыщения. График.
Рис. 2.3. Построение кривой намагничивающего
тока трансформатора
Если магнитопровод трансформатора не насыщен, то намагничивающий ток −синусоидальный, если магнитопровод насыщен, то ток несинусоидальный. Но в любом случае намагничивающий ток совпадает по фазе с магнитным потоком . Внасыщенном трансформаторе ток определяется по кривой намагничивания представленной на рис.2.3 в первом квадранте.
Чем определяется активная составляющая тока холостого хода?
Активная составляющая тока холостого хода идет на покрытие потерь мощности
(14.4)
Активная составляющая тока холостого хода I
0а =
I
0cosφ0 зависит от потерь холостого хода . Практически
I
0
I
c. Активная составляющая
I
cа, как указывалось, определяется потерями .
Таким образом, активная составляющая тока холостого хода
,
где , и ток холостого хода
.
Чем отличаются постоянные потери в трансформаторе от переменных?
В работающем трансформаторевсегда имеются как магнитные, так и электрические потери. Магнитные потери в трансформаторе слагаются из потерь на вихревые токи и гистерезис:
Величина этих потерь зависит от напряжения U1 и магнитной индукции В. Можно считать, что при U1 = const, рон= В2. Они не зависят от нагрузки, то есть являются постоянными.
Электрические потери в обмотках, наоборот, переменные, то есть:
где ркн — соответствует потерям при коротком замыкании трансформатора.
Что делают, чтобы уменьшить потери на вихревые токи?
Для уменьшения потерь на вихревые токи
- магнитопроводы трансформаторов и других электромагнитных устройств изготавливают не из сплошных масс, а из отдельных пластин, изолированных друг от друга.
- магнитопроводы составляют из листов высоколегированной стали, удельное электрическое сопротивление которой значительно больше, чем обычной стали.
Таким образом, потери на вихревые токи зависят от материала магнитопровода, толщины стальных пластин и изоляции между ними. Кроме того, потери на вихревые токи пропорциональны квадратам частоты и магнитной индукции.
⇐ Предыдущая3Следующая ⇒
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот…
Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право…
Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)…
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Для чего нужна модель идеального прибора?
Идеальный трансформатор часто используется при расчетах реальных конструкций. Он применяется в качестве эквивалента реального устройства в схемах для расчетов и в задачах по построению электрических цепей. (Пример построения схемы см. на рис. 4)
Рис. 4. Пример синтеза схемы
На практике часто приходится делать расчеты однофазных трансформаторов, вычислять параметры тороидальных сердечников, чтобы обеспечить требую мощность тороидальных устройств. От величины однофазной нагрузки зависит то, какую электрическую изоляцию необходимо применить для силовых разделительных моделей.
От режима нагрузки зависит выбор типа охлаждения обмоток конструкций, чтобы обеспечить надежность трансформатора.
Дело в том, что сделать точный расчет реального устройства очень трудно, так как его параметры зависят от переменных магнитных составляющих, в том числе и тех, которые выходят за пределы сердечника. Вихревые токи Фуко создают дополнительные сопротивления нагрузки.
Очень сложно поддается расчету разделительный трансформатор, так как его обмотки налагаются друг на друга, создавая запутанные вихревые токи. Проследить за сдвигом фаз, происходящих в этих переменных токах, почти невозможно.
Задачу упрощает модель идеального прибора. Применяя уравнение для этого мнимого устройства легко вычислить все его параметры. Они не сильно отличаются от параметров соответствующего типа реального аппарата. Относительная погрешность не превышает нескольких процентов, поэтому ею можно пренебречь.
Производя расчеты в различных рабочих режимах реального аппарата, можно с высокой точностью определить величины номинальных нагрузок, пользуясь уравнением для мнимого трансформатора.
Измерительные трансформаторы.
При высоких напряжениях трудно проводить измерения, поскольку высоковольтные приборы дороги и обычно громоздки; их точность подвержена воздействию статического электричества, к тому же они небезопасны. Когда ток превышает 60 А, нелегко обеспечить высокую точность амперметров из-за больших проводов и значительных ошибок, обусловленных паразитным полем концевых выводов. Кроме того, амперметры и катушки тока в высоковольтных цепях опасны для оператора. В измерительных трансформаторах тока и напряжения используются катушки напряжения на 100 В и катушки тока на 5 А. Вторичные обмотки должны быть заземлены. Если шкалы приборов не откалиброваны в коэффициентах трансформации, то показания надо умножать на соответствующий коэффициент трансформации.
Уравнения напряжений и МДС трансформатора
На основании Т-образной схемы замещения можно записать следующие уравнения равновесия напряжений (ЭДС) трансформатора:
U1 = –E1+I1(R1+jX1)= –E1+I1Z1 , (1)
U2’= E2’ – I2’ (R2’+jX2’ )= E2’ – I2’Z2’ . (2)
Особенностью работы трансформатора является то, что ввиду относительной малости сопротивлений R1 и X1 падение напряжения I1Z1 в диапазоне нормальных нагрузок относительно мало, вследствие чего, согласно уравнению (1),
E1 ~ U1. В свою очередь действующее значение ЭДС E1 пропорционально амплитуде магнитного потока в магнитопроводе Фm
U1 ~ E1 = 4,44f1W1Фm, (3) где W1 — число витков фазы первичной обмотки.
Как следует из (3) значение магнитного потока определяется в основном первичным напряжением:
Фm ~ U1/4,44f1W1(4) и при U1 = const также Фm ~ const.
При холостом ходе трансформатор потребляет из сети такой ток Ix = I1, который нужен для создания необходимого потока при данном напряжении U1.
Значение потока Фm всегда таково, что индуктируемая им ЭДС E1 вместе с падением напряжения I1Z1 в соответствии с уравнением (1) уравновешивают приложенное напряжение U1.
При подключении к вторичной обмотке нагрузки в ней протекает ток I2. Магнитодвижущая сила вторичной обмотки (ее число витков W2)
W2I2 = W1I2’ (5).
стремится создать в магнитопроводе свой поток и изменить, таким образом, поток, существовавший в режиме холостого хода. Однако, как отмечено выше, при U1=const этот поток существенным образом измениться не может (см. формулу 4). Поэтому первичная обмотка будет потреблять из сети, кроме намагничивающего тока Ix, дополнительный ток (–I2’) такой величины, что создаваемая им МДС (–W1I2’) уравновесит МДС W1I2’ вторичной обмотки.
Ток (–I2’), уравновешивающий в магнитном отношении вторичный ток I2’, называется нагрузочной составляющей первичного тока.
Полный первичный ток I1 состоит из намагничивающей Ix и нагрузочной (–I2’) составляющих:
I1 = Ix+ (–I2’). (6)
Равенство (6) называется уравнением равновесия МДС обмоток приведенного трансформатора.
Режим нагрузки трансформатора.
Если включить вторичную обмотку трансформатора на внешнюю цепь, замкнув рубильник 4, то трансформатор переходит из режима холостого хода в режим нагрузки.
Очевидно, что с момента включения рубильника в цепи вторичной обмотки появляется ток нагрузки /2. Этот ток, как и любой изменяющийся ток, создает свой переменный магнитный поток Ф2. Большая часть потока Ф2 замыкается по магнигопроводу трансформатора, а меньшая часть Фр2 — по воздуху вокруг витков вторичной обмотки; она составляет магнитный поток рассеяния.
Будучи индуктированным, ток вторичной обмотки по правилу Ленца противодействует причине, его вызвавшей, т. е. имеет направление, противоположное току /о, поэтому и его магнитный поток Ф2 направлен навстречу потоку Фо. Другими словами, лоток, созданный вторичным током, должен был бы ослаблять основной магнитный поток Фо.
Уравнения Кирхгофа для контуров трансформатора.
Приведение чисел витков обмоток и векторная диаграмма трансформатора.
При изучении и анализе режимов работы трансформатора, задача затрудняется тем, что коэффициент трансформации k может иметь относительно большое значение, в связи с чем, возникают трудности с построением векторной диаграммы трансформатора. Проблема решается приведением числа витков вторичной обмотки к числу первичной. Таким образом, коэффициент трансформации станет
Для трансформатора, у которого параметры вторичной обмотки пересчитаны под число витков первичной (приведенного), справедливы следующие уравнения
Определим составляющие этих уравнений, учитывая что, приведение не должно изменить режим работы первичной цепи и энергетические параметры вторичной цепи должны остаться прежними.
При приведении не должна измениться намагничивающая сила вторичной обмотки поэтому
Исходя из того, что электромагнитная мощность вторичной обмотки не должна изменится, найдем приведенную ЭДС вторичной обмотки E’2
Приведенное напряжение вторичной обмотки
Приведенное активное сопротивление, находят при условии равенства потерь во вторичной обмотке
Аналогично находится приведенное индуктивное сопротивление вторичной обмотки при равенстве реактивных мощностей
Приведенное полное сопротивление
Приведенное полное сопротивление нагрузки
Ток I0 – это ток холостого хода, который определяется из опыта холостого хода трансформатора.