Как найти напряжение через индукцию

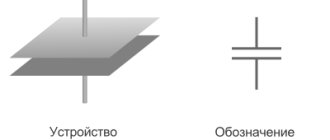
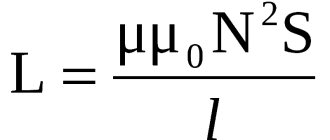Введение

Если бы кому-нибудь пришла в голову идея провести опрос населения Земли на тему «Что вы знаете об индуктивности?», то подавляющее число опрашиваемых просто пожало бы плечами. А ведь это второй по многочисленности вслед за транзисторами технический элемент, на котором зиждется современная цивилизация! Любители детективов, припомнив, что в своей юности зачитывались захватывающими рассказами сэра Артура Конан Дойла о приключениях знаменитого сыщика Шерлока Холмса, с разной степенью уверенности пробормочут что-то о методе, которым вышеозначенный сыщик пользовался. При этом подразумевая метод дедукции, который, наравне с методом индукции, является основным методом познания в западной философии Нового времени.

При методе индукции происходит исследование отдельных фактов, принципов и формирование общих теоретических концепций на основе полученных результатов (от частного к общему). Метод дедукции, наоборот, предполагает исследование от общих принципов, законов, когда положения теории распределяются на отдельные явления.

Следует отметить, что индукция, в смысле метода, не имеет сколько-нибудь прямого отношения к индуктивности, просто они имеют общий латинский корень inductio

— наведение, побуждение — и обозначают совершенно разные понятия.

Лишь малая часть опрашиваемых из числа носителей точных наук — профессиональных физиков, инженеров-электротехников, радиоинженеров и студентов этих направлений — смогут дать внятный ответ на этот вопрос, а некоторые из них готовы прочитать с ходу целую лекцию на эту тему.

Определение индуктивности

В физике индуктивность, или коэффициент самоиндукции, определяется как коэффициент пропорциональности L между магнитным потоком Ф вокруг проводника с током и порождающим его током I или — в более строгой формулировке — это коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током:

или

Для понимания физической роли катушки индуктивности в электрических цепях можно использовать аналогию формулы энергии, запасаемой в ней при протекании тока I, с формулой механической кинетической энергии тела.

При заданной силе тока I индуктивность L определяет энергию магнитного поля W, создаваемого этим током I:

Аналогично, механическая кинетическая энергия тела определяется массой тела m и его скоростью V:

То есть индуктивность, подобно массе, не позволяет энергии магнитного поля мгновенно увеличиться, равно как и масса не позволяет проделать такое с кинетической энергией тела.

Проведём исследование поведения тока в индуктивности:

Рис. 1. Электрическая схема эксперимента

Рис. 2. Физическая реализация эксперимента

Рис. 3. Осциллограмма тока через индуктивность. Желтая осциллограмма — выход сигнал-генератора, голубая — сигнал на резисторе.

Из-за инерционности индуктивности происходит затягивание фронтов входного напряжения. Такая цепь в автоматике и радиотехнике называется интегрирующей, и применяется для выполнения математической операции интегрирования.

Проведём исследование напряжения на катушке индуктивности:

Рис. 4. Электрическая схема эксперимента

Рис. 6. Осциллограмма напряжения на индуктивности (голубая)

В моменты подачи и снятия напряжения из-за присущей катушкам индуктивности ЭДС самоиндукции, возникают выбросы напряжения. Такая цепь в автоматике и радиотехнике называется дифференцирующей, и применяется в автоматике для корректировки процессов в управляемом объекте, носящих быстрый характер.

Рис. 5. По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности.

Как найти напряжение через индукцию

Катушки индуктивности и расчеты
Катушки индуктивности, в отличии от проводников, не обладают стабильным сопротивлением. Однако, для них существует определенная математическая зависимость между напряжением и током :

Как видите, эта формула похожа на аналогичную формулу «Закона Ома» для конденсатора. Она связывает одну переменную (в нашем случае напряжение на катушке индуктивности) со скоростью изменения другой переменной (тока через катушку). И напряжение (u) и скорость изменения тока здесь (di/dt) мгновенны: они берутся в определенный момент времени. Величина скорости изменения тока (di/dt) выражается в амперах в секунду , и имеет положительное значение при увеличении тока, и отрицательное значение при его уменьшении.

Поведение катушки индуктивности (по аналогии с конденсатором) тесно связано с переменной времени. Если не учитывать внутреннее сопротивление катушки индуктивности (ради чистоты эксперимента мы принимаем его равным нулю), то напряжение на ее выводах будет зависеть от изменения тока во времени.

Давайте предположим, что мы подключили идеальную катушку индуктивности (имеющую нулевое сопротивление провода) к цепи, позволяющей измерить ток через эту катушку при помощи потенциометра:

Если механизм потенциометра находится в одном положении (ползунок неподвижен), то соединенный последовательно с ним амперметр зарегистрирует постоянный (неизменный) ток, а подключенный к катушке индуктивности вольтметр покажет 0 вольт. Так как ток в этом случае постоянен, скорость его изменения (di/dt) будет равна нулю. Посмотрев внимательно на вышеприведенное уравнение можно сделать вывод, что при нулевом значении du/dt мгновенное напряжение на катушке так же будет равно нулю. С точки зрения физики, если ток будет постоянным (неизменным), то постоянным будет и произведенное катушкой индуктивности магнитное поле. При отсутствии изменений магнитного потока (dΦ/dt = 0 Вебер в секунду) индуцированное напряжение будет равно нулю.

Если ползунок потенциометра медленно перемещать вверх, то его сопротивление будет медленно уменьшаться. Ток в цепи при этом будет возрастать, что можно увидеть по медленному отклонению стрелки амперметра:

Если ползунок потенциометра перемещать с постоянной скоростью, то ток в цепи будет нарастать равномерно, а значит, отношение di/dt будет иметь фиксированное значение. Это значение, умноженное на индуктивность (так же имеющую фиксированную величину), даст нам постоянное напряжение некоторой величины. С точки зрения физики, постепенное увеличение тока приведет к росту магнитного поля. Увеличивающийся магнитный поток поля создаст в катушке индуцированное напряжение, выраженное уравнением Фарадея: e = N(dΦ/dt). Это напряжение принимает такую полярность, которая пытается противодействовать изменению тока. Другими словами, полярность напряжения, индуцированного в результате увеличения тока, будет ориентирована против направления этого тока, чтобы сохранить его величину на прежнем уровне. Это явление демонстрирует более общий принцип физики, известный как Правило Ленца , который гласит : Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Индуктивность соленоида

Катушка в форме соленоида (конечной длины).

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) B{\displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки является фактически постоянной и (приближённо) равна

B=μNil{\displaystyle \displaystyle B=\mu _{0}Ni/l}

или

B=μni,{\displaystyle \displaystyle B=\mu _{0}ni,}

где μ{\displaystyle \mu _{0}} − магнитная постоянная, N{\displaystyle N} − число витков, i{\displaystyle i} − ток, записанный в амперах , l{\displaystyle l} − длина катушки в метрах и n{\displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{\displaystyle B} , умноженному на площадь поперечного сечения S{\displaystyle S} и число витков N{\displaystyle N}:

Ψ=μN2iSl=μn2iV,{\displaystyle \displaystyle \Psi =\mu _{0}N^{2}iS/l=\mu _{0}n^{2}iV,}

где V=Sl{\displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):

L=μN2Sl=μn2V.{\displaystyle \displaystyle L=\mu _{0}N^{2}S/l=\mu _{0}n^{2}V.}

Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель μ{\displaystyle \mu } — относительную магнитную проницаемость сердечника:

L=μμN2Sl=μμn2V.{\displaystyle \displaystyle L=\mu _{0}\mu N^{2}S/l=\mu _{0}\mu n^{2}V.}

В случае, когда μ>>1{\displaystyle \mu >>1}, можно (следует) под S

понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Расчет катушки индуктивности

Онлайн расчет многослойной катушки. Калькулятор считает по алгоритму с применением эллиптических интегралов Максвелла. Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Индуктивность катушки зависит от ее геометрических размеров, числа витков и способа намотки катушки. Чем больше диаметр, длина намотки и число витков катушки, тем больше ее индуктивность.

Смотрите также

Очень странный результат получается. На 3,4 мГ d20 L35 провод 1/1,2 получается один слой и расход провода менее одного метра. Как это??

Попробуйте поменять микрогенри на милигенри

Может попутали милигенри и микрогенри?

Тут расчет явно без сердечника, иначе были бы другие данные, например проницаемость сердечника.

А как же сердечник? С сердечником или без него?

Ингвар, да чтож вам так нужны букввы НННН? Длина! Дарю.

Длинна намотки это длинна катушки от точки начала намотки до конча рассчитанного проводника(метры), длинна проводника рассчитывается из нужного вам сопротивления. Например для магнитной системы вам надо не менее 1мм и не более 3 (2слоя намотки), а из-за длинны проводника у вас получается 6мм, придется увеличивать число слоев (до 4х) сделать катушку толще, но короче.

Главное индуктивность и сопртивение. Чем длиннее провод, тем больше его сопротивление!

Длина намотки никак не влияет на результаты. Так и должно быть?

Источник

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Советуем изучить Активная антенна для автомобиля

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Индуктивность и конденсатор

Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:

Ce = C : (1 — 4Π2f2LC),

где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.

Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.

Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:

Lk = Lp + Lm + Lb,

где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.

Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:

Lk = Lc : n + µ0 l х d : (3b) + Lb,

где l – длина шин, b – ее ширина, а d – расстояние между шинами.

Измеритель индуктивности для мультиметра

Несмотря на то, что определять индуктивность при работе с электроникой приходится редко, это все же иногда необходимо, а мультиметры с измерением индуктивности найти достаточно трудно. В данной ситуации поможет специальная приставка к мультиметру, позволяющая измерить индуктивность.

Зачастую для подобной приставки используется цифровой мультиметр установленный на измерение напряжения с порогом точности измерения в 200 мВ, который можно приобрести в любом магазине электро и радиоаппаратуры в готовом виде. Это позволит сделать простую приставку к цифровому мультиметру.

Индуктивность соленоида

Катушка в форме соленоида (конечной длины).

Соленоид — катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного сердечника плотность магнитного потока (или магнитная индукция) B{\displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки вдали от её концов (приближённо) равна

B=μNil{\displaystyle \displaystyle B=\mu _{0}Ni/l}

или

B=μni,{\displaystyle \displaystyle B=\mu _{0}ni,}

где μ{\displaystyle \mu _{0}} − магнитная постоянная, N{\displaystyle N} − число витков, i{\displaystyle i} − ток в амперах , l{\displaystyle l} − длина катушки в метрах и n{\displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{\displaystyle B} , умноженному на площадь поперечного сечения S{\displaystyle S} и число витков N{\displaystyle N}:

Ψ=μN2iSl=μn2iV,{\displaystyle \displaystyle \Psi =\mu _{0}N^{2}iS/l=\mu _{0}n^{2}iV,}

где V=Sl{\displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):

L=μN2Sl=μn2V.{\displaystyle \displaystyle L=\mu _{0}N^{2}S/l=\mu _{0}n^{2}V.}

Если катушка внутри полностью заполнена магнитным сердечником, то индуктивность отличается на множитель μ{\displaystyle \mu } — относительную магнитную проницаемость сердечника:

L=μμN2Sl=μμn2V.{\displaystyle \displaystyle L=\mu _{0}\mu N^{2}S/l=\mu _{0}\mu n^{2}V.}

В случае, когда μ>>1{\displaystyle \mu >>1}, под S

можно понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Проведение замеров индуктивности

После сборки приставку к мультиметру необходимо протестировать. Есть несколько способов, как проверить устройство:

1. Определение индуктивности измерительной приставки. Для этого необходимо замкнуть два провода, предназначенных для подключения к индуктивной катушке. Например, при длине каждого провода и перемычки 3 см образуется один виток индукционной катушки. Этот виток обладает индуктивностью 0,1 – 0,2 мкГн. При определении индуктивности свыше 5 мкГн данная погрешность не учитывается в расчетах. В диапазоне 0,5 – 5 мкГн при измерении необходимо брать в расчет индуктивность устройства. Показания менее 0,5 мкГн являются примерными.
2. Измерение неизвестной величины индуктивности. Зная частоту катушки, при помощи упрощенной формулы расчета индуктивности можно определить это значение.
3. В случае, когда порог срабатывания кремниевых p-n переходов выше амплитуды измеряемой электрической цепи (от 70 до 80 мВ), можно измерить индуктивность катушек непосредственно в самой схеме (предварительно обесточив ее). Поскольку собственная емкость приставки имеет большое значение (25330 пФ), погрешность подобных измерений будет составлять не более 5% при условии, что емкость измеряемой цепи не превышает 1200 пФ.

При подключении приставки непосредственно к катушкам расположенным на плате применяется проводка длиной 30 сантиметров с зажимами для фиксации или щупами. Провода скручиваются с расчетом один виток на сантиметр длины. В таком случае образуется индуктивность приставки в диапазоне 0,5 – 0,6 мкГн, которую также необходимо учитывать при измерениях индуктивности.

Применение катушек в технике

Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:

• сглаживание пульсаций и помех, накопление энергии;
• создание магнитных полей в различных устройствах;
• фильтры цепей обратной связи;
• создание колебательных контуров;
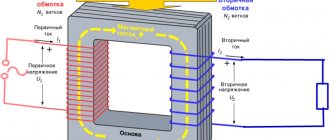
• трансформаторы (устройство из двух катушек, связанных индуктивно);
• силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
• ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
• применение катушек в качестве электромагнитов различных исполнительных механизмов;
• обмотки электромагнитных реле;
• индукционные печи;
• установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока. При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

Самоиндукция и измерение индуктивности

Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:

L = N х F : I.

Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.

Настройка измерителя индуктивности

Для того чтобы откалибровать приставку для измерения индуктивности понадобятся несколько индукционных катушек с известной индуктивность (например, 100 мкГн и 15 мкГн).

Катушки по очереди подключаются к приставке и, в зависимости от индуктивности, движком подстроечного резистора на экране мультиметра выставляется значение 100,0 для катушки на 100 мкГн и 15 для катушки на 15 мкГн с точностью 5%.

По такому же методу устройство настраивается и в других диапазонах. Важным фактором является то, что для точной калибровки приставки необходимы точные значение тестовых катушек индуктивности.

Альтернативным методом определения индуктивности является программа LIMP. Но этот способ требует некоторой подготовки и понимания работы программы.

Но как в первом, так и во втором случае точность подобных измерений индуктивности будет не очень высока. Для работы с высокоточным оборудованием данный измеритель индуктивности подходит плохо, а для домашних нужд или для радиолюбителей будет отличным помощником.

Индуктивное сопротивление – как его найти

Реальная катушка имеет не только реактивное, но и обычное сопротивление. Индуктивное сопротивление определяется по формуле:

XL=2*П*v*L

Здесь употреблены следующие обозначения:

1. XL – рассматриваемая величина.
2. Символом «П» обозначено число Пи.
3. V представляет собой частоту.
4. L — это обозначение величины индуктивности.

Надо отметить, что величина (2*П*v) представляют собой круговую частоту, которую обозначают греческим символом «омега».

Катушки с различными сердечниками

Рассматриваемая величина подчиняется закону Ома. Формула выглядит так:

I = U / XL

I, U представляют собой ток и напряжение, XL – это индуктивное сопротивление.

Конфигурация магнитного поля катушки

Для определения искомой величины можно воспользоваться приведенными формулами. При этом можно воспользоваться амперметром и вольтметром. Первый из них надо включить последовательно, второй — параллельно.

При этом необходимо учитывать следующее. На самом деле, в цепи, в которую включена индуктивность, действует два вида сопротивления: активное и реактивное. Измерив ток и напряжение, можно определить их результирующую величину. Нужно помнить, что она не является их простой суммой.

Дело в том, что в переменной цепи, где имеется только катушка и нет конденсатора, напряжение находится впереди тока на четверть периода колебания. Эта величина равна 90 градусам.

Полное сопротивление определяется следующим образом. Для этого необходимо нарисовать соответствующую диаграмму. Если по горизонтали отложить величину обычного, а по вертикали — реактивного, а затем по этим векторам построить прямоугольник, то длина его диагонали будет равна полному значению.

Магнитное поле провода

К примеру, если подобрать элементы цепи таким образом, чтобы по абсолютной величине обе этих величины были равны, то искомая часть определится как их полное значение, умноженное на квадратный корень из двух.

Для того, чтобы получить информацию о зависимости индуктивного сопротивления от частоты, возможно воспользоваться осциллографом.

При использовании переменного тока необходимо учитывать не только обычное, но и индуктивное сопротивление. Оно возникает в том случае, если в электрической цепи присутствует катушка.

Советуем изучить Все о плавких предохранителях

Последовательное соединение катушек индуктивности.

При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:

L_0 = L_1 + L_2

Вроде бы все просто, проще некуда, но тут есть один важный момент. Данная формула справедлива только в том случае, если катушки расположены на на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:

Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация совсем другая. Возможно два варианта:

• магнитные потоки катушек имеют одинаковое направление
• магнитные потоки направлены навстречу друг другу

Первый случай называется согласным включением катушек – начало второй катушки подключается к концу первой. А второй вариант называют встречным включением – конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом “*“. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:

L = L_1 + L_2 + 2M

Где M – взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:

L = L_1 + L_2\medspace-\medspace 2M

Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу – уменьшается на ту же самую величину.

Индуктивность, ее единица си. Индуктивность длинного соленоида.

Индукти́вность

(или
коэффициент самоиндукции
) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность , краем которой является этот контур. .

—магнитный поток, — ток в контуре, — индуктивность.

Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.

Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока :

.

Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током :

.

Как найти индуктивность проводника

Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф

B), индукция пропорциональна силе тока в проводнике (B

I), следовательно магнитный поток пропорционален силе тока (Ф

ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.

Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.

Также индуктивность можно рассчитать по формуле:

где Ф – магнитный поток через контур, I – сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды

Индуктивность взаимная – величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).

Магнитный поток Ф12 через контур 2, созданный током I1 в контуре 1, прямо пропорционален току:

Коэффициент пропорциональности M12 зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.

Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.

Колебательный контур

Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.

Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.

Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.

Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.

Расчет катушки индуктивности

При построении электронных устройств часто приходится сталкиваться с индуктивным элементом схемы. Когда на чертеже указано только значение индуктивности L, то расчет катушки индуктивности приходится выполнять самостоятельно. В интернете есть множество программ, позволяющих выполнять расчёт индуктивности катушек онлайн при помощи специального калькулятора. Зная то, как устроен элемент, можно вручную произвести все вычисления.

Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)

Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.

Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.

Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.

Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.

Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:

где:

• n — повое число витков катушки;
• n1 — число витков катушки, указанное в описании;
• d— диаметр имеющеюся провода;
• d1 — диаметр провода, указанный в описании.

В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:

(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).

Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:

При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.

Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.

Рис. 2. Катушки индуктивности. Пример.

Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.

Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.

Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:

Новая катушка на каркасе с увеличенным диаметром:

Ошибка при пересчете составляет 0,25 мкГн, что вполне допустимо для расчетов в радиолюбительской практике.

Катушки индуктивности

В. ПОЛЯКОВ, г. Москва

Любой проводник с током создает вокруг себя магнитное поле. Отношение магнитного потока этого поля к по-рождающему его току называется индуктивностью. Индуктивность прямого отрезка проводника невелика и составляет 1…2 мкГн на каждый метр длины в зависимости от диаметра провода (тонкие проводники имеют большую индуктивность). Более точные результаты дает формула L = 0,2ℓ(ln4ℓ/d — 1), где ℓ — длина провода; d — его диаметр. Оба размера надо брать в метрах (под знаком логарифма допустимо в любых, но одинаковых единицах), индуктивность получится в микрогенри. Для облегчения расчетов напомним, что натуральный логарифм любого числа в 2,3 раза больше десятичного логарифма (который можно найти с помощью таблиц, логарифмической линейки или калькулятора), т. е. lnx = 2,3lgx. Зачем мы дали эту формулу? Поясним примером. Пусть выводы некоторого радиоэлемента имеют длину 4 см при диаметре 0,4 мм. Сосчитаем их индуктивность. 2,3lg100 = 4,6 и 0,2∙0,04∙3,6 = 0,03 (округляем). Итак, индуктивность каждого вывода близка к 0,03 мкГн, а двух выводов — 0,06 мкГн. С емкостью всего 4,5 пФ (а емкость монтажа может быть и больше) такая индуктивность образует колебательный контур, настроенный на частоту 300 МГц, — вспомните формулу Томсона: f = 1/2π√LC. Вот почему на УКВ нельзя вести монтаж длинными проводами и оставлять длинные выводы деталей. Чтобы увеличить индуктивность, проводник сворачивают в кольцо. Магнитный поток внутри кольца возрастает, и индуктивность становится примерно втрое больше: L = 0,2πD(ln8D/d — 2). Здесь D — диаметр кольца, размерности те же. Дальнейшее увеличение индуктивности происходит при увеличении числа витков, при этом магнитные потоки отдельных витков не только складываются, но и воздействуют на все остальные витки. Поэтому индуктивность возрастает пропорционально квадрату числа витков. Если в катушке N витков, полученную для одного витка индуктивность надо умножить на N². Для однослойной цилиндрической катушки с длиной ℓ, намного большей диаметра D (рис. 23), индуктивность достаточно точно рассчитывается по формуле L = μμₒN²S/ℓ, строго выведенной для очень длинного соленоида или тора. Все размерности здесь в системе СИ (метры, Генри), μₒ = 4π∙10⁻⁷ Гн/м — магнитная константа; S = πD²/4 — площадь поперечного сечения катушки; μ — эффективная магнитная проницаемость магнитопровода. Для незамкнутых магнитопроводов она значительно меньше проницаемости самого материала. Например, для стержня магнитной антенны из феррита марки 600НН (магнитная проницаемость 600) μ едва достигает 150. Если магнитопровода нет, μ = 1.

Очень точные результаты эта формула дает для тороидальных катушек, причем ℓ соответствует длине окружности кольцевого магнитопровода, измеренной по его средней линии. Формула годится и для низкочастотных трансформаторов, намотанных на Ш-образном магнитопроводе (рис. 24). В этом случае S = ab — площадь сечения магнитопровода, а ℓ — это средняя длина магнитной силовой линии, показанная на рисунке пунктиром. Для замкнутых магнитопроводов, собранных без зазора, как и для ферритовых колец, μ берется равной магнитной проницаемости материала. Малый зазор незначительно снижает μ. Учесть его влияние можно, увеличив длину магнитной силовой линии ℓ на величину δμ, где δ — ширина зазора, μ — магнитная проницаемость материала сердечника. Как видим, от диаметра провода индуктивность практически не зависит. У низкочастотных катушек диаметр провода выбирают исходя из допустимой плотности тока, для медных проводников 2…3 ампера на каждый мм² сечения проводника. В других случаях, особенно у радиочастотных катушек, стремятся получить минимальное сопротивление проводника, чтобы увеличить добротность (отношение индуктивного сопротивления к активному).

С этой целью надо, казалось бы, увеличивать диаметр провода, но тогда увеличивается длина намотки, что снижает индуктивность, а при тесном, многослойном расположении витков наблюдается эффект «вытеснения» тока из обмотки, что увеличивает сопротивление. Эффект аналогичен вытеснению тока на высоких частотах в любых проводниках, в результате чего ток течет только в тонком скин-слое у поверхности проводника. Толщина скин-слоя уменьшается, а сопротивление провода растет пропорционально корню квадратному из частоты. Таким образом, для получения нужных индуктивности и добротности совсем не обязательно выбирать самый толстый провод. Например, если однослойную катушку (см. рис. 23) намотать толстым проводом виток к витку или вдвое более тонким проводом, но с шагом, равным диаметру провода, индуктивность останется прежней и добротность почти не уменьшится. Добротность возрастает при увеличении вместе с диаметром провода всех размеров катушки, главным образом, ее диаметра. Для получения максимальной добротности и индуктивности катушку выгоднее делать короткой, но большого диаметра, с отношением D/ℓ порядка 2,5. Индуктивность таких катушек более точно рассчитывается по эмпирической (подобранной опытным путем) формуле L = 0,1D²N²/(4D + 11ℓ). где размеры берутся в сантиметрах, а индуктивность получается в микрогенри. Любопытно, что эта же формула применима для спиральной или корзиночной плоской катушки (рис. 25).

В качестве D берут средний диаметр: D = (Dmax + Dmin)/2, а в качестве ℓ — ширину намотки, ℓ = (Dmax — Dmin)/2. Индуктивность многослойной катушки без сердечника (рис. 26) вычисляется по формуле L = 0,08D²N²/(3D + 9b + 10с), где размеры подставляются в сантиметрах, а индуктивность получается в микрогенри. При плотной рядовой намотке добротность не превосходит 30…50, «рыхлая» намотка (внавал, универсаль) дает большие значения добротности. Еще лучше «сотовая» намотка, теперь практически забытая. На частотах до 10 МГц добротность увеличивается при использовании литцендрата — провода, скрученного из многих тонких изолированных жилок. У литцендрата больше общая поверхность провода, по которой, собственно, и течет ток из-за скин-эффекта, а следовательно, меньше сопротивление на высокой частоте.

Подстроечник из магнитодиэлектрика увеличивает индуктивность вплоть до 2—3 раз, в зависимости от размеров подстроечника. Еще большее увеличение индуктивности дают замкнутые или частично замкнутые магнитопроводы, например, горшкообразные. В этом случае лучше пользоваться строгой формулой для соленоида или тора (см. выше). Добротность катушки на замкнутом магнитопроводе определяется не столько проводом, сколько потерями в материале сердечника. В заключение главы приведем несколько полезных формул для подсчета активного сопротивления проводов. Погонное сопротивление (на метр длины) медного провода на постоянном токе и низких частотах (Ом/м) легко найти по формуле R = 0,0223/d², где d — диаметр провода, мм Толщина скин-слоя для меди (мм) примерно равна 1/15√f (МГц). Обратите внимание: уже на частоте 1 МГц ток проникает в провод на глубину всего 0,07 мм! В случае, когда диаметр провода больше толщины скин-слоя, сопротивление возрастает по сравнению с сопротивлением на постоянном токе. Погонное сопротивление провода на высокой частоте оценивают по формуле R = √f/12d (мм). К сожалению, эти формулы нельзя использовать для определения активного сопротивления катушек, поскольку из-за эффекта близости витков оно получается еще больше. Настало время дать ответы на первые задачи, приведенные в предыдущих разделах. Задачка из введения («Радио», 2002, № 9, с. 52): какова длительность единичных импульсов (по отношению к периоду) на выходе логического элемента (рис. 2), если он переключается при напряжении 2 В, а на вход подан синусоидальный сигнал с амплитудой 4 В? Решать эту задачу проще и нагляднее графически — надо по возможности точнее нарисовать синусоиду амплитудой 4 В и провести прямую горизонтальную линию на уровне порога переключения элемента, т. е. 2 В (рис. 27).

Элемент будет переключаться в моменты времени, соответствующие точкам пересечения синусоиды с этой линией. Длительность получившихся импульсов (выделены утолщенными линиями) теперь можно измерить линейкой — она составит 1 /3 периода. По горизонтальной оси графика целесообразно отложить не время, а фазу колебания φ. Полный период составит 360°, а моменты переключения находятся из уравнения 4sinф = 2 или sinφ =1/2 (оно приравнивает мгновенное значение напряжения порогу переключения). Решения уравнения: ф = 30°, 150° и т. д. Разность фаз между моментами переключения составляет 150 — 30 = 120°, длительность импульса по отношению к периоду составит 120/360 = 1/3. Таким образом, задачку можно решить и алгебраически, но легко запутаться в многозначном решении уравнения для ф, поэтому нарисовать график оказалось очень полезно. Если даже не стараться рисовать график аккуратно, по нему получим приближенную оценку, а из решения алгебраического уравнения — точный результат. Теперь вторая задача, предложенная в конце первого раздела: Измерения батареи показали ЭДС 12 В и ток короткого замыкания 0,4 А. Какую взять лампочку, чтобы свет был как можно ярче? Определяем внутреннее сопротивление батареи: r = Е/Iкз = 12/0,4 = 30 Ом. Чтобы свет был максимально ярким, на лампочке фонаря должна выделяться максимальная мощность (не напряжение, и не ток, а именно мощность, преобразующаяся затем в тепло: Q = P∙t). Это происходит при равенстве сопротивления нагрузки внутреннему сопротивлению источника: R = r. Из всех перечисленных лампочек лишь одна удовлетворяет этому условию — находим ее сопротивление по закону Ома: 6 В/0,2 А = 30 Ом. Она и окажется самой яркой. Заметьте также, что на ней выделится напряжение 6 В и будет протекать ток 0,2 А, т. е. лампа будет светить в рекомендуемом для нее режиме.

Статья из журнала Радио 2003 № 1

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Советуем изучить Прибор для измерения силы

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Особенности расчёта индуктивных элементов с сердечниками

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.

Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения

где ω – количество витков катушки,

RM – сопротивление магнитной цепи,

μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,

SM – площадь поперечного сечения сердечника,

lM – длина средней магнитной силовой линии,

Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.

Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле

где ω – количество витков катушки,

μ0 – магнитная постоянная, μ0 = 4π*10-7,

μr – относительная магнитная проницаемость вещества,

Se – эффективная площадь поперечного сечения сердечника,

le – эффективный путь магнитной линии сердечника.

Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:

С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;

С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;

где N – количество разнородных участков сердечника,

lN – длина N – го участка сердечника,

SN – площадь N – го участка сердечника.

Тогда величины Se и le определятся из следующих выражений

Кроме индуктивности с помощью постоянных С1 и С­2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению

где ω – количество витков катушки,

μ0 – магнитная постоянная, μ0 = 4π*10-7,

μr – относительная магнитная проницаемость вещества,

С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.

Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.

Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.

В чем измеряется индуктивность катушки

Понятие индуктивности. Единицы измерения. Катушки индуктивности. (10+)

Индуктивность. Понятие. Единицы измерения

Материал является пояснением и дополнением к статье:

Единицы измерения физических величин в радиоэлектронике Единицы измерения и соотношения физических величин, применяемых в радиотехника.

В самом начале изучения электричества исследователи заметили, что мотки провода при подаче на них напряжения ведут себя странно. Сила тока через них не подчиняется классическому закону Ома. Электрический ток не возникает сразу после подачи напряжения, а нарастает постепенно со временем. Прекратить этот ток тоже непросто. При разрыве цепи возникает искра в месте разрыва. Создается впечатление, что электрический ток в мотке провода обладает инерцией. Теоретические изыскания подтвердили это наблюдение. В катушках индуктивности после подачи на них напряжения происходит накопление энергии в магнитном поле и постепенный рост электрического тока. Если внешний источник отключить, то катушка продолжает поддерживать на своих вывода напряжение достаточное для постепенного убывания силы тока по мере исчерпания накопленной энергии. Если в цепи разрыв, то скачек напряжения может быть очень большим. Теоретические он должен быть бесконечным, но на практике либо происходит пробой места разрыва или изоляции самой катушки, либо вся энергия поглощается паразитными емкостями между витками.

Если подключить катушку индуктивности к батарейке, а потом разорвать цепь, держа одной рукой за один контакт места разрыва, а другой рукой — за другой, то Вы получите ощутимый удар тока. Если катушка обладает большой индуктивности и хорошими параметрами, то Вас может даже убить, хотя вроде бы в Ваших руках обычная батарейка. Кстати на этом эффекте основана работа электрошокера.

Энергия катушки индуктивности.

Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину накопленной энергии катушки индуктивности:

W = \frac{LI^2}{2}

Давайте переходить к вариантам соединения катушек между собой… Все расчеты мы будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0 и его необходимо учитывать при проведении любых расчетов.

Добротность катушки

Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.

Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:

где:

• π – число пи, ≈3,14,
• f – частота,
• R – сопротивление.

Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает

Активное сопротивление и добротность катушки индуктивности.

Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.

Рассматривая примеры включения катушек в различные цепи мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:

Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:

U_L = IR_а

Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление будет равно:

X_L = 2\pi f L = 0

А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давай разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:

u = iR + u_L

Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:

u_L = -\varepsilon_L = L\frac{di}{dt}

И мы получаем для напряжения на реальной катушке индуктивности:

u = iR + L\frac{di}{dt}

Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:

Q = \frac{X_L}{R}

Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Итак, активное сопротивление катушки мы рассмотрели, давайте перейдем к следующему вопросу.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

B= µ0nI,

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

E = LI2 :2,

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Расчет

Вычислить число витков, зная конструкцию, можно по формуле нахождения энергии и ее магнитного поля W = LI2/2, где L является индукцией, I — силой тока. Витки находятся из формулы L/d, где d является проводным диаметром. Стоит указать, что есть специальный калькулятор, в который нужно только подставить необходимые параметры. При этом можно определить, однослойный или многослойный проводник.

Схематическое расположение витков в катушке

С сердечником

Стоит отметить, что со стержнем, намоткой, обмоткой индукция вычисляется через замкнутый магнитный поток индуктивных элементов, в то время как без него учитывается поток, который пронизывает только проводник с токовой энергией. Расчитывая индуктивность подобных элементов, необходимо учесть размеры и материал центральной части. Обобщенно можно представить формулу схематично. При этом требуется взять в расчет источник с сопротивлением магнитной цепи, абсолютной магнитной проницаемостью вещества, площадью поперечного сердечникового сечения и длиной средней силовой линии. Зная это, можно посчитать индукцию. Стоит учитывать погрешность. Она будет равна 25%.

Вам это будет интересно Определение резонанса

Расчет индуктивности катушки с сердечником

Без сердечника

Стоит указать, что без ферритового, геометрического и цилиндрического сердечника с мощным каркасом источник имеет небольшую индукцию, а с ним она повышается. Это связано с тем, что имеется материальная магнитная проницаемость. Форма бывает разная. Есть броневой, стержневой и тороидальный материал.

Обратите внимание! Рассчитать можно, используя метод эллиптических максвелловских интегралов и специальную онлайн программу.

Расчет индуктивности без сердечника

Катушка — незаменимый компонент любой электросети, который имеет вид скрученного или обвивающего элемента с проводником. Влияет на ее индукцию число проводных витков, площадь сечения, длина и материал сердечника. Отыскать количество витков и посчитать индуктивность с сердечником и без него несложно, главное — руководствоваться приведенными выше рекомендациями.