Свойства катушек индуктивности

Калькулятор расчета индуктивности прямого провода

На практике, самый обычный провод, используемый для питания различных потребителей электрической энергии, также обладает определенной индуктивностью. Разумеется, что размер индуктивности в таком случае несоизмерим с индуктивностью катушек, но в определенных ситуациях, эта величина может внести значительное влияние на работу высокоточных электронных приборов. А так как индуктивность представляет собой способность накапливать электрическую энергию, то в масштабах электрических сетей, такие накопления способны привести к некорректной работе силовых установок, задержке срабатывания защит, остаточному электричеству после отключения.
Разумеется, что индуктивность прямого провода для проводников в масштабах одной квартиры или шнура питания одного бытового прибора ничтожно мала. Так как величина индуктивности прямого провода прямо пропорциональна его длине. Но для линий с протяженностью в несколько километров, этот параметр приобретает значительные величины. Для вычисления индуктивности необходимо воспользоваться формулой:

L = 0.00508 * l * (log * (2 * l/D) — 0.75)

Где l – это длина провода, а D – его диаметр.

Данная величина может быть особо актуальной при расчете токов коротких замыканий в линиях электроснабжения. Которые необходимы для определения уставок срабатывания защит. Для расчета можно воспользоваться формулой, но извлечение логарифма предоставляет ряд неудобств. Поэтому гораздо удобнее воспользоваться онлайн калькулятором, который позволит определить индуктивность без лишних затрат времени и каких-либо сложных математических операций. Для этого вам достаточно указать длину и диаметр провода, а потом нажать на кнопку «Рассчитать».

Источник

Индуктивность коаксиального кабеля

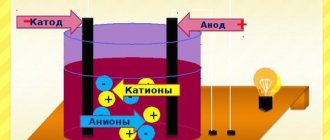
Коаксиальный кабель представляет собой два длинных соосных прово­дящих цилиндра, пространство между которыми заполнено каким-либо изолирующим материалом с магнитной проницаемостью m.

Пусть а — радиус внутреннего цилиндра, а b — внешнего. Длина кабеля обычно во много раз превышает его радиус. Поэтому магнитное поле, создава­емое электрическим током в кабеле, будет таким же как у бесконечно длинного кабеля, если не учитывать искажения поля у его концов.

Найдем индуктивность участка кабеля длиной l. Для этого создадим замкнутую электрическую цепь из внутреннего и внешнего цилиндров кабеля и подключим к этой цепи источник постоянной ЭДС (рис. 8.6, а).Токи, создаваемые этой ЭДС, потекут по поверхностям цилиндров вдоль их оси в противоположных направлениях.

В силу цилиндрической симметрии системы силовые линии магнит­ного поля суть семейство окружностей, центры которых лежат на оси симметрии. На рис. 8.6, а изображена одна из силовых линий. Для определения напряженности магнитного поля применим теорему (7.7) о циркуляции вектора Н .

В качестве контура интегрирования
С
выберем силовую линию произвольного радиуса г. Циркуляция вектора напря­женности по такому контуру буд

Hdl= H dl

=
H dl
=
Н 2pr
. (8.33)

H

Рис. 8.6. Коаксиальный кабель

Если радиус контура С

меньше радиуса внутреннего цилиндра (г <
а),
то внутри контура
С
ток не протекает. В случае, когда кон­тур
С
охватывает оба цилиндра (г > 6), сумма токов равна нулю, так как токи в цилиндрах имеют противоположные направления. Поэтому напряженность магнитного поля Я = 0 при
г < а
и
г > Ь,
т.е. магнитное поле внутри малого цилиндра и вне большого отсутствует. Если радиус контура
С
таков, что
а
< г <
Ь,
то такой контур охватывает только ток во внутреннем цилиндре. При этом по теореме (7.7) циркуляция (8.32) будет равна силе тока / в рассматриваемой цепи:

2prН = I.

Таким образом, напряженность магнитного поля внутри коаксиального кабеля

Н = I /2pr.

Плотность энергии магнитного поля в пространстве, где а

< r < b
,
найдем по формуле (8.28):

w = (1/2) mH2

= (1/2)
m I2 /8p2 r2.
(8.35)

Найдем энергию магнитного поля внутри кабеля. Для этого рассмо­трим цилиндрический слой, образованный двумя воображаемыми цилин­драми радиусов r и r + dr

(рис. 8.6, б).Если длина слоя равна l, то его объем
dV
=
2prldr.
Так как плотность энергии (8.35) зависит только от г, внутри тонкого цилиндрического слоя она будет всюду одна и та же. Поэтому энергия магнитного поля в слое

dW = w(r) dV =

(1/2)(
m I2 /
(
8p
2r2))2
prldr
.

Проинтегрировав это выражение по r в пределах от а

до
b,
найдем энер­гию магнитного поля на участке кабеля длиной l:

W =

(1/4
p
)
m I2l =
(1/4
p
)
m I2l
ln(b/a) (8.36)

С другой стороны, энергию магнитного поля можно определить по формуле (8.26). Приравняем эти выражения и найдем индуктивность участка коаксиального кабеля длиной l:

L= 2W/I2 =(1/2p

)
m l ln
(b/a) (8.37)

Взаимная индукция

Рассмотрим два контура с токами I1 и I2 (рис. 8.7), расположенные на некотором расстоянии друг от друга. Ток в первом контуре созда­ет магнитное поле, поток yкоторого через второй контур, очевидно, пропорционален силе тока I2

y2 = L21I1

(8-38)

Аналогично, магнитный поток Ф1 через первый контур поля, создавае­мого током во втором контуре, пропорционален силе тока I2.

y1 = L12I2

(8.39)

Коэффициенты пропорциональности L12

и
L21
называются
взаимной ин­дуктивностью,
или
коэффициентами взаимной индукции.
Они зависят от формы, размеров, взаимного расположения контуров и от магнитной проницаемости среды, в которой находятся контуры.

Рис. 8.7. Взаимная индукция

Рассмотрим простой пример. Пусть на одном цилиндрическом каркасе имеется две обмотки, образующие два соленоида одинаковой длины l(рис. 8.8). Число витков одного соленоида равно N1,

а второго —
N2.
Найдем коэффициенты
L12
и L21 для этой системы.

Рис. 8.8. К вычислению коэффициента взаимной индукции

редположим, что в первом соленоиде течет ток I1,

а во втором —
12.
В силу (7.17) напряженность магнитного поля тока
h
внутри соленоида

H1 = N1I1/l

Поток магнитной индукции этого поля через один из витков 2 соленоида

Ф2 = B1S =

m N1I1S/l

Так как поле внутри соленоида однородно, потоки через все витки оди­наковы. Поэтому потокосцепление

y2 = N2 Ф2 = B1S =

m N1
N2
I1S/l

L21=

m N1
N2
S/l

Аналогично, напряженность поля, создаваемого током I2, будет

Н2 = N2I2/l

Поток магнитной индукции этого поля через один из витков первого соленоида

Ф1 = B2S =

m N2I2S/l

Ф1 =

y2 = N1 Ф1 =

m N1
N2
I2S/l

Отсюда найдем, что

L21 = L12

(8.41)

Это равенство справедливо для двух любых контуров и составляет со­держание теоремы взаимности.

Вычислим энергию магнитного поля двух соосных соленоидов. Векто­ры напряженности полей, создаваемых токами I1

и I2, внутри соленоидов коллинеарны. Если токи
I1
и I2 текут в одном направлении, то векто­ры
H1
и
Н2
сонаправлены. В этом случае суммарное магнитное поле характеризуется напряженностью:

H = H1

+
Н2 =
(
N1I1 + N2I2
)/l (8.40)

Если же токи I1 и I2 текут в разных направлениях, то векторы Н1

и
H2 направлены противоположно друг другу. При этом модуль напряженно­сти магнитного поля
H =

|
H1
+
Н2
|
=
|
H1
—
Н2
|
=
(
N1I1 — N2 I2
)/l

Энергию однородного магнитного поля найдем по формуле (8.28):

W = (1/2) mH2V=

(1/2)
m
(
N1I1 ± N2 I2
)2V/
l2
При помощи формул (8.22) и (8.40), запишем это выражение так:

W

= (1/2)
L1I1
2 +(1/2)
L2 I2
2
± L12I1 I2
где первое слагаемое есть энергия тока в первом соленоиде, второе -энергия тока во втором, а третье слагаемое называется взаимной энерги­ей.

Формула (8.42) справедлива в общем случае для двух произвольных контуров.

Задача. Найти взаимную индуктивность тороидальной катушки и проходящего по ее оси бесконечного прямого провода. Катушка имеет прямоугольное сечение. Внутренний радиус тороида равен а,

внешний —
b,
а его высота —
h.
Число витков в катушке —
N.
Магнитная проницае­мость окружающей среды —
m.

Расчет катушки индуктивности

При построении электронных устройств часто приходится сталкиваться с индуктивным элементом схемы. Когда на чертеже указано только значение индуктивности L, то расчет катушки индуктивности приходится выполнять самостоятельно. В интернете есть множество программ, позволяющих выполнять расчёт индуктивности катушек онлайн при помощи специального калькулятора. Зная то, как устроен элемент, можно вручную произвести все вычисления.

Применение

Микрополосковая линия представляет собой плоский проводник, отделенный диэлектриком от большой проводящей плоскости земли. Применение микрополосковых линий обусловлено тем, что на очень высоких частотах необходимые значения индуктивности и емкости были очень малы для обычных катушек индуктивности и конденсаторов. Таким образом, микрополосковые линии выполняют те же функции, что и катушки индуктивности и конденсаторы, только на сверхвысоких частотах. Они используются в качестве подстроечных цепей, схем согласования импедансов, фильтров, фазовращателей и реактивных компонентов.

Что такое катушка индуктивности

Данный элемент ещё называют дросселем. Это свёрнутый в спираль изолированный провод. Для такой спирали характерны большие индуктивные и маленькие ёмкостные параметры.

Важно! Дроссель препятствует протеканию переменного тока, потому что обладает существенной инерционностью. Она препятствует любому изменению проходящего через витки тока. При этом нет разницы, увеличивается он или уменьшается.

В связи с этим данные элементы применяют в электротехнике для осуществления:

• токоограничения;
• ослабления биений;
• помехоподавления;
• формирования магнитного поля;
• изготовления датчиков движения.

Дроссель входит в систему колебательного контура в цепях резонанса и применяется в линиях задержки.

ИНДУКТИВНОСТЬ

Индуктивность цепи характеризуется отношением магнитного по­тока Ф к току I

, создавшему этот поток:

Индуктивность кабелей.измеряют и нормируют в генри, милли­генри (10–3 гн)

и микрогенри (10–6
гн)
на 1
км
или 1
м.
Индуктивность одножильного кабеля, а также внешняя индук­тивность коаксиального кабеля

Индуктивность коаксиального кабеля

Общая индуктивность коаксиального кабеля с медными внутрен­ним и внешним проводниками

В случае многопроволочного внутреннего проводника его диаметр

Индуктивность внутреннего проводника спирального радиоча­стотного кабеля задержки, выполненного в виде спирали поверх сер­дечника с магнитной проницаемостью μ c,

Индуктивность двухжильного неэкранированного кабеля (рис. 2-4)

Индуктивность двухжильного экранированного кабеля (рис. 2-5)

Индуктивность двухжильного кабеля с учетом магнитного пото­ка внутри жил:

где Q (x) — коэффициент, зависящий от коэффициента вихревых токов,

и радиуса жилы (табл. 2-2). С возрастанием частоты передаваемого тока общая индуктивность цепи уменьшается, а внешняя индуктивность не зависит от частоты.

Индуктивность двухпроводной линии (рис. 2-4), когда μ =1,

Индуктивность одиночного провода

При больших сечениях жил, а также при высоких частотах про­исходит уплотнение тока у периферии жилы, благодаря чему снижа­ется напряженность магнитного поля внутри жилы. С учетом этого на практике для определения индуктивности одиночного провода пользуются формулой

Конструкция катушки

По конструктивному исполнению индуктивные элементы различаются:

• видом намотки: винтоспиральная, винтовая; кольцевая;
• количеством слоёв: однослойные или многослойные;
• типом изолированного провода: одножильный, многожильный;
• наличием каркаса: каркасные или бескаркасные (при небольшом количестве витков толстого провода);
• геометрией каркаса: прямоугольный, квадратный, тороидальный;
• наличием сердечника: ферритовый, из карбонильного железа, электротехнической стали, пермаллоевый (магнитомягкий сплав), металлический (латунный);
• геометрией сердечника: стержневой (разомкнутый), кольцо-образный или ш-образный (замкнутый);
• возможностью изменять L в узких интервалах (движение сердечника по отношению к обмотке).

Существуют плоские катушки, в печатном исполнении устанавливаемые на платах цифровых устройств.

К сведению. Намотка провода может быть как рядовой (витком к витку), так и в навал. Последний способ укладки провода снижает паразитную ёмкость.

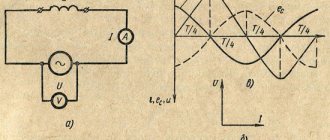
Индуктивность в цепи переменного тока

Для опытов с постоянным током катушка индуктивности намотана тонким проводом с большим количеством витков. Это делается для того, чтобы при подаче на нее напряжения с мощного источника питания витки катушки не перегорели, т.к. при намотке витков толстым проводом сопротивление будет маленьким, а ток через нее большой (по закону Ома для постоянного тока I=U/R) и она может сгореть. Сопротивление катушки индуктивности постоянному току (которое можно измерить мультиметром) называется активным сопротивлением.

Расчет параметров катушки

Приходится при расчётах рассматривать разные варианты. Расчет индуктивности зависит от исходных данных и заданных конечных параметров.

Расчет L в зависимости от заданной конструкции

Если исходными параметрами являются: w, D каркаса и длина намотанного провода, то формула для расчёта имеет вид:

L = 0,01*D*w2/(l/D) + 0,46,

где:

• D – диаметр каркаса, см;
• w – число витков;
• l – длина намотки, см;
• L – индуктивность, мкГн.

Эквивалентная схема реальной катушки индуктивности

Каждый дроссель можно представить в виде эквивалентной схемы.

Данная схема состоит из элементов:

• Rw – сопротивление обмотки с выводами;
• L – индуктивность;
• Cw – паразитная ёмкость;
• Rl – сопротивление потерь.

Изготавливая индуктивный элемент, стремятся снизить величину сопротивления потерь, паразитную ёмкость. При работе катушки на низкой частоте учитывают сопротивление её обмотки Rw. На таких частотах действуют токи большой величины.

Правильно рассчитанная катушка индуктивности будет иметь высокую добротность (180-300) и стабильность работы при влиянии внешних условий (температуры и влажности). Зная способы различной намотки и манипуляции с шагом, можно уменьшить влияние паразитных факторов.