Тесла — единица измерения магнитной индукции в системе СИ
Единица магнитной индукции ($\overline{B}$) в международной системе единиц (СИ) называется тесла (Тл), по имени сербского ученого Н. Тесла, который успешно работал в области радиотехники и электроники.
Единицу измерения магнитной индукции определим исходя из закона Ампера. Рассмотрим прямолинейный проводник, длиной $l$ по которому течет ток $I$. Пусть этот проводник находится в однородном магнитном поле $\overline{B}$, причем вектор индукции поля перпендикулярен проводнику. В таком случае модуль силы Ампера (${\overline{F}}_A$), воздействующей на проводник равен:
\[F=IBl\ \left(1\right).\]
Выразим магнитную индукцию из формулы (1), получим:
\[B=\frac{F}{I\cdot l}\left(2\right).\]
Из выражения (2) мы видим, что тесла (единица измерения магнитной индукции) — это величина, соответствующая магнитной индукции однородного магнитного поля, действующего на каждый метр прямого проводника, находящегося в магнитном поле перпендикулярно направлению $\overline{B}$, с силой в один ньютон, при силе тока в проводнике в один ампер:
\[\left[B\right]=Тл=\frac{H}{A\cdot м}.\]
Единица измерения магнитной индукции (тесла) является производной в системе Международных единиц (СИ). Через основные единицы СИ Тл, как единицу измерения магнитной индукции выражают, учитывая, что:
\[Н=\frac{кг\cdot м}{с^2},\]
тогда получаем:
\[\left[B\right]=Тл=\frac{кг\cdot м}{с^2}\cdot \frac{1}{A\cdot м}=\frac{кг}{А\cdot с^2}.\]
Стандартные приставки системы СИ можно использовать с Тл при обозначении десятичных кратных и дольных единиц. Например, $кТл$ (кило тесла), $1кТл=1000Тл$; нТл (нано тесла), $1нТл={10}^{-9}Тл.$
1 Тл — достаточно большая величина магнитной индукции, особенно, если речь идет о постоянном магнитном поле. Человек на сегодняшний день смог создать постоянное магнитное поле величиной 100,75 Тл. Искусственно созданное людьми импульсное магнитное поле достигло величины индукции в $2,8\cdot {10}^3Тл$. Магнитное поле Земли может существенно отличаться в зависимости от местоположения на планете, оно составляет порядка $\approx $10 мкТл.
Физический смысл магнитной индукции
Прежде, чем перейти к рассмотрению формулы магнитной индукции, нужно выяснить, чем объясняется возникновение самого явления в системе. Соленоид не является плоским элементом и включает в себя спираль из проводника (металла). При отсутствии воздействующих на него магнитных явлений находящиеся в кристаллической решетке материала спирали электрозаряды ведут себя статично. Когда в соленоиде движется постоянный магнитный элемент, формирующий поле, под его влиянием движутся и заряженные частицы, тогда в индуктивном элементе появляется электрический ток, сила которого определяется характеристиками магнитного и спирального элемента и тем, как быстро происходит движение.
Важно! Имеющие одинаковую ориентацию поля суммируются, образуя общее поле. Когда передвижение заряженных частиц в соленоиде прекращается, сердечник перестает проявлять магнитные характеристики, если он выполнен из мягкого металла (к стальным изделиям это правило не относится).
Магнитный поток
Для характеристики воздействия индукционного фона на контур из металла используют такую величину, как поток. Она является скалярной. В контексте этого необходимо узнать, индукция в чем измеряется. Она зависит от количества идущих через единицу сечения проводящего элемента силовых линий. В международной системе СИ за измерительную единицу принимается Тесла (Тл). Отсюда и название устройства, предназначенного для замеров – теслометра. 1 Тл – индукция, возникающая в полевом пространстве, в котором момент силы в 1 Н*м оказывает воздействие на контур площадью 1 квадратный метр, по которому течет ток в 1 ампер.
Магнитный поток
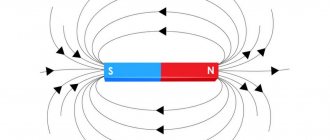
Магнитное поле
Под данным термином в физике подразумевается некое силовое поле, оказывающее определённое влияние на перемещающиеся заряженные частицы, и на прочие тела, имеющие определённый магнитный момент. Воздействие оказывается не зависимо от того, находятся ли эти частицы в состоянии покоя, либо же в движении. Кроме вектора магнитной индукции, дополнительной характеристикой поля выступает векторный потенциал. Он носит альтернативный характер, но при этом, в физическом смысле, неразрывно связан с магнитной индукцией.
Для поля, действующего в абсолютном вакууме, главной характеристикой обычно выбирается не индукция, а его напряжённость, обозначаемая Н. Однако, подобная замена в сфере действия земного магнитного поля уже не имеет особого смысла, в связи с чем, в практических опытных измерениях и наблюдениях за основную характеристику магнитного поля всё же принимается вектор магнитной индукции.
Фактически, магнитное поле допустимо определить, как особую материю, с помощью которой происходит взаимодействие меж некими заряженными элементарными частицами, передвигающимися с определённой скоростью.
При этом не стоит путать магнитную и электромагнитную индукцию. Под электромагнитной индукцией понимается закономерность, установленная англичанином М. Фарадеем. Суть закономерности состоит в возникновении электромагнитного силового поля под действием переменного электротока, протекающего в замкнутом проводниковом контуре. В контуре возникает определённая движущая сила, в свою очередь, порождающая индукционный ток. Магнитное поле, наряду с электрическим полем, выступает как одна из двух частей электромагнитного поля.
Теория о постоянных магнитах, своим воздействием вызывающих возникновение индукции, была разработана французским физиком А-М. Ампером, в честь него позднее была названа единица мощности электротока. Он впервые установил, что движения электронов вокруг центра атома в итоге порождают микроскопические, или элементарные магнитные поля. Также им был открыто свойство металлических проводников сохранять магнитные свойства некоторое время после прекращения воздействия на них магнитным полем.
Источник
Индукция магнитного поля. Магнитная индукция.
Магнитная индукция () — это векторная физическая величина, характеризующий магнитное поле. За направление вектора магнитной индукции
принимается:
1. направление от южного полюса S к северному полюсу N магнитной стрелки, свободно устанавливающейся в магнитном поле, или
2. направление положительной нормали к замкнутому контуру с током на гибком подвесе, свободно устанавливающемся в магнитном поле. Положительной считается нормаль, направленная в сторону перемещения острия буравчика (с правой нарезкой), рукоятку которого вращают по направлению тока в рамке.
Ясно, что направления 1) и 2) совпадают, что было установлено еще опытами Ампера.
Что касается величины магнитной индукции (т. е. ее модуля) В, которая могла бы характеризовать силу действия поля, то экспериментами было установлено, что максимальная сила F, с которой ноле действует на проводник с током (помещенный перпендикулярно линиям индукции магнитного поля), зависит от силы тока I в проводнике и от его длины Δl (пропорциональна им). Однако сила, действующая на элемент тока (единичной длины и силы тока), зависит только от самого поля, т. е. отношение для данного поля является величиной постоянной (аналогично отношению силы к заряду для электрического поля). Эту величину и определяют как магнитную индукцию:
.
Индукция магнитного поля в данной точке равна отношению максимальной силы, действующей на проводник с током, к длине проводника и силе тока в проводнике, помещенном в эту точку.
Чем больше магнитная индукция в данной точке поля, тем с большей силой будет действовать поле в этой точке на магнитную стрелку или движущийся электрический заряд.
Единицей магнитной индукции в СИ является тесла (Тл), названная в честь хорватского электротехника Николы Теслы. Как видно из формулы, .
Источник
Тесла, как единица измерения:
Тесла – единица измерения плотности магнитного потока, напряжённости и индукции магнитного поля в Международной системе единиц (СИ), названная в честь изобретателя Николы Теслы.
Тесла как единица измерения имеет русское обозначение – Тл и международное обозначение – T.
1 тесла равен индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 ампер действует сила 1 ньютон. Другими словами, один тесла равен напряжённости поля, действующего на проводник с силой один ньютон на метр проводника при силе тока на каждый ампер тока.
Аналогично, один тесла представляет собой плотность магнитного потока в один вебер на квадратный метр площади.
Тл = кг / (с2 · А) = Н / (А · м) = Вб / м2.
1 Тл = 1 кг / (1 с2 · 1 А) = 1 Н / (1 А · 1 м) = 1 Вб / 1 м2.
В Международную систему единиц тесла введён решением XI Генеральной конференцией по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом. В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы «тесла» пишется со строчной буквы, а её обозначение — с заглавной (Тл). Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием теслы.
Линии магнитной индукции
Сама индукция магнитного поля характеризуется определенным направлением, представляющим собой линии, отображаемые графически. Эти линии, также получили название магнитных линий, или линий магнитных полей. Так же, как и магнитная индукция, ее линии имеют собственное определение. Они представляют собой линии, к которым проведены касательные во всех точках поля. Эти касательные и вектор магнитной индукции совпадают между собой.
Однородное магнитное поле отличается параллельными линиями магнитной индукции, совпадающими с направлением вектора во всех точках.
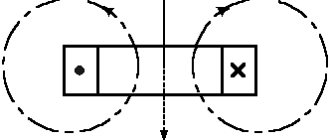
Если же магнитное поле является неоднородным, произойдет изменение вектора электромагнитной индукции в каждой пространственной точке, расположенной вокруг проводника. Касательные, проведенные к этому вектору, приведут к созданию концентрических окружностей вокруг проводника. Таким образом, в данном случае, линии индукции будут выглядеть в виде расширяющихся окружностей.
Величина модуля вектора магнитной индукции
Экспериментируя с поведением рамки с током в магнитном поле, можно обнаружить, что момент сил, действующих на нее, существенно зависит от следующих факторов:
- от величины магнитного поля;
- от площади рамки;
- от тока, проходящего по рамке;
- от магнитных свойств вещества самой рамки и среды вокруг нее;
- от ориентации рамки в магнитном поле.
Таким образом, формула модуля вектора магнитной индукции должна учитывать все эти факторы. Фактор ориентации рамки удобно исключить из выражения, условившись рассматривать только такую ориентацию, при которой момент сил, действующих на рамку, будет максимальным. Для исключения магнитного влияния в веществе рамки и вокруг нее, будем рассматривать только рамку в вакууме.
В результате в левой части формулы будет стоять искомый модуль, а в правой — выражение, включающее момент сил, действующих на рамку, площадь рамки и силу тока в ней.
Очевидно, что вектор магнитной индукции прямо пропорционален моменту сил, действующих на рамку.
С площадью рамки и током в ней ситуация обратная. Если увеличивать эти величины, то при неизменном магнитном поле момент сил будет пропорционально увеличиваться. А значит, индукция магнитного поля обратно пропорциональна как площади рамки, так и току, проходящему по ней.
Окончательно имеем формулу модуля вектора магнитной индукции:
$$B = k {M_{max} \over IS}$$
где:
- $В$ — модуль вектора магнитной индукции;
- $M_{max}$ — максимальный момент, действующий на рамку с током;
- $I$ — ток в рамке с током;
- $S$ — площадь рамки с током;
- $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц измерения.
Рис. 3. Магнитная индукция.
Зависимость магнитной индукции
На электромагнитную индукцию абсолютно не влияют, ни сила тока, ни длина проводника. Она находится в прямой зависимости и связи, только с магнитным полем. Таким образом, при уменьшении силы тока в проводнике, без изменения каких-либо других показателей, происходит уменьшение не индукции, прямо пропорционально связанной с силой тока, а той силы, с которой магнитное поле воздействует на проводник. При этом, значение самой магнитной индукции остается постоянным. Благодаря этим качествам, электромагнитная индукция выступает в роли количественной характеристики магнитного поля.
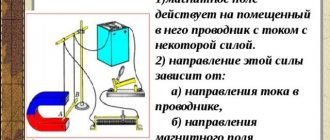
Измерение магнитной индукции производится в теслах, по формуле: 1 Тл=1 Н/(А*м). Физическую зависимость этой величины от различных факторов, можно определить в ходе проведения несложного эксперимента. Необходимо взять весы, где на одной стороне прикрепляется проводник, а на другой стороне расположены гири. Проводник находится в постоянном электромагнитном поле, при этом, его масса и вес гирь имеют одинаковое значение.
После уравновешивания весов, по проводнику пропускается электрический ток. Вокруг него происходит образование магнитного поля, определяемое в соответствии с правилом правой руки. В результате, наблюдается взаимодействие полей постоянного магнита и самого проводника. При этом, равновесие весов будет нарушено. Из-за протекания тока, сторона весов с проводником начинает опускаться. Для того, чтобы вычислить силу воздействия поля на этот проводник, нужно уравновесить его с помощью гирь. Сила их тяжести рассчитывается по специальной формуле, и будет равняться силе магнитного поля, воздействующей на проводник с током. Соотношение этой силы с длиной проводника и силой тока является постоянной величиной. Данная количественная характеристика находится в зависимости только от поля и представляет собой ни что иное, как модуль вектора магнитной индукции.
Магнитная индукция
Из курса физики в 11 классе известно, что проявление магнитного поля состоит в возникновении силы, действующей на проводник с током в этом магнитном поле.
Рис. 1. Проводник с током в магнитном поле.
Таким образом, для характеристики интенсивности магнитного поля целесообразно ввести специальную силовую характеристику — магнитную индукцию.
Как правило, силовая характеристика поля показывает силу, с которой это поле действует на единичный пробный заряд в этом поле. Сила — величина векторная, значит, и магнитная индукция также будет векторной.
Направление вектора магнитной индукции определяется по правилу буравчика или по правилу обхвата правой руки (это эквивалентные правила, но правило правой руки нагляднее и удобнее):
Рис. 2. Правило правой руки.
При определении модуля вектора магнитной индукции существует две проблемы.
- Магнитных зарядов не обнаружено (хотя теория не запрещает их существование). Однако, согласно закону Ампера, магнитное поле действует на проводник с током. Следовательно, в качестве пробного заряда в магнитном поле необходимо брать такой проводник.
- Направление возникающей силы не совпадает с направлением тока. Поэтому необходимо использовать рамку с током, в которой существуют токи, направленные в противоположные стороны, и за основу силовой характеристики брать не силу, а момент сил, действующих на эту рамку.
Учитывая эти особенности магнитного поля, можно найти модуль вектора магнитной индукции.
Магнитная индукция в системе «Сантиметр-Грамм-Секунда»
В системе СГС связь индукции и напряженности в присутствии магнитного материала определяется следующим соотношением:
B=H+4πI
В этой формуле I — магнитный момент единицы объема материала (намагниченность). В системе СГС для измерения этой величины используются Гауссы (Гс).
Индукция характеризует поле, возникающее в веществе. Напряженность определяет параметры внешних магнитных полей и магнитных полей в вакууме. Величина B также может использоваться для внешних магнитных полей.
В вакууме значения индукции и напряженности равны (по системе СГС).
Вектор магнитной индукции
Линии магнитной индукции
Все физические параметры делятся на две группы:
- Скалярные. Это такие величины, которые не имеют направления: вес, объём, электрическое напряжение или ток;
- Векторные. Это параметры, имеющие направление: скорость, ускорение или инерция.
Магнитная индукция – это векторная величина. Её направленность совпадает с касательной к линиям поля. Форма и направление линий индукции зависят от проводника.
Направление магнитной индукции
В прямом проводнике поле имеет форму кругов, перпендикулярно которых проходит этот проводник, а его центр совпадает с ними. Чем ближе к центру, тем больше силовых линий проходит через точку пространства и сильнее поле. Его направление определяется по правилу правой руки.
Правило правой руки
Если провод свернуть в кольцо, то поле приобретает форму тора (бублика). Если витков много, и длина превышает диаметр катушки, то внутри неё силовые линии идут равномерно и параллельно. Магнитные свойства этого прибора аналогичны постоянному магниту. Если обмотку намотать на сердечник, изготовленный из материала с высокой магнитопроницаемостью, то получится электромагнит, форма которого зависит от сердечника: плоский, квадратный или подковообразный. Направление магнитного поля, идущего через такие устройства, можно найти по правилу буравчика.
Правило буравчика
Модуль вектора
Вектор, кроме величины, имеет модуль, или размер, – это показатель, характеризующий численное значение параметра. Если сама магнитная индукция обозначается В, направленность – B→, то модуль обозначается |B|. Этот параметр зависит от тока и расстояния до проводника. Для определения модуля выражение имеет вид |В|=k*(I/r), где:
- k – коэффициент. Он зависит от конкретных условий. В катушке с магнитопроницаемым сердечником и большим количеством витков коэффициент больше, чем в прямом отрезке провода;
- I – сила тока. Чем она больше, тем сильнее создаваемое им поле и больше величина вектора;
- r – расстояние от места измерения до катушки или проводника. Чем ближе к магниту, тем плотнее расположены силовые линии, и больше модуль.
Рядом расположенные провода или катушки с электротоком влияют друг на друга. Сила этого взаимодействия находится по формуле:
F=|B|*I*l, где l – длина проводов.
Если эту формулу преобразовать по законам алгебры, чтобы определить вектор магнитной индукции, она примет следующий вид:
|B|=(F/(I*l).
С её помощью можно рассчитать величину вектора, зная силу взаимного влияния, силу тока и длину проводов.
Интересно. Это взаимодействие можно увидеть при изменении силы сварочного тока в проходящих рядом кабелях.
Что такое индуктивность
Этим термином обозначают зависимость, которая устанавливается между силой тока в проводнике (I) и созданным магнитным потоком (Ф):
L = Ф/ I.
С учетом базового определения несложно понять зависимость индуктивности от свойств окружающей среды, оказывающей влияние на распределение силовых линий. Определенное значение имеют размеры и конфигурация проводящего элемента.
Индуктивность подобна механической инерции. Только в данном случае речь идет о действиях с электрическими величинами. Этим коэффициентом характеризуют способность рассматриваемого компонента противодействовать изменению проходящего через него тока.