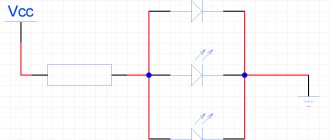
Соединение резисторов — это взаимное расположение данных элементов в цепи относительно друг друга и источника питания. Можно по отдельности выделить последовательное и параллельное соединение резисторов. Когда в схеме присутствуют оба варианта, то такое соединение называется смешанным.
Нам известно, что резистор — это электронный компонент, который обладает электрическим сопротивлением и мощностью рассеивания. Если в цепи имеется несколько резисторов, то для получения общего сопротивления прибегают к расчетам по правилам последовательного или параллельного соединения. Помимо общего сопротивления, группы резисторов по закону Ома влияют на напряжение и силу тока на участках цепи. И в данном обзоре будет доступно рассмотрена методика расчета общего сопротивления при различных видах соединения резисторов. Также будет рассмотрен наглядный пример со смешанным соединением резисторов, где помимо сопротивлений будут просчитаны напряжения и сила тока на разных участках.
Стоит сразу отметить, что в данной теме рассеивающая мощность резисторов вынесена за скобки. Мощность важна при подборе и комбинировании резисторов в схеме, но это уже отдельная тема. К тому же все рассмотренные примеры взяты с учетом источника переменного напряжения 220 В. Почему так? Об этом вы узнаете в последнем пункте публикации.
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
R = R1 + R2 + R3 + … + Rn.
R = 20 + 70 + 10 = 100 Ом.
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
I = U / R = U / (R1 + R2 + R3 + … + Rn).
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
- U1 = I × R1.
- U2 = I × R2.
- U3 = I × R3.
- Un = I × Rn.
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
R ≈ 1 / 0,164 ≈ 6,097 Ом.
Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):
Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Решение задач по теме:
Под соединением проводников подразумевается соединение резисторов – приборов, сделанных на основе сопротивления проводников. На предыдущих уроках были рассмотрены параллельное и последовательное соединения. На данном уроке будут рассмотрены задачи на смешанное соединение проводников, то есть когда в цепи присутствует и последовательное, и параллельное соединение.
Для решения задач сначала рассмотрим формулы для связи различных величин при параллельном и последовательном соединениях:
Если проводники соединены последовательно, то сила тока в них одинакова и равна силе тока в цепи. При этом общее напряжение в цепи будет состоять из суммы напряжений на каждом проводнике. А если говорить о сопротивлении этого участка цепи, в котором проводники соединены последовательно, то оно равно сумме сопротивлений проводников.
В последовательном соединении все по-другому. Сила тока в каждой ветке этой цепи будет различной, при этом общая сила тока в цепи будет вычисляться как сумма сил токов в проводниках. Напряжение на проводниках, соединенных последовательно, будет одинаковым. Общее сопротивление этого участка цепи, так называемое «эквивалентное сопротивление» R, будет вычисляться по следующей формуле: .
Также стоит отметить, что параллельное соединение обычно применяется при включении бытовых приборов, а последовательное – для того, чтобы создать длинную неразветвленную цепь.
Задача №1
Рассмотрим следующую задачу. Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Необходимо определить силу тока во всей электрической цепи (рис. 1).
Рис. 1. Условия и рисунок задачи № 1
Как видим, резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним. Источник дает напряжение 2,4 В, соответственно, на участке АВ напряжение будет также 2,4 В. Сила тока, которую требуется найти, – это сила тока, протекающая через амперметр А.
Такое соединение проводников называется неразветвленным. В промышленности обычно изготавливается набор резисторов с четко определенными сопротивлениями, но для экспериментов могут понадобиться любые различные сопротивления. Тогда с помощью таких схем можно создавать нужное сопротивление для эксперимента или прибора.
Далее требуется определить эквивалентное сопротивление неразветвленной части. Сначала посмотрим, чему равно сопротивление R’ участка цепи АВ, который содержит только резисторы R1 и R2. Они соединены последовательно, тогда R′=R1+R2=2 [Ом]. Теперь можно перерисовать электрическую цепь, заменив сопротивления R1 и R2 эквивалентным им сопротивлением R’ (рис. 2).
Рис. 2. Первая замена эквивалентным сопротивлением
Теперь можно сказать, что участок АВ включает в себя не три, а два сопротивления: R3 и R’. Эти два сопротивления соединены параллельно, соответственно, можно найти общее сопротивление электрической цепи по формуле . Выразив R и подставив значения , получаем:
Стоит отметить, что сопротивления были соединены, но общее сопротивление получилось все равно равным 1 Ом. Теперь электрическую цепь можно заменить следующей (рис. 3):
Рис. 3. Вторая замена эквивалентным сопротивлением
На рис. 3 сопротивление R=1 Ом называется эквивалентным сопротивлением, поскольку три сопротивления были заменены на одно. Чтобы рассчитать силу тока в цепи, надо использовать закон Ома для участка цепи: . Напряжение на сопротивлении R – это напряжение на участке АВ (Рис. 1), которое, в свою очередь, равно 2,4.Тогда . Это и будет значение силы тока в электрической цепи, которое покажет амперметр.
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
| Определяется общее сопротивление участков с параллельным соединением резисторов. | |
| Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление. | |
| После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений. | |
| Далее рассчитывается сопротивление полученной простой схемы. |