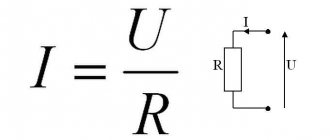Сопротивление
Сила тока в проводнике зависит не только от напряжения электрического поля в нём. Она зависит ещё от самого проводника: от его формы, размеров, от того, из какого материала он сделан. При одном и том же напряжении поля токи в разных проводниках будут различными.
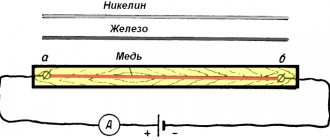
Возьмём кусок медной проволоки длиной в 100 метров с поперечным сечением в 4 квадратных миллиметра. Создадим на концах её напряжение в один вольт. Амперметр покажет в этом случае силу тока в 2,2 ампера.
При том же напряжении, в таком же куске железной проволоки ток будет равен только 0,44 ампера, а в такой же проволоке, но сделанной из нихрома (сплав никеля, железа и хрома) — всего лишь 0,03 ампера.
Медь, железо и нихром обладают различным электрическим сопротивлением. Сопротивление меди мало, железа — больше, а нихрома — очень велико.
Сопротивление зависит не только от материала проводника, но и от формы и размеров его. У толстой проволоки сопротивление меньше, чем у тонкой, у длинной — больше, чем у короткой. Чтобы понять, почему это так, надо выяснить, чем вызвано сопротивление проводников электрическому току. Об этом мы расскажем дальше.
За единицу сопротивления принято сопротивление такого проводника, в котором напряжение в один вольт создаёт ток в один ампер. Такое сопротивление называется один ом.
Итак, сила тока в проводнике зависит от напряжения поля на концах его и от сопротивления проводника. Чем больше напряжение, тем больше сила тока. Чем больше сопротивление, тем сила тока меньше.
Чтобы узнать, какова сила тока, надо разделить напряжение, созданное полем на концах проводника, на сопротивление этого проводника.
На практике силу тока обычно не вычисляют, а измеряют амперметром. Напряжение тоже измеряют. А зная напряжение и силу тока, не трудно уже вычислить сопротивление проводника.
Так как напряжение сила т о к а = напряжение /сопротивление, ТО
сопротивление = напряжение / сила т о к а ,
На зажимах дугового фонаря, изображённого на рис. 12, создано напряжение в 55 вольт. Через дугу идёт ток в 5 ампер. Значит, сопротивление горящей дуги равно
55 / 5 = 11 Ом.
Электрическим сопротивлением обладают не только металлы, но и все другие тела.
Особенно велико сопротивление изоляторов (кварц, резина, стекло, фарфор и др.). Если бы в изоляторах абсолютно не было свободных зарядов (электронов, ионов), то сопротивление их было бы бесконечным. Самое высокое напряжение не вызывало бы в изоляторах тока.
На самом деле таких идеальных изоляторов не существует. В любом изоляторе имеется небольшое число оторвавшихся от своих мест электронов и ионов. Поэтому и в изоляторах при наложении поля возникает ток.
Преимущества и недостатки термометров сопротивления
Преимущества термометров сопротивления
- Высокая точность измерений (обычно лучше ±1 °C), может доходить до 13 тысячных °C (0,013).
- Возможность исключения влияния изменения сопротивления линий связи на результат измерения при использовании 3- или 4-проводной схемы измерений.
- Практически линейная характеристика.
Недостатки термометров сопротивления
- Относительно малый диапазон измерений (по сравнению с термопарами)
- Дороговизна (в сравнении с термопарами из неблагородных металлов, для платиновых термометров сопротивления типа ТСП).
- Требуется дополнительный источник питания для задания тока через датчик.
Советуем изучить Индуктивное сопротивление
Виды и свойства полупроводников
Все полупроводники можно разделить на несколько основных видов. Среди них лидируют чистые или собственные материалы, в которых отсутствуют какие-либо примеси.
Для них характерна кристаллическая структура, где атомы расположены в периодическом порядке в ее узлах. Здесь существует устойчивая взаимная связь каждого атома с четырьмя атомами, расположенными рядом. Это дает возможность образовывать постоянные электронные оболочки, в состав которых входит восемь электронов. При температуре, равной абсолютному нулю, такой полупроводник становится диэлектриком, поскольку все электроны соединены ковалентными связями. Когда температура повышается или происходит какое-либо облучение, электроны могут выйти из ковалентных связей и превратиться в свободных носителей зарядов. Свободные места при перемещении постепенно занимаются другими электронами, поэтому электрический ток протекает только в одном направлении.
В электронных полупроводниках, кроме четырех атомов, составляющих основу кристаллической решетки, имеются так называемые доноры. Они представляют собой примеси в виде пятивалентных атомов. Электрон, содержащийся в таком атоме, не может нормально вступить в ковалентную связь и поэтому отделяется от донора. Таким образом, он превращается в свободный носитель заряда. В свою очередь донор становится положительным ионом, это может произойти даже при комнатной температуре.
В дырочных полупроводниках имеется кристаллическая решетка с содержанием трехвалентных примесных атомов, называемых акцепторами. В такой решетке остается незаполненной одна ковалентная связь. Она может быть заполнена электроном, оторвавшимся от соседней связи. Происходит превращение примесного атома в отрицательный ион, а на месте ушедшего электрона появляется дырка.То есть, в этом случае также начинается одностороннее движение электрического тока.
Факторы, влияющие на сопротивление полупроводников
Опытным путем было установлено, что при повышении температуры происходит уменьшение электрического сопротивления в полупроводниковых кристаллах. Это связано с тем, что при нагревании кристалла увеличивается количество свободных электронов, соответственно, возрастает их концентрация. Изменяющееся сопротивление полупроводников под воздействием температуры, применяется для создания специальных приборов, называемых терморезисторами.
Для того, чтобы изготовить терморезистор используются полупроводники, представляющие собой оксиды отдельных металлов в смешанном состоянии. Готовое вещество размещается в защитном металлическом корпусе с изолированными выводами. С их помощью происходит подключение прибора к электрической цепи.
Терморезисторы используются для измерения температуры или для ее поддержания в заданном режиме в каких-либо устройствах. Основным принципом их работы является изменяющееся сопротивление при перепадах температур. Тот же принцип используется и в фоторезисторах. Здесь величина сопротивления изменяется в зависимости от уровня освещения.
Принцип действия термометра сопротивления
Термометры сопротивления могут использоваться для измерения температуры электрическим путем, так как существует прямо пропорциональная зависимость между изменениями сопротивления и изменением температуры.
Другими словами, при повышении температуры величина сопротивления возрастает прямо пропорционально, а при понижении температуры сопротивление пропорционально уменьшается. Подобный принцип используется в термометрах сопротивления, так как сопротивление термометра уменьшается или увеличивается пропорционально температуре процесса, который он измеряет. Любое изменение сопротивления может быть зарегистрировано и преобразовано в температурные показания с помощью таблицы, или отображено на шкале, которая откалибрована в единицах измерения температуры.
Как и термопара или любой другой температурный датчик термометр сопротивления (RTD) функционален при измерении температуре только, если он подсоединен к электрической цепи. Обычно с термометрами сопротивления применяются мостовые схемы, так как такие схемы позволяют добиться высокой точности. Вместе с мостовой схемой используется батарея, которая служит в качестве источника питания. Цепи термометров сопротивления должны иметь внешний источник питания, так как они не способны генерировать напряжение сами.
Мостовая схема термометра сопротивления с батареей
Мостовая схема, изображенная на рисунке выше состоит из пяти резисторов: Р1, R2, R3, R4, R5; и точек соединения: А, В, С, D.
В данном случае давайте предположим, что каждый резистор в мостовой схеме обладает одинаковым сопротивлением. Так как ток протекает от минуса к плюсу в данном контуре, то протекание начинается с минусовой клеммы батареи и ток достигает точки А. В точке А ток расщепляется на равные части: одна половина протекает через сопротивление R1 в точку В, а другая половина протекает через R2 к точке С. Так как сопротивление всех резисторов одинаковое, то между точками В и С нет разницы в величине напряжения, поэтому ток через R5 не протекает.
Когда ток через средний резистор не протекает, то мост, как говорится «уравновешен». В данном примере ток протекает от точки В, через R3 в точку D. Ток также протекает от точки С через R4 в точку D. Ток от точки D возвращается на положительную клемму батареи, завершая цепь.
Протекание тока через уравновешенный мост
Мостовая схема, изображенная на рисунке выше похожа на предыдущую схему за исключением того, что резистор R3 заменен термометром сопротивления. В данной конфигурации ток по-прежнему протекает от минусовой клеммы батареи на точки В и С. Однако, если сопротивление термометра сопротивления (RTD) отличается по величине от сопротивления резистора R4, то между точками В и С появится напряжение. Это означает, что мост неуравновешен и ток будет протекать через резистор R5.
Мостовая схема с термометром сопротивления
Ток, протекающий через мост, может быть измерен, если мы заменим R5 измерительным прибором, который и будет определять температуру, измеряя ток. Так схема обеспечивает высокую точность, то она часто используется вместе с термометрами сопротивления для измерения температуры.
Мостовая схема с термометром сопротивления и измерительным прибором
Когда для измерения температуры используются термометры сопротивления, то они включаются в схему, подобно той, что показана на рисунке выше. Во многих случаях термометры сопротивления расположены на удалении от остальных элементов цепи, так как они подвержены воздействию температуры технологического процесса. По мере того, как температура вокруг термометра меняется, то пропорционально меняется величина сопротивления термометра. Когда сопротивление термометра меняется, то мост становится неуравновешенным и определенный ток протекает через измерительный прибор. Этот ток пропорционален изменениям температуры. Температура процесса затем может быть определена по показаниям шкалы прибора. В некоторых случаях шкалы откалиброваны на показания величины сопротивления, а не температуры. В таких случаях надо воспользоваться переводной таблицей для перевода ом в градусы.
Советуем изучить Ток короткого замыкания
Как повысить силу электрического тока. Сопротивление проводников. Удельное сопротивление
Закон Ома является самым главным в электротехнике. Именно поэтому электрики говорят: «- Кто не знает Закон Ома, пусть сидит дома». Согласно этому закону ток прямо пропорционален напряжению и обратно пропорционален сопротивлению ( I = U / R ), где R является коэффициентом, которое связывает напряжение и силу тока.
Единица измерения напряжения – Вольт, сопротивления – Ом, силы тока – Ампер.
Для того, чтобы показать, как работает Закон Ома, разберем простую электрическую цепь. Цепью является резистор, он же – нагрузка. Для регистрации на нем напряжения используется вольтметр. Для тока нагрузки – амперметр. При замыкании ключа ток идет через нагрузку. Смотрим, насколько соблюдается Закон Ома. Ток в цепи равен: напряжение цепи 2 Вольта и сопротивление цепи 2 Ома ( I = 2 В / 2 Ом =1 А). Амперметр столько и показывает. Резистор является нагрузкой, сопротивлением 2 Ома. Когда замыкаем ключ S1, ток течет через нагрузку. С помощью амперметра измеряем ток цепи. С помощью вольтметра – напряжение на зажимах нагрузки. Ток в цепи равен: 2 Вольта / 2 Ом = 1 А. Как видно это соблюдается.
Теперь разберемся, что нужно сделать, чтобы поднять силу тока в цепи. Для начала увеличиваем напряжение. Сделаем батарею не 2 В, а 12 В. Вольтметр будет показывать 12 В. Что будет показывать амперметр? 12 В/ 2 Ом = 6 А. То есть, повысив напряжение на нагрузке в 6 раз, получили повышение силы тока в 6 раз.
Рассмотрим еще один способ, как поднять ток в цепи. Можно уменьшить сопротивление – вместо нагрузки 2 Ом, возьмем 1 Ом. Что получаем: 2 Вольта / 1 Ом = 2 А. То есть, уменьшив сопротивление нагрузки в 2 раза, увеличили ток в 2 раза. Для того, чтобы легко запомнить формулу Закона Ома придумали треугольник Ома: Как можно по этому треугольнику определять ток? I = U / R. Все выглядит достаточно наглядно. С помощью треугольника также можно написать производные от Закона Ома формулы: R = U / I; U = I * R. Главное запомнить, что напряжение находится в вершине треугольника.
В 18 веке, когда был открыт закон, атомная физика находилась в зачаточном состоянии. Поэтому Георг Ом считал, что проводник представляет собой что-то, похожее на трубу, в которой течет жидкость. Только жидкость в виде электротока. При этом он обнаружил закономерность, что сопротивление проводника становится значительнее при увеличении его длины и меньше при увеличении диаметра.
Исходя из этого, Георг Ом вывел формулу: R = p *l / S,
где p – это некоторый коэффициент, умноженный на длину проводника и деленный на площадь сечения. Этот коэффициент был назван удельным сопротивлением, характеризующим способность создавать препятствие протеканию эл.тока, и зависит из какого материала изготовлен проводник. Причем, чем больше удельное сопротивление, тем больше сопротивление проводника. Чтобы увеличить сопротивление необходимо увеличить длину проводника, либо уменьшить его диаметр, либо выбрать материал с большим значением данного параметра. В частности, для меди удельное сопротивление составляет 0,017 ( Ом * мм2 / м ).
Подключение термометров сопротивления в электрическую измерительную схему
Используется 3 схемы включения датчика в измерительную цепь:
Схема подключения терморезистора по двухпроводной схеме.
2-проводная.
В схеме подключения простейшего термометра сопротивления используется два провода. Такая схема используется там, где не требуется высокой точности измерения. Точность измерения снижается за счёт сопротивления соединительных проводов, суммирующегося с собственным сопротивлением термометра и приводит к появлению дополнительной погрешности. Такая схема не применяется для термометров классов А и АА.
3-проводная.
Эта схема обеспечивает значительно более точные измерения за счёт того, что появляется возможность измерить в отдельном опыте сопротивление подводящих проводов и учесть их влияние на точность измерения сопротивления датчика.
Советуем изучить ПОТ РМ 016 2001 (Правила охраны труда)
4-проводная.
Является наиболее точной схемой измерения, обеспечивающей полное исключение влияния на результат измерения подводящих проводов. При этом по двум проводникам подается ток на терморезистор, а два других, в которых ток равен нулю, используются для измерения напряжения на нём. Недостаток такого решения — увеличение объёма используемых проводов, стоимости и габаритов изделия. Эту схему Невозможно использовать в четырехплечем мосте Уитстона.
В промышленности наиболее распространенной является трёхпроводная схема. Для точных и эталонных измерений используется только четырёхпроводная схема.
Электрическое сопротивление проводника
Электрическое сопротивление — физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику. Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки.
Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе, благодаря закону Джоуля-Ленца – Q=I2Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Удельное сопротивление
Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м . Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле
где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
| Вещество | p, Ом*мм2/2 | α,10-3 1/K |
| Алюминий | 0.0271 | 3.8 |
| Вольфрам | 0.055 | 4.2 |
| Железо | 0.098 | 6 |
| Золото | 0.023 | 4 |
| Латунь | 0.025-0.06 | 1 |
| Манганин | 0.42-0.48 | 0,002-0,05 |
| Медь | 0.0175 | 4.1 |
| Никель | 0.1 | 2.7 |
| Константан | 0.44-0.52 | 0.02 |
| Нихром | 1.1 | 0.15 |
| Серебро | 0.016 | 4 |
| Цинк | 0.059 | 2.7 |
Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
Влияние температуры на удельное сопротивление
Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле
где r – это удельное сопротивление после нагрева, r0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t2 – температура до нагрева, t1 — температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм2/м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2, после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.
Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.
На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор. Резистор применяется практически в любой электрической схеме.
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
\(~\rho_t = \rho_0 (1 + \alpha t) ,\) \(~R_t = R_0 (1 + \alpha t) ,\)
где ρ
0,
ρ
t — удельные сопротивления вещества проводника соответственно при 0 °С и
t
°C;
R
0,
R
t — сопротивления проводника при 0 °С и
t
°С,
α
— температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К-1). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент
сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
\(~\mathcal h \alpha \mathcal i = \frac{1 \cdot \Delta \rho}{\rho \Delta T} ,\)
где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ
.
Для всех металлических проводников α
> 0 и слабо изменяется с изменением температуры. У чистых металлов
α
= 1/273 К-1. У металлов концентрация свободных носителей зарядов (электронов)
n
= const и увеличение
ρ
происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α
< 0, например, для 10%-ного раствора поваренной соли
α
= -0,02 К-1. Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ
и
R
от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором
α
= const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
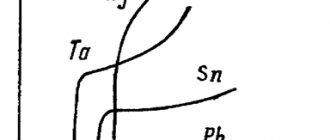
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
Рис. 1
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости
. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Металлы
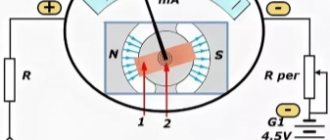
Как температура влияет на металлы? Чтобы узнать эту зависимость был проведен такой эксперимент: батарейку, амперметр, проволоку и горелку соединяют между собой с помощью проводов. Затем необходимо замерить показание тока в цепи. После того как показания были сняты, нужно горелку поднести к проволоке и нагреть ее. При нагревании проволоки видно, что сопротивление возрастает, а проводимость металла уменьшается.
где:
- Металлическая проволока
- Батарея
- Амперметр
Также нужно уделить внимание такому свойству, как сверхпроводимость. Если условия окружающей среды обычные, то охлаждаясь, проводники уменьшают свое сопротивление. График ниже показывает, как зависит температура и удельное сопротивление в ртути.
Сверхпроводимость – это явление, которое возникает, когда материалом достигается критическая температура (по Кельвину ближе к нулю), при которой сопротивление резко уменьшается до нуля.
Чем отличается термосопротивление от термопары
Принцип действия ТС объясняется изменением проводимости контрольного участка цепи. Термопара, несмотря на схожее название, функционирует по-другому. Изделия этой категории создают из двух разных материалов. Соединение (рабочую спайку) помещают в зону измерений. Колебания температуры провоцируют изменение потенциалов на выходах. Эти показания фиксируют вольтметром или другим подходящим прибором.
Принцип действия, функциональные компоненты термопары и способы измерения
К сведению. Приведенные сведения объясняют главные практические отличия датчиков разного рода. Термопара фактически является генератором ЭДС, поэтому дополнительный источник тока не нужен.
Термопарный преобразователь можно применить для измерения вакуума. Для этого обеспечивают контакт чувствительного участка с нитью лампы накаливания. Колбу соединяют трубкой с рабочей зоной. Изменение разряжения газа сопровождается увеличением (уменьшением) ЭДС. После калибровки шкалы достаточно точно можно определять значение контролируемого параметра.
Как температура влияет на металлы? Чтобы узнать эту зависимость был проведен такой эксперимент: батарейку, амперметр, проволоку и горелку соединяют между собой с помощью проводов. Затем необходимо замерить показание тока в цепи. После того как показания были сняты, нужно горелку поднести к проволоке и нагреть ее. При нагревании проволоки видно, что сопротивление возрастает, а проводимость металла уменьшается.
где:
- Металлическая проволока
- Батарея
- Амперметр
Зависимость указывается и обосновывается формулами:
Из этих формул следует, что R проводника определяется по формуле:
Пример зависимости сопротивления металлов от температуры предоставлен на видео:
Также нужно уделить внимание такому свойству, как сверхпроводимость. Если условия окружающей среды обычные, то охлаждаясь, проводники уменьшают свое сопротивление
График ниже показывает, как зависит температура и удельное сопротивление в ртути.
Сверхпроводимость – это явление, которое возникает, когда материалом достигается критическая температура (по Кельвину ближе к нулю), при которой сопротивление резко уменьшается до нуля.
Роль проводника тока
Если к веществу или материалу обладающему проводящей способностью, подключить источник ЭДС, то по нему начинает протекать электрический ток. Свободные электроны вещества при этом начинают направленное движение от отрицательного полюса к положительному, т.к они являются носителями отрицательного заряда.
Во время направленного движения электроны ударяются об атомы материала и передают им некоторую часть своей энергии, из-за этого происходит нагрев проводника по которому проходит ток. А электроны после столкновения замедляют свое движение. Но электрическое поле их опять ускоряет, поэтому они продолжают свое направленное движение к плюсу.
Этот процесс может идти практически бесконечно, пока вокруг проводника имеется электрическое поле созданное источником электродвижущей силы. Получается, что чем больше препятствий попадется на пути следования электронов, тем выше значение сопротивления.
В различных веществах имеется разное количество свободных электронов, а атомы, между которыми свободные носители заряда перемещаются, обладают различным местом расположения. Поэтому сопр. проводников току зависит, в первую очередь от материала, из которого они сделаны, от площади и длины поперечного сечения.
Если сравнить два проводника сделанные из одинакового материала, то более длинный имеет большее R при равных площадях поперечных сечений, а с большим поперечным сечением имеет более низкое сопр. при равных длинах. Рассмотрим практический пример: Подключим лампочку накаливания на 60Вт в розетку с сетевым напряжением. Спираль лампочки начинает создавать потоку электронов с потенциалом в 220В некоторое препятствие.
Если эта преграда на пути электронов окажется слишком маленькой лампочка перегорит. Если слишком большое – накальная нить будет гореть очень слабо. А вот если оно будет “оптимальное, тогда лампочка будет гореть нормально, выделяя при этом и тепло. Вырабатываемое тепло называют “потерянной” энергией, так как часть энергию затрагивается на никому ненужный нагрев.
Что такое электрическое удельное сопротивление? Из формулы закона Ома можно записать, что электрическое сопротивление является физической величиной, которую можно вычислить как отношение напряжения в проводнике к силе протекающего в нем тока.
Итак, исходя из опыта с лампочкой чуть выше можно сделать вывод, что электрическое сопротивление проводника является физической величиной, которая указывает на свойство вещества преобразовывать электрическую энергию в тепловую.
(R= ρ × l)/S
ρ — удельное сопротивление материала проводника, Ом·м, l — длина, м, и S — площадь сечения, м2. Удельное электрическое сопротивление является также физической величиной, которая равна сопротивлению метрового проводника с площадью сечения в один метр квадратный. На практике, сечение измеряют в квадратных миллиметрах.
Сопротивление различных металлов
Поэтому и удельное электрическое сопротивление проще считать в Ом × мм2 / м, а площадь подставлять в мм2. Формула выше говорит о том, что удельное сопр. прямо пропорционально удельному сопр. материала, из которого он сделан, а также его длине и обратно пропорционально площади поперечного сечения проводника.
Сопр. проводников зависит также от температуры. Так у элементов из металла с повышением температуры R увеличивается. Зависимость эта сложная, но в относительно узких пределах температурного изменения (примерно до 200° Цельсия) можно условно считать, что для каждого металла существует определенный, так называемый температурный, коэффициент сопротивления (альфа), который выражает определенный прирост сопротивления дельта r при изменении температуры на один градус цельсия, отнесенный к 1 ом начального значения сопротивления. Таким образом, температурный коэффициент удельного сопротивления будет равен α = r2-r1/r1(T2-T1) и прирост сопр. будет равен Δr=r2-r1=αr2(T2-T1)
Например, у медного линейного провода при температуре T1 = 15° r1 = 50 ом, а при температуре T2 = 75° — r2 — 62 ом. Поэтому, дельта при изменении температуры на 75 — 15 = 60° будет равно 62 — 50 = 12 ом. Т.е, дельта, соответствующий изменению температуры на 1°, равен: 12/60=0,2 От чего зависит удельное сопротивление.
Во-первых, от материала проводника. Чем больше значение ρ, тем хуже будет пропускная токовая способность. Во-вторых, от длины провода – с увеличением длины сопротивление увеличивается. В-третьих, от толщины. У более толстого проводника, более низкое сопротивление. И в-четвертых, от температуры проводника.
Если он из металла, то их удельное сопротивление возрастает с ростом температуры. В исключение можно поместить специальные сплавы – их электрическое удельное сопр. практически не изменяется при нагревании. Например: никелин, константан и манганин. А вот у жидкостей с нагревом, удельное сопротивление уменьшается.
Связь с удельной проводимостью в изотропных материалах, выражется формулой: ρ = 1 / σ Где σ – удельная проводимость. Явление сверхпроводимости Предположим температуру материала будем уменьшать, то удельное сопротивление при этом будет также снижаться. Есть предел, до которого можно снизить температуру – абсолютный нуль.
Проводник в разрезе
В численном выражении равен —273°С. Ниже этого значения температур просто не существует. При этом значении удельное сопротивление любого проводника будет равно нулю. так как при абсолютном нуле атомы кристаллической решетки полностью перестают колебаться. В результате электронное облако проходит между узлами решетки, не соударяясь с ними. Удельное сопр. материала становится равным нулю, что открывает возможности для получения бесконечно огромных токовых уровней в проводниках малого сечения. Явление сверхпроводимости открывает фантастические перспективы для развития электротехники и электронной техники. Но пока еще имеются некоторые сложности, связанные с получением в быту сверхмалых температурных значений, требуемых для создания нужного эффекта. Когда эти проблемы смогут преодолеть, электротехника шагнет на принципиально новый уровень развития.
Газы
Газы выполняют роль диэлектрика и не могут проводить электроток. А для того чтобы он сформировался необходимы носители зарядов. В их роли выступают ионы, и они возникают за счет влияния внешних факторов.
Зависимость можно рассмотреть на примере. Для опыта используется такая же конструкция, что и в предыдущем опыте, только проводники заменяются металлическими пластинами. Между ними должно быть небольшое пространство. Амперметр должен указывать на отсутствие тока. При помещении горелки между пластинами, прибор укажет ток, который проходит через газовую среду.
Ниже предоставлен график вольт-амперной характеристики газового разряда, где видно, что рост ионизации на первоначальном этапе возрастает, затем зависимость тока от напряжения остается неизменная (то есть при росте напряжения ток остается прежний) и резкий рост силы тока, который приводит к пробою диэлектрического слоя.
Рассмотрим проводимость газов на практике. Прохождение электрического тока в газах применяется в люминесцентных светильниках и лампах. В этом случае катод и анод, два электрода размещают в колбе, внутри которой есть инертный газ. Как зависит такое явление от газа? Когда лампа включается, две нити накала разогреваются, и создается термоэлектронная эмиссия. Внутри колба покрывается люминофором, который излучает свет, который мы видим. Как зависит ртуть от люминофора? Пары ртути при бомбардировании их электронами образуют инфракрасное излучение, которое в свою очередь излучает свет.
Если приложить напряжение между катодом и анодом, то возникает проводимость газов.
Законы физики и ток в жидкостях
Электричество в наших домах и технике, как правило, не передается в металлических проволоках,. В металле электроны могут переходить от атома к атому, и, таким образом нести отрицательный заряд.
Как жидкости, они приводятся в виде электрического напряжения, известного как напряжение, изменяемом в единицах – вольт, в честь итальянского ученого Алессандро Вольта.
Видео: Электрический ток в жидкостях: полная теория
Также, электрический ток течет от высокого напряжения в низкое напряжение и измеряется в единицах, известных как ампер, названных по имени Андре-Мари Ампера. И согласно теории и формулы, если увеличить напряжение тока, то его сила также увеличится пропорционально. Это соотношение известно как закон Ома. Как пример, виртуальная ампермерная характеристика ниже.
Рисунок: зависимость тока от напряжения
Закон Ома (с дополнительными подробностями относительно длины и толщины проволоки), как правило, является одним из первых вещей, преподаваемых в классах, изучающих физику, многие студенты и преподаватели поэтому рассматривают электрический ток в газах и жидкостях как основной закон в физике.
Высоколегированные стали
Высоколегированные стали имеют удельное электрическое сопротивление в несколько раз выше чем углеродистые и низколегированные. По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10-8 Ом·м.
При температуре 1300°С сопротивление высоко- и низко- легированных сталей становится почти одинаковым и не превышает 131·10-8 Ом·м.
Удельное электрическое сопротивление высоколегированных сталей ρэ·108, Ом·м
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
| Г13 | 68,3 | 75,6 | 93,1 | 95,2 | 114,7 | 123,8 | 127 | 130,8 |
| Г20Х12Ф | 72,3 | 79,2 | 91,2 | 101,5 | 109,2 | — | — | — |
| Г21Х15Т | — | 82,4 | 95,6 | 104,5 | 112 | 119,2 | — | — |
| Х13Н13К10 | — | 90 | 100,8 | 109,6 | 115,4 | 119,6 | — | — |
| Х19Н10К47 | — | 90,5 | 98,6 | 105,2 | 110,8 | — | — | — |
| Р18 | 41,9 | 47,2 | 62,7 | 81,5 | 103,7 | 117,3 | 123,6 | 128,1 |
| ЭХ12 | 31 | 36 | 53 | 75 | 97 | 119 | — | — |
| 40Х10С2М (ЭИ107) | 86 | 91 | 101 | 112 | 122 | — | — | — |
Жидкости
Проводники тока в жидкости – это анионы и катионы, которые движутся за счет электрического внешнего поля. Электроны обеспечивают незначительную проводимость. Рассмотрим зависимость сопротивления от температуры в жидкостях.
где:
- Электролит
- Батарея
- Амперметр
Зависимость воздействия электролитов от нагревания прописывает формула:
Где а – отрицательный температурный коэффициент.
Как зависит R от нагрева (t) показано на графике ниже:
Такая зависимость должна учитываться, когда осуществляется зарядка аккумуляторов и батарей.
Задание
Воздушная трехпроводная линия длиной L выполнена проводом, марка которого дана в таблице 2.1. Необходимо найти величину, обозначенную знаком «?», используя приведенный пример и выбрав по таблице 2.1 вариант с указанными в нем данными.
Следует учесть, что в задаче, в отличие от примера, предусмотрены расчеты, связанные с одним проводом линии. В марках неизолированных проводов буква указывает на материал провода (А – алюминий; М – медь), а число – сечение провода в мм
| Длина линии L, км | Марка провода | Температура провода Т, °С | Сопротивление провода RТпри температуре Т, Ом |
Изучение материала темы завершается работой с тестами № 2 (ТОЭ-
ЭТМ/ПМ» и № 3 (ТОЭ – ЭТМ/ ИМ)
Возрастает кинетическая энергия атомов и ионов, они начинают сильнее колебаться около положений равновесия, электронам не хватает места для свободного движения.
Как зависит удельное сопротивление проводника от его температуры? В каких единицах измеряется температурный коэффициент сопротивления?
Удельное сопротивление проводников линейно возрастает с увеличением температуры по закону.
Чем можно объяснить линейную зависимость удельного сопротивления проводника от температуры?
Удельное сопротивление проводника линейно зависит от частоты столкновений электронов с атомами и ионами кристаллической решетки, а эта частота зависит от температуры.
Почему удельное сопротивление полупроводников уменьшается при увеличении температуры?
При увеличении температуры возрастает число свободных электронов, а так как возрастает количество носителей заряда, то сопротивление полупроводника уменьшается.
Зависимость сопротивления от температуры
«Всё это так не потому что я такой умный.
Это всё из-за того, что я долго
не сдаюсь при решении задач»
Альберт Эйнштейн
Данная тема посвящена решению задач на зависимость сопротивления проводника от температуры
Задача 1.
Найдите сопротивление алюминиевого провода длиной 20 м и площадью поперечного сечения 2 мм2 при температуре 70 ºС, учитывая то, что в таблице указаны значения удельных сопротивлений при температуре 20 ºС.
| ДАНО: | РЕШЕНИЕ Зависимость удельного сопротивления от температуры имеет вид Тогда при температуре 70 ºС Сопротивление проводника можно определить по формуле Тогда при температуре 70 ºС |
Ответ
: 0,32 Ом.
Задача 2.
На баллоне лампы накаливания написано 220 В, 100 Вт. Когда нить накала была холодной, т.е. комнатной температуры, на неё подали напряжение 2 В и измерили силу тока. Ток оказался равен 50 мА. Найдите приблизительно температуру накала, нити, учитывая то, что она сделана из вольфрама.
| ДАНО: | СИ | РЕШЕНИЕ Из формулы для определения мощности электрического тока определим сопротивление Запишем закон Ома для участка цепи Тогда Запишем зависимость сопротивления от температуры Запишем выражение для сопротивления при некоторой температуре t 1 Тогда отношение сопротивлений Выразим из данной формулы температуру t Значения сопротивлений при температурах t и Тогда |
Ответ:
приблизительная температура накала нити 2462 ºС.
Задача 3.
Медный провод нагревается под действием электрического тока от 0 до 25 ºС за 3 мин. Через провод протекает ток 50 А. Предполагая, что изменение силы тока незначительно, найдите работу тока при нагревании провода. Сопротивление провода при 0 ºС равно 200 мОм.
| ДАНО: | СИ | РЕШЕНИЕ Работа электрического тока рассчитывается по формуле Мощность электрического тока Начальное сопротивление – это сопротивление при нуле градусах Чтобы вычислить сопротивление при 25 ºС, необходимо записать зависимость сопротивления от температуры Вычислим мощность тока при 0 и 25 ºС Как видно из формулы, мощность линейно зависит от сопротивления, а сопротивление, в свою очередь, линейно зависит от температуры. Поэтому, мощность будет линейно зависеть от температуры. Чтобы найти работу тока, необходимо построить график зависимости мощности от времени. Чтобы найти работу тока, необходимо найти площадь под графиком. Площадь трапеции равна Тогда работа |
Ответ
: 94,5 кДж.
Задача 4.
К концам проволоки приложено некоторое напряжение. По мере нагревания проволоки до 50 ºС, сила тока уменьшилась от 1 до 0,9 А. Найдите начальную температуру проволоки, если её температурный коэффициент сопротивления равен 0,004 ºС–1.
| ДАНО: | РЕШЕНИЕ Запишем закон Ома для участка цепи Исходя из данного закона запишем сопротивление проволоки при начальной и конечной температурах Отношение этих сопротивлений равно Зависимость сопротивления от температуры Тогда для начальной и конечной температуры сопротивления равня Отношения этих сопротивлений Приравняем две формулы выражающие отношения сопротивлений Из последней формулы выразим начальную температуру |
Ответ:
20 ºС
Задача 5.
Две одинаковые проволоки подключены параллельно. Одна из этих проволок помещена в тающий лёд, а другая находится при температуре 20 ºС. Температурный коэффициент сопротивления проволок равен 0,01 ºС–1. Сравните общее сопротивление этого участка с сопротивлением, которое было бы, если бы обе проволоки находились при температуре 20 ºС.
| ДАНО: | РЕШЕНИЕ Зависимость сопротивления от температуры имеет вид Тогда при температурах 0 ºС и 20 ºС При параллельном соединении Если две одинаковые проволоки находятся при одной и той же температуре, то их сопротивления равны При параллельном соединении Тогда отношение сопротивлений равно |
Ответ:
если бы две проволоки находились при температуре 20 ºС, то сопротивление данного участка было бы в 1,1 раз больше.