Угловая частота ω
(в радианах в секунду) больше частоты
ν
(в циклах в секунду, также называемая ) в 2
π раз
. На этом рисунке для обозначения частоты используется символ
ν
, а не
f
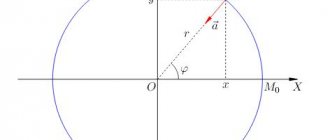
. Сфера, вращающаяся вокруг оси. Точки дальше от оси перемещаются быстрее, удовлетворяя
ω
=
v
/
r
.
В физике , угловая частота
ω
(также упоминаемые условиями
угловой скорости
,
радиальная частота
,
круговая частота
,
орбитальная частота
,
радиан частоты
, и
круговая частота
) является скалярной мерой скорости вращения. Он относится к угловому смещению в единицу времени (например, при вращении) или скорости изменения фазы синусоидальной формы волны (например, в колебаниях и волнах), или как скорость изменения аргумента синусоидального сигнала. функция. Угловая частота (или угловая скорость) — это величина угловой скорости вектора величины . [1]
Один оборот равен 2π радиан , поэтому [1] [2]
ω знак равно 2 π Т знак равно 2 π ж , {\ displaystyle \ omega = {{2 \ pi} \ над T} = {2 \ pi f},}
куда:
ω
— угловая частота или угловая скорость (измеряется в радианах в секунду ),
T
— период (измеряется в секундах ),
f
— обычная частота (измеряется в герцах ) (иногда обозначается
буквой ν
).
Единицы [ править ]
В единицах угловая частота обычно выражается в радианах в секунду , даже если она не выражает значение вращения. С точки зрения анализа размеров , единица Герц (Гц) также верна, но на практике она используется только для обычной частоты f
и почти никогда для
ω
. Это соглашение используется, чтобы помочь избежать путаницы [3], которая возникает при работе с частотой или постоянной Планка, поскольку единицы измерения угла (цикл или радиан) опускаются в СИ. [4] [5] [6] [7] [8]
При цифровой обработке сигналов угловая частота может быть нормализована частотой дискретизации , давая нормированную частоту .
Номинальная скорость вращения
Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:
Т = 1/v.
К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.
Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.
Прибор для измерения частоты вращения – тахометр Testo 477
Примеры [ править ]
Круговое движение [ править ]
Основная статья: Круговое движение
Во вращающемся или орбитальном объекте, существует зависимость между расстоянием от оси, , тангенциальная скорость , и угловая частота вращения. За один период тело, совершая круговое движение, преодолевает расстояние . Это расстояние также равна окружности пути , проходимый телом, . Уравнивая эти две величины и вспоминая связь между периодом и угловой частотой, получаем: р {\ displaystyle r} v {\ displaystyle v} Т {\ displaystyle T} v Т {\ displaystyle vT} 2 π р {\ displaystyle 2 \ pi r} ω знак равно v / р . {\ displaystyle \ omega = v / r.}
Колебания пружины [ править ]
| Часть серии по |
| Классическая механика |
| F знак равно d d т ( м v ) {\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})} Второй закон движения |
|
ветви
|
Основы
|
Составы
|
Основные темы
|
Вращение
|
Ученые
|
| Категории ► Классическая механика |
|
Предмет, прикрепленный к пружине, может колебаться . Если предположить, что пружина идеальная и безмассовая без демпфирования, то движение будет простым и гармоничным с угловой частотой, задаваемой [9]
ω = k m , {\displaystyle \omega ={\sqrt {\frac {k}{m}}},}
куда
k
— жесткость пружины ,
m
— масса объекта.
ω называется собственной частотой (которую иногда можно обозначать как ω 0 ).
Когда объект колеблется, его ускорение можно рассчитать по формуле
a = − ω 2 x , {\displaystyle a=-\omega ^{2}x,}
где x
— смещение из положения равновесия.
Используя «обычную» частоту оборотов в секунду, это уравнение будет
a = − 4 π 2 f 2 x . {\displaystyle a=-4\pi ^{2}f^{2}x.}
LC схемы [ править ]
Резонансная угловая частота в последовательном LC-контуре равна квадратному корню из обратной величины произведения емкости ( C,
измеренной в фарадах ) и индуктивности контура (
L
, в единицах СИ — генри ): [10]
ω = 1 L C . {\displaystyle \omega ={\sqrt {\frac {1}{LC}}}.}
Добавление последовательного сопротивления (например, из-за сопротивления провода в катушке) не изменяет резонансную частоту последовательного LC-контура. Для параллельной настроенной схемы приведенное выше уравнение часто является полезным приближением, но резонансная частота действительно зависит от потерь в параллельных элементах.
Основные формулы и уравнения.
Переменным электрическим током, или просто переменным током, называется электрический ток, изменяющийся с течением времени. Значение тока в рассматриваемый момент времени называется мгновенным значением тока
. В технике обычно применяют периодический электрический ток, мгновенные значения которого повторяются через равные промежутки времени. Наиболее широкое применение получил синусоидальный ток, т.е. ток, являющийся синусоидальной функцией времени.
Мгновенное значение синусоидального тока определяется по формуле
, (1)
где i –
мгновенное значение синусоидального тока,
а
;
Iм
– максимальное значение или амплитуда тока,
а
;
ω –
угловая частота, 1/сек;
φi –
начальная фаза;
t –
время, сек.
Значение аргумента синусоидального тока ωt
+
φi
, отсчитываемое от ближайшей предшествующей точки перехода этого тока через нуль к положительному значению, называется
фазой синусоидального тока
, а величина
φi
, определяющая значение фазы синусоидального тока в начальный момент времени (
t =
0), называется
начальной фазой синусоидального тока
.
Период электрического тока – наименьший промежуток времени, по истечению которого мгновенные значения периодического тока повторяются.
Частота тока есть величина, обратная периоду тока, т.е. число периодов в секунду:
, (2)
где f –
частота тока,
Гц
;
Т –
период тока;
сек
.
Частоту тока можно выразить через число пар полюсов генератора переменного тока и скорость вращения (число оборотов в минуту) его, т.е.
, (3)
где р –
число пар полюсов;
п –
скорость вращения генератора переменного тока,
об/мин.
Угловая частота синусоидального тока равна частоте синусоидального тока, умноженной на 2π, т.е.
, (4)
Действующее значение периодического тока определяется по формуле:
, (5)
где I –
действующее значение периодического тока,
а
.
При синусоидальном токе действующее значение тока
. (6)
Если ток, ЭДС или напряжение изменяются по синусоидальному закону, то его действующее значение составляет 0,707 амплитудного значения:
Среднее значение синусоидального тока за положительную половину
, (7)
где Iср
– среднее значение синусоидального тока,
а
.
Коэффициент формы кривой тока называют отношение действующего значения переменного тока I
к его среднему значению
Iср
:
, (8)
где kср
– коэффициент формы кривой тока.
Для синусоидального тока коэффициент формы кривой равен 1,11.
Типовые задачи с решениями
1. Генератор переменного тока имеет частоту вращения 2800 об/мин. определить частоту, период и угловую частоту электрического тока, если число пар полюсов генератора равно 6.
Решение. Частота электрического тока генератора
Период и угловая скорость
2. Мгновенные значения тока и напряжения потребителя
Определить амплитудные и действующие значения тока и напряжения, их начальные фазы. Построить векторную диаграмму для t
= 0.
Решение. Амплитудные значения Im
= 18 A,
Um
= 210 В; действующие значения
Начальная фаза тока φi
= — 30о, напряжения
φu
= 0. На рисунке 1 представлена векторная диаграмма для
t
= 0.
Рисунок 1.
3. Напряжение, приложенное к неразветвленной цепи переменного тока, ток Определить время и угол сдвига по фазе между ними, их действующие значения, мгновенные значения для t
= 0, если
f
= 20 Гц.
Решение. Угол сдвига по фазе между двумя синусоидально изменяющимися сигналами
Временной сдвиг
Действующие значения
Мгновенные значения тока и напряжения для t
= 0
Векторная диаграмма представлена на рисунке 2.
Рисунок 2.
3. В однородном магнитном поле с индукцией В
= 0,6 Тл с частотой
п
= 1200 об/мин вращается прямоугольная рамка площадью
S =
25 см2. Определить максимальную амплитуду наведенное ЭДС и записать закон изменения ЭДС по времени при условии, что при
t
= 0 рамка параллельна линиям магнитной индукции.
Решение. Частота наведенной в рамке ЭДС
Магнитный поток, пронизываемый рамку,
Мгновенное значение ЭДС, наведенное в рамке,
Тогда амплитудное значение ЭДС при т.е.
5. В двух параллельно включенных приемниках проходят токи Определить амплитудное значение и начальную фазу тока в неразветвленной цепи и записать выражение для мгновенного значения этого тока.
Решение. Задачу можно решить двумя способами: графически и аналитически. Решим ее аналитически. Амплитуда тока
Найдем начальную фазу искомого тока:
Мгновенное значение тока
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Определить период сигнала, если частота переменного тока f
= 400 Гц; 25 кГц; 2 кГц; 40 Гц; 1250 Гц.
2. Переменный синусоидальный сигнал имеет период Т
= 0,2 с; 1,0 с; 40 мс; 50; 250; 0,8 мкс. Определить для этих значений
Т
частоту
f
.
3. Определить угловую частоту синусоидального тока, если период Т
= 2,5·10-4; 10-3; 20·10-2; 5·10-5; 8·10-4; 4·10-6 с.
4. Угловая частота переменного тока ω = 3140; 942; 12560; 5024; 94200; 10048 1/с. Определить частоту и период сигнала.
5. Периода переменного тока, вырабатываемого генератором, Т
= 0,005 с. Частота вращения
п
= 1500 об/мин. Определить число пар полюсов.
6. Два генератора переменного тока работают параллельно на один потребитель, вырабатывая токи одной частоты. Число пар полюсов у первого генератора 3, у второго 4. Определить частоту вращения второго генератора, если у первого п
1 = 800 об/мин.
7. Генератор, имеющий 24 полюса, должен выдавать сигнал с частотой f
= 28 Гц. Определить необходимую частоту вращения ротора, его угловую скорость, а также период и угловую частоту выходного сигнала.
8. Определить число пар полюсов у генератора с частотой вращения п
1 = 900 об/мин, если он работает параллельно со вторым, имеющим пять пар полюсов и частоту вращения
п
2 = 1800 об/мин. Определить частоту сигнала
f = f
1 =
f
2.
9. Определить частоту вращения ротора генератора переменного тока, имеющего восемь пар полюсов, если Т
= 1,48·10-3 с.
10. Действующее значение переменного тока в цепи I
= 10,5 А при частоте
f
= 1200 Гц. Определить его амплитудное значение, период и угловую частоту.
11. Амплитудное значение напряжения переменного тока с периодом Т
= 2,23 мс составляет 220 В. Определить действующее значение этого напряжения и его частоту.
12. Амплитудное значение переменного тока частотой f
= 800 Гц составляет 450 мА. Определить действующее значение тока, угловую частоту и период.
13. Мгновенное значение тока i
= 16 sin 157
t
A. Определить амплитудное и действующее значения этого тока и его период.
14. Амплитудное значение напряжения, приложенного к цепи, Um =
120В, начальная фаза
φu
= π/4. Записать выражение мгновенного значения этого напряжения, определить его действующее значение.
15. Действующее значение переменного тока в цепи I
= 2,9 А, начальная фаза . Записать выражение для мгновенного значения тока в цепи
⇐ Предыдущая4Следующая ⇒
Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)…
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между…
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Ссылки и примечания [ править ]
- ^ ab
Каммингс, Карен; Холлидей, Дэвид (2007).
Понимание физики
. Нью-Дели: John Wiley & Sons Inc., авторизованная перепечатка для Wiley — Индия. стр. 449, 484, 485, 487. ISBN 978-81-265-0882-2 .(UP1) - Holzner, Стивен (2006). Физика для чайников
. Хобокен, Нью-Джерси: Wiley Publishing Inc., стр.201 . ISBN 978-0-7645-5433-9 . угловая частота. - Лернер, Лоуренс С. (1996-01-01). Физика для ученых и инженеров
. п. 145. ISBN 978-0-86720-479-7 . - Мор, JC; Филлипс, WD (2015). «Безразмерные единицы в СИ». Метрология
.
52
(1): 40–47. arXiv : 1409.2794 . Bibcode : 2015Metro..52 … 40M . DOI : 10.1088 / 0026-1394 / 52/1/40 . S2CID 3328342 . - Перейти
↑ Mills, IM (2016). «В единицах радиан и цикл для угла плоскости величины».
Метрология
.
53
(3): 991–997. Bibcode : 2016Metro..53..991M . DOI : 10.1088 / 0026-1394 / 53/3/991 . - «Единицы СИ необходимо реформировать, чтобы избежать путаницы» . От редакции. Природа
.
548
(7666): 135. 7 августа 2011 г. doi : 10.1038 / 548135b . PMID 28796224 . - PR Бункер; IM Mills; Пер Дженсен (2019). «Постоянная Планка и ее единицы». J Quant Spectrosc Radiat Transfer
.
237
: 106594. дои : 10.1016 / j.jqsrt.2019.106594 . - PR Бункер; Пер Дженсен (2020). «Постоянная Планка действия А ». J Quant Spectrosc Radiat Transfer
.
243
: 106835. дои : 10.1016 / j.jqsrt.2020.106835 . h {\displaystyle h} - Serway, Raymond A .; Джуэтт, Джон В. (2006). Основы физики
(4-е изд.). Белмонт, Калифорния: Brooks / Cole — Thomson Learning. стр. 375, 376, 385, 397. ISBN 978-0-534-46479-0 . - Нахви, Махмуд; Эдминистер, Джозеф (2003). Очерк теории и проблем электрических цепей Шаума
. Компании МакГроу-Хилл (McGraw-Hill Professional). стр. 214, 216. ISBN 0-07-139307-2 .(LC1)
Связанное чтение:
- Оленик, Ричард П .; Апостол, Том М .; Гудштейн, Дэвид Л. (2007). Механическая Вселенная
. Нью-Йорк: Издательство Кембриджского университета. С. 383–385, 391–395. ISBN 978-0-521-71592-8 .