The angular frequency ω
(in radians per second) is greater than the frequency
ν
(in cycles per second, also called ) by a
factor of 2 π
.
ν
is used to represent frequency rather than
f
.
A sphere rotating around an axis. Points further from the axis move faster, satisfying ω
=
v
/
r
.
In physics, angular frequency
ω
(also referred to by the terms
angular velocity
,
radial frequency
,
circular frequency
,
orbital frequency
,
radian frequency
, and
circular frequency
) is a scalar measure of rotational speed. It refers to the angular displacement per unit time (such as in rotation) or the rate of change of phase of a sine waveform (such as in oscillations and waves), or as the rate of change of the argument of a sine wave. function. Angular frequency (or angular velocity) is the magnitude of the angular velocity of the quantity vector. [1]
One revolution is equal to 2π radians, so [1] [2]
ω = 2 π T = 2 π f , {\displaystyle \omega ={{2\pi }\over T}={2\pi f},}
where:
ω
is the angular frequency or angular velocity (measured in radians per second),
T
is the period (measured in seconds),
f
is the ordinary frequency (measured in hertz) (sometimes denoted by
the letter ν
).
Units[edit]
In units, angular frequency is usually expressed in radians per second, even if it does not express a rotation value. From a dimensional analysis point of view, the unit Hertz (Hz) is also correct, but in practice it is only used for the usual frequency f
and almost never for
ω
. This convention is used to help avoid confusion [3] that arises when working with frequency or Planck's constant, since the units of angle (cycle or radian) are omitted in SI. [4] [5] [6] [7] [8]
In digital signal processing, the corner frequency can be normalized by the sampling rate, giving the normalized frequency.
Rated rotation speed
Before defining this concept, it is necessary to determine what the nominal operating mode of a device is. This is the order of operation of the device in which the greatest efficiency and reliability of the process are achieved over a long period of time. Based on this, the nominal rotation speed is the number of revolutions per minute when operating in nominal mode. The time required for one revolution is 1/v seconds. It is called the rotation period T. This means that the relationship between the rotation period and frequency has the form:
T = 1/v.
For your information. The rotational speed of the asynchronous motor shaft is 3000 rpm, this is the rated rotation speed of the output shaft shank at the nominal operating mode of the electric motor.
How to find or find out the rotation frequencies of various mechanisms? For this, a device called a tachometer is used.
Device for measuring rotation speed - tachometer Testo 477
Examples[edit]
Circular motion[edit]
Main article: Circular motion
In a rotating or orbital object, there is a relationship between distance from the axis, tangential velocity, and angular frequency. In one period, the body, making a circular motion, covers a distance. This distance is also equal to the circumference of the path traversed by the body, . Equating these two quantities and recalling the relationship between period and angular frequency, we obtain: } ω = v / r . {\displaystyle \omega =v/r.}
Spring vibrations[edit]
| Part of the series on |
| Classical mechanics |
| F = dd t ( m v ) {\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})} Second Law of Motion |
|
branches
|
Basics
|
Compositions
|
Main themes
|
Rotation
|
Scientists
|
| Categories ► Classical mechanics |
|
An object attached to a spring may vibrate. If we assume that the spring is ideal and massless without damping, then the movement will be simple and harmonious with the angular frequency given by [9]
ω = km , {\displaystyle \omega ={\sqrt {\frac {k}{m}}},}
where
k
is the spring stiffness,
m
is the mass of the object.
ω is called the natural frequency (which can sometimes be written as ω 0 ).
When an object vibrates, its acceleration can be calculated using the formula
a = − ω 2 x , {\displaystyle a=-\omega ^{2}x,}
where x
— displacement from the equilibrium position.
Using a "normal" rpm frequency, this equation would be
a = − 4 π 2 f 2 x . {\displaystyle a=-4\pi ^{2}f^{2}x.}
LC circuits[edit]
The resonant angular frequency in a series LC circuit is equal to the square root of the reciprocal of the product of the capacitance ( C,
measured in farads) and loop inductance (
L
, in SI units - Henry): [10]
ω = 1 LC.
{\displaystyle \omega ={\sqrt {\frac {1}{LC}}}.} Adding series resistance (for example, due to wire resistance in a coil) does not change the resonant frequency of the series LC circuit. For a parallel tuned circuit, the above equation is often a useful approximation, but the resonant frequency does depend on the losses in the parallel elements.
Basic formulas and equations.
⇐ PreviousPage 4 of 6Next ⇒Alternating current, or simply alternating current, is an electrical current that changes over time. The current value at the considered moment in time is called the instantaneous current value
. In technology, periodic electric current is usually used, the instantaneous values of which are repeated at regular intervals. The most widely used is sinusoidal current, i.e. current, which is a sinusoidal function of time.
The instantaneous value of the sinusoidal current is determined by the formula
, (1)
where i –
instantaneous value of sinusoidal current,
a
;
Im
– maximum value or current amplitude,
and
;
ω –
angular frequency, 1/sec;
φi –
initial phase;
t –
time, sec.
The value of the sinusoidal current argument ωt
+
φi
, counted from the nearest previous point of transition of this current through zero to a positive value, is called
the phase of the sinusoidal current
, and the value of
φi
, which determines the value of the phase of the sinusoidal current at the initial moment of time (
t =
0), is called
the initial phase of the sinusoidal current
.
The period of electric current is the shortest period of time after which the instantaneous values of the periodic current are repeated.
The frequency of the current is the reciprocal of the period of the current, i.e. number of periods per second:
, (2)
where f –
current frequency,
Hz
;
T -
current period;
sec
.
The frequency of the current can be expressed through the number of pole pairs of the alternator and its rotation speed (rpm), i.e.
, (3)
where p –
number of pole pairs;
P -
rotation speed of the alternator,
rpm.
The angular frequency of the sinusoidal current is equal to the frequency of the sinusoidal current multiplied by 2π, i.e.
, (4)
The effective value of the periodic current is determined by the formula:
, (5)
where I –
effective value of the periodic current,
a
.
For sinusoidal current, the effective current value is
. (6)
If the current, EMF or voltage changes according to a sinusoidal law, then its effective value is 0.707 of the amplitude value:
Average value of sinusoidal current for the positive half
, (7)
where Iav
– average value of sinusoidal current,
a
.
The current waveform coefficient is called the ratio of the effective value of the alternating current I
to its average value
Iav
:
, (8)
where ksr
– current waveform coefficient.
For sinusoidal current, the waveform factor is 1.11.
Typical problems with solutions
1. The alternator has a rotation speed of 2800 rpm. determine the frequency, period and angular frequency of the electric current if the number of generator pole pairs is 6.
Solution. Generator electric current frequency
Period and angular velocity
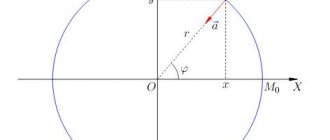
2. Instantaneous values of consumer current and voltage
Determine the amplitude and effective values of current and voltage, their initial phases. Construct a vector diagram for t
= 0.
Solution. Amplitude values Im
= 18 A,
Um
= 210 V; effective values
Initial current phase φi
= - 30°, voltage
φu
= 0. Figure 1 shows a vector diagram for
t
= 0.
Picture 1.
3. Voltage applied to an unbranched AC circuit, current Determine the time and phase shift angle between them, their effective values, instantaneous values for t
= 0 if
f
= 20 Hz.
Solution. Phase angle between two sinusoidally varying signals
Time shifting
Effective values
Instantaneous current and voltage values for t
= 0
The vector diagram is shown in Figure 2.
Figure 2.
3. In a uniform magnetic field with induction B
= 0.6 T with a frequency
n
= 1200 rpm, a rectangular frame with an area
S =
25 cm2 rotates.
Determine the maximum amplitude of the induced emf and write down the law of change of emf over time, provided that at t
= 0 the frame is parallel to the lines of magnetic induction.
Solution. Frequency of the EMF induced in the frame
The magnetic flux passing through the frame
The instantaneous value of the emf induced in the frame is
Then the amplitude value of the EMF at i.e.
5. Currents flow in two parallel-connected receivers. Determine the amplitude value and initial phase of the current in an unbranched circuit and write down the expression for the instantaneous value of this current.
Solution. The problem can be solved in two ways: graphically and analytically. Let's solve it analytically. Current amplitude
Let's find the initial phase of the desired current:
Instantaneous current value
TASKS FOR INDEPENDENT SOLUTION
1. Determine the signal period if the alternating current frequency f
= 400 Hz; 25 kHz; 2 kHz; 40 Hz; 1250 Hz.
2. An alternating sinusoidal signal has a period T
= 0.2 s;
1.0 s; 40 ms; 50; 250; 0.8 µs. Determine
the frequency
f
of T.
3. Determine the angular frequency of the sinusoidal current if the period T
= 2.5·10-4; 10-3; 20·10-2; 5·10-5; 8·10-4; 4·10-6 s.
4. Angular frequency of alternating current ω = 3140; 942; 12560; 5024; 94200; 10048 1/s. Determine the frequency and period of the signal.
5. Period of alternating current generated by the generator, T
= 0.005 s.
Rotation speed n
= 1500 rpm. Determine the number of pole pairs.
6. Two alternating current generators operate in parallel for one consumer, generating currents of the same frequency. The number of pole pairs for the first generator is 3, for the second 4. Determine the rotation frequency of the second generator if the first one has
1 = 800 rpm.
7. A generator having 24 poles must produce a signal with a frequency f
= 28 Hz. Determine the required rotor speed, its angular velocity, as well as the period and angular frequency of the output signal.
8. Determine the number of pole pairs for a generator with a rotation speed n
1 = 900 rpm, if it works in parallel with the second one, which has five pairs of poles and a rotation speed
n
2 = 1800 rpm.
Determine the frequency of the signal f = f
1 =
f
2.
9. Determine the rotor speed of an alternating current generator having eight pairs of poles, if T
= 1.48·10-3 s.
10. Effective value of alternating current in circuit I
= 10.5 A at frequency
f
= 1200 Hz. Determine its amplitude value, period and angular frequency.
11. Amplitude value of alternating current voltage with period T
= 2.23 ms is 220 V. Determine the effective value of this voltage and its frequency.
12. Amplitude value of alternating current with frequency f
= 800 Hz is 450 mA. Determine the effective current value, angular frequency and period.
13. Instantaneous current value i
= 16 sin 157
t
A. Determine the amplitude and effective values of this current and its period.
14. Amplitude value of the voltage applied to the circuit, Um =
120V, initial phase
φu
= π/4. Write down the expression for the instantaneous value of this voltage and determine its effective value.
15. Effective value of alternating current in circuit I
= 2.9 A, initial phase. Write down an expression for the instantaneous value of the current in the circuit
⇐ Previous4Next ⇒
What does the IS operation and maintenance department do? Responsible for the safety of data (copying schedules, copying, etc.)…
WHAT IS CONFIDENT BEHAVIOR IN INTERPERSONAL RELATIONSHIPS? Historically, there are three main patterns of differences that exist between...
System of Protected Areas in the USA The study of specially protected natural areas (SPNA) in the USA is of particular interest for many reasons...
WHAT HAPPENS IN ADULT LIFE? If you are still connected to your mother in the wrong way, you are avoiding separation and independent adult existence...
Didn't find what you were looking for? Use Google search on the site:
Links and notes[edit]
- ^ a b
Cummings, Karen;
Halliday, David (2007). Understanding Physics
. New Delhi: John Wiley & Sons Inc. Authorized reprint for Wiley - India. pp. 449, 484, 485, 487. ISBN 978-81-265-0882-2.(UP1) - Holzner, Stephen (2006). Physics for Dummies
. Hoboken, NJ: Wiley Publishing Inc., p.201. ISBN 978-0-7645-5433-9. angular frequency. - Lerner, Lawrence S. (1996-01-01). Physics for Scientists and Engineers
. paragraph 145. ISBN 978-0-86720-479-7. - Mohr, J.C.; Phillips, W. D. (2015). "Dimensionless units in SI". Metrology
.
52
(1): 40–47. arXiv: 1409.2794. Bibcode: 2015Metro..52…40M. DOI: 10.1088/0026-1394/52/1/40. S2CID 3328342. - Jump up
↑ Mills, I. M. (2016).
"In units of radians and cycle for plane angle quantities." Metrology
.
53
(3):991–997. Bibcode: 2016Metro..53..991M. DOI: 10.1088/0026-1394/53/3/991. - "SI units need to be reformed to avoid confusion". From the editor. Nature
.
548
(7666):135. August 7, 2011. doi:10.1038/548135b. PMID 28796224. - PR Bunker; I.M. Mills; Per Jensen (2019). "Planck's constant and its units." J Quant Spectrosc Radiat Transfer
.
237
: 106594. doi: 10.1016/j.jqsrt.2019.106594. - PR Bunker; Per Jensen (2020). "Plank's Constant Action A." J Quant Spectrosc Radiat Transfer
.
243
: 106835. doi: 10.1016/j.jqsrt.2020.106835. h {\displaystyle h} - Serway, Raymond A.; Jewett, John W. (2006). Fundamentals of Physics
(4th ed.). Belmont, CA: Brooks/Cole - Thomson Learning. pp. 375, 376, 385, 397. ISBN 978-0-534-46479-0. - Nahvi, Mahmoud; Edminister, Joseph (2003). Essay on the theory and problems of electrical circuits by Schaum
. McGraw-Hill Professional. pp. 214, 216. ISBN 0-07-139307-2.(LC1)
Related reading:
- Olenick, Richard P.; Apostle, Tom M.; Goodstein, David L. (2007). Mechanical Universe
. New York: Cambridge University Press. pp. 383–385, 391–395. ISBN 978-0-521-71592-8.