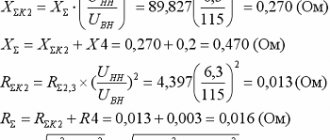Взаимодействия с деталями, отдельными элементами и конструкциями механизма задается с помощью нагрузок. В плоскости задается интенсивность взаимодействия конструкции по длине, а в пространстве – по её площади.
Распределённая нагрузка на балку задается площадью, обозначается буквой q и измеряется в [H/м3] для объемной конструкции, в [H/м2] — для площади, для линейной – в [H/м].
Продемонстрируем это на рисунке:
Нагрузку также можно заменить тягой, рассредоточенной по всей поверхности. Значение определяется по формуле:
Q = q ∗ AB⌈H⌉
здесь AB является тяжестью, q – интенсивностью, которая измеряется в [H/м].
Примечательно, что сила приложена к середине данного отрезка AB.
На данном рисунке представлен расчёт возрастающей нагрузки, которую можно заменить равнодействующей единицей, рассчитываемое по формуле:
Q = qmax ∗ AB/2
где qmax – максимальная интенсивность [Н/м].
Q приложена к точке C, где AC равно: AC = 2/3 AB
Рассматривая функцию q(x), представленную на рисунке:
можно высчитать значение эквивалентной силы по формуле:
Равномерно и неравномерно распределенная нагрузка на балку
Распределение сил, которые лежат в одной плоскости, задается равномерно распределенной тяжестью. Основным обозначением является интенсивность q — предельная тяга, несущая равнодействующую на единицу длины нагруженного участка АВ длиной а.
Единицы измерения распределённой нагрузки [Н/м].
Её также можно заменить на величину Q, которая приложена в середину AB.
Составим формулу: Q = q∗a
Неравномерно распределённую нагрузку чаще всего упрощают, приводя её к эквивалентной равномерно распределенной, чтобы упростить расчеты.
При построении также следует учитывать максимальный прогиб балки, её прочность, расчетную опорную реакцию и моментальную опору.
Распределенная нагрузка
В инженерных расчетах наряду с сосредоточенными силами, которые прилагаются к твердому телу в некоторой точке, встречаются силы, действие которых распределено по определенным участкам объема тела, его поверхности или линии.
Поскольку все аксиомы и теоремы статики формулируются для сосредоточенных сил, то необходимо рассмотреть способы перехода от распределенной нагрузки к сосредоточенным силам.
Рассмотрим некоторые простые случаи распределенной нагрузки тела параллельными силами, которые лежат в одной плоскости вдоль отрезка прямой.
Плоская система распределенных сил характеризуется ее интенсивностью q
, то есть величиной силы, которая приходится на единицу длины нагруженного отрезка. Единицей измерения интенсивности является Ньютон, поделенный на метр (Н/м). Интенсивность может быть постоянной (равномерно распределенная нагрузка) или изменяться по линейным и произвольным законам.
Равномерно распределенная нагрузка (рис. 2.5, а), интенсивность которой q
является постоянной величиной, при статических расчетах заменяется одной сосредоточенной силой, модуль которой
где – длина нагруженного отрезка.
а ) б ) в)
Рисунок 2.5
Эта равнодействующая сила , параллельная силам распределенной нагрузки, направлена в направлении распределенных сил и прикладывается посредине нагруженного отрезка АВ
.
Такая нагрузка имеет место при размещении на теле однородной балки длиной l
с удельным весом
q
.
Распределенная нагрузка с интенсивностью, изменяющейся по линейному закону (рис. 2.5, б), появляется, например, под действием давления воды на дамбу, когда нагружение на дамбу будет наибольшим возле дна водоема и является нулевым возле поверхности воды. При этом величина q
интенсивности растет от нулевого значения к наибольшему значению
qmax
. Равнодействующая
Q
такой нагрузки определяется как вес однородной треугольной пластинки
АВС
, который пропорционален ее площади. Тогда величина этой равнодействующей:
. (55)
Линия действия равнодействующей силы проходит через центр треугольника АВС
на расстоянии от его вершины
А
.
Примером действия сил, распределенных вдоль отрезка прямой по произвольному закону (рис. 2.5, в), является нагрузка плоского перекрытия сугробом снега. Равнодействующая таких сил по аналогии с силой веса численно будет равняться площади фигуры, измеренной в соответствующем масштабе, а линия действия этой равнодействующей будет проходить через центр площади этой фигуры.
Понятие о распределенной нагрузке.
Наряду с рассмотренными выше сосредоточенными силами строительные конструкции и сооружения могут подвергаться воздействию распределенных нагрузок
– по объему, по поверхности или вдоль некоторой линии – и определяемых ее
интенсивностью.
Примером нагрузки, распределенной по площади
, является снеговая нагрузка, давление ветра, жидкости или грунта. Интенсивность такой поверхностной нагрузки имеет размерность давления и измеряется в кН/м2 или килопаскалях (кПа = кН/м2).
При решении задач очень часто встречается нагрузка, распределенная по длине балки
. Интенсивность
q
такой нагрузки измеряется в кН/м.
Рассмотрим балку, загруженную на участке [a
,
b
] распределенной нагрузкой, интенсивность которой изменяется по закону
q
=
q
(
x
). Для определения опорных реакций такой балки нужно заменить распределенную нагрузку эквивалентной сосредоточенной. Это можно сделать по следующему правилу:
Рассмотрим частные случаи распределенной нагрузки.
а) общий случай распределенной нагрузки (рис.24)
Рис.24
q(x) — интенсивность распределенной силы [Н/м],
— элементарная сила.
l
– длина отрезка
Распределенная по отрезку прямой сила интенсивности q(x) эквивалентна сосредоточенной силе
Сосредоточенная сила прикладывается в точке С
(центре параллельных сил) с координатой
б) постоянная интенсивность распределенной нагрузки (рис.25)
Рис. 25
в) интенсивность распределенной нагрузки, меняющаяся по линейному закону (рис.26)
Рис. 26
Расчет составных систем.
Под составными системами будем понимать конструкции, состоящие из нескольких тел, соединенных друг с другом.
Прежде, чем переходить к рассмотрению особенностей расчета таких систем, введем следующее определение.
Статически определимыми называются такие задачи и системы статики, для которых число неизвестных реакций связей не превышает максимально допустимого числа уравнений.
Если число неизвестных больше числа уравнений,
соответствующие
задачи и системы называются статически неопределимыми. При этом разность между числом неизвестных и числом уравнений называется степенью статической неопределимости системы.
Для любой плоской системы сил, действующих на твердое тело, имеется три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных реакций связи.
В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условия равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных реакций связи.
Поясним это на следующих примерах.
1. Пусть центр невесомого идеального блока (пример 4) удерживается при помощи не двух, а трех стержней: АВ
,
ВС
и
BD
и нужно определить реакции стержней, пренебрегая размерами блока.
С учетом условий задачи мы получим систему сходящихся сил, где для определения трех неизвестных: SA
,
SC
и
SD
можно составить по-прежнему систему только двух уравнений: Σ
X
= 0, Σ
Y
=0. Очевидно, поставленная задача и соответствующая ей система будут статически неопределимыми.
2. Балка, жестко защемленная на левом конце и имеющая на правом конце шарнирно-неподвижную опору, загружена произвольной плоской системой сил (рис.27).
Для определения опорных реакций можно составить только три уравнения равновесия, куда войдут 5 неизвестных опорных реакций: XA , YA
,
MA
,
X B
и
YB
. Поставленная задача будет дважды статически неопределимой.
Такую задачу нельзя решить в рамках теоретической механики, предполагая рассматриваемое тело абсолютно твердым.
Рис.27
Вернемся к изучению составных систем, типичным представителем которых является трехшарнирная рама (рис. 28,а
). Она состоит из двух тел:
AC
и
BC
, соединенным
ключевым
шарниром
C
. На примере этой рамы рассмотрим
два способа определения опорных реакций составных систем.
1 способ. Рассмотрим тело AC
, загруженное заданной силой
Р
, отбросив в соответствии с аксиомой 7 все связи и заменив их соответственно реакциями внешних (
XA
,
YA
) и внутренних (
X C
,
YC
) связей (рис. 28,
б
).
Аналогично можно рассмотреть равновесие тела BC
под действием реакций опоры
В
— (
X B
,
YB
) и реакций в соединительном шарнире
C
— (
X C ’
,
YC
’) , где в соответствии с аксиомой 5:
X C
=
X C ’
,
YC
=
YC
’.
Для каждого из этих тел можно составить три уравнения равновесия, таким образом, общее число неизвестных: XA
,
YA
,
X C
=
X C ’
,
YC
=
YC
’,
X B
,
YB
равняется суммарному числу уравнений, и задача является статически определимой.
Напомним, что по условию задачи требовалось определить только 4 опорные реакции, нам же пришлось проделать дополнительную работу, определяя реакции в соединительном шарнире. В этом и заключается недостаток данного способа определения опорных реакций.
2 способ. Рассмотрим равновесие всей рамы АВС
, отбросив только внешние связи и заменив их неизвестными опорными реакциями
XA
,
YA
,
X B
,
YB
.
Полученная система состоит из двух тел и не является абсолютно твердым телом, поскольку расстояние между точками А
и
В
может изменяться вследствие взаимного поворота обеих частей относительно шарнира
С
. Тем не менее можно считать, что совокупность сил, приложенных к раме
АВС
образует систему, если воспользоваться аксиомой отвердевания (рис.28,
в
).
Рис.28
Итак, для тела АВС
можно составить три уравнения равновесия. Например:
ΣMA
= 0;
ΣX
= 0;
ΣY
= 0.
В эти три уравнения войдут 4 неизвестных опорных реакции XA
,
YA
,
X B
и
YB
. Отметим, что попытка использовать в качестве недостающего уравнения, например такое: Σ
M В
= 0 к успеху не приведет, поскольку это уравнение будет линейно зависимым с предыдущими. Для получения линейно независимого четвертого уравнения необходимо рассмотреть равновесие другого тела. В качестве него можно взять одну из частей рамы, например —
ВС
. При этом нужно составить такое уравнение, которое содержало бы «старые» неизвестные
XA
,
YA
,
X B
,
YB
и не содержало новых. Например, уравнение: Σ
X
(
ВС
) = 0 или подробнее: —
XС’
+
X B
= 0 для этих целей не подходит, поскольку содержит «новое» неизвестное
XС
’, а вот уравнение Σ
M С
(
ВС
) = 0 отвечает всем необходимым условиям. Таким образом, искомые опорные реакции можно найти в следующей последовательности:
ΣMA
= 0; →
YB
=
Р
/4;
ΣM В
= 0; →
Y А
= —
Р
/4;
ΣM С
(
ВС
) = 0; →
X B
= —
Р
/4;
ΣX
= 0; →
XА
= -3
Р
/4.
Для проверки можно использовать уравнение: ΣM С
(
АС
) = 0 или, подробнее: —
Y А
∙2 +
XА
∙2 +
Р
∙1 =
Р
/4∙2 -3
Р
/4∙2 +
Р
∙1 =
Р
/2 — 3
Р
/2 +
Р
= 0.
Отметим, что в это уравнение входят все 4 найденные опорные реакции: XА
и
Y А
— в явной форме, а
X B
и
YB
— в неявной, поскольку они были использованы при определении двух первых реакций.
Непрерывно распределенная нагрузка
В механике рассматривают три вида силовых нагрузок:
1) сосредоточенная сила (сила)
– силовая нагрузка, приложенная к телу в определенной точке и изображаемая в виде вектора;
2) пара сил
– система из двух сил, подробно рассмотренная в главе 4;
3) непрерывно распределенная нагрузка
– силовая нагрузка, действие которой распределено вдоль линии, по поверхности или по объему тела.
В данном параграфе рассмотрим последний вид силовых нагрузок. Действие непрерывно распределенной нагрузки на тело характеризуется интенсивностью q
, то есть, величиной силы, приходящейся на единицу длины, поверхности или объема.
Рассмотрим далее только простейший вид такой нагрузки – нагрузку из параллельных сил, непрерывно распределенную вдоль отрезка прямой линии. Действие такой нагрузки на тело принято изображать в виде эпюры
.
Поясним построение эпюры. Вдоль отрезка длиной l
, на котором распределена нагрузка, выберем ось
x
. Вдоль второй оси будем откладывать интенсивность нагрузки
q
. Построим график интенсивности нагрузки на заданном отрезке и между графиком и осью
x
изобразим стрелки, указывающие направление сил нагрузки (см. рис. 82).
Рис. 82
Покажем далее, как такую нагрузку заменить одной равнодействующей силой. Для этого отрезок (0,l
) разобьем на элементарные отрезки длиной
dx
. Действующая на каждый такой отрезок нагрузка может быть приближенно заменена сосредоточенной силой (см. рис. 83), величина которой равна .
Рис. 83
Полученную таким образом систему сосредоточенных параллельных сил можно заменить равнодействующей силой , величина которой после перехода к пределу при найдется по формуле
(77)
Для нахождения точки приложения силы применим теорему Вариньона, согласно которой момент относительно точки О равнодействующей силы равен сумме моментов относительно точки О элементарных сосредоточенных сил . Из этой теоремы после предельного перехода при получим
Отсюда найдем расстояние от начала координат до точки приложения равнодействующей силы
(78)
С помощью формул (77),(78) можно находить равнодействующую силу для непрерывно распределенной нагрузки с произвольной эпюрой. Рассмотрим применение этих формул на примере двух важных для практики простейших случаев.
Пусть на отрезке длиной l
распределена нагрузка с постоянной интенсивностью
q
(см. рис. 84). Вычисляя в этом случае величину равнодействующей и расстояние
h
по формулам (77),(78), получим
(79)
Рис. 84
Таким образом, для равномерно распределенной на отрезке (0,l
) нагрузки равнодействующая сила приложена в середине этого отрезка, равна по величине
ql
и направлена параллельно силам нагрузки.
Рассмотрим теперь нагрузку, у которой интенсивность на отрезке (0,l
) возрастает по линейному закону от нуля до максимального значения (см. рис. 85). В этом случае закон изменения интенсивности запишется в виде
Рис. 85
Величина равнодействующей найдется по формуле (77)
Для расстояния h
из (78) получим
Равновесие системы тел
Пусть в равновесии находится составная конструкция, состоящая из n
твердых тел определенным образом соединенных друг с другом. Для того, чтобы составить полную систему независимых уравнений равновесия такой конструкции, нужно поочередно в качестве объекта равновесия выбрать каждое из тел конструкции, в соответствии с видом действующей системы сил записать для каждого тела независимые уравнения равновесия (см. табл. 1) и после этого все полученные уравнения равновесия объединить в одну общую систему уравнений.
В процессе решения задачи при обозначении на рисунках реакций внутренних связей (сил взаимодействия между телами конструкции) следует учитывать аксиому равенства действия и противодействия.
Обозначим через m
число независимых уравнений равновесия составной конструкции. Пусть в местах соединения тел, входящих в конструкцию, во внешних опорах имеется
k
независимых компонент реакций внутренних и внешних связей. В зависимости от соотношения между
m
и
k
в механике принята следующая классификация конструкций.
Если m=k, то конструкция называется статически определимой.
Для статически определимой конструкции все реакции внешних и внутренних связей можно найти из уравнений статики. Число независимых уравнений совпадает с числом неизвестных реакций.
Если m
Для статически неопределимой конструкции из уравнений статики реакции связей найти не удается, так как число независимых уравнений равновесия меньше числа неизвестных реакций. Для изучения равновесия таких конструкций к уравнениям равновесия статики добавляют
k-m
уравнений совместности деформаций, изучаемых в сопротивлении материалов.
Если m>k, то конструкция называется механизмом с (m-k) степенями свободы.
Равновесие механизма всегда будет шатким (неустойчивым). Для его реализации внешние активные силы не могут быть произвольными, а должны удовлетворять
m-k
условиям, вытекающим из уравнений равновесия.
Приведем примеры, поясняющие введенную классификацию составных конструкций.
Рассмотрим находящуюся в равновесии конструкцию, состоящую из двух стержней АС
и
ВС,
соединенных в точке
С
с помощью шарнира (см. рис. 86). В качестве внешних опор
Рис. 86
выступают жесткая заделка в точке А
и подвижная шарнирная опора в точке
В.
Внешними нагрузками являются сила , приложенная к стержню
АС
и пара сил с моментом
М
, приложенная к стержню
ВС
. В соответствии с изложенной методикой выберем в качестве объектов равновесия поочередно стержни
АС
и
ВС
, обозначив действующие на каждый из них внешние силы, включая реакции связей (см. рис. 87, 88).
Рис. 87
.
Рис. 88
Отметим, что соединительный шарнир в точке С
эквивалентен неподвижному, поэтому его реакцию раскладываем на две составляющих. В соответствии с аксиомой равенства действия и противодействия силы действующие в точке
С
на стержень
АС
со стороны стержня
ВС
(см. рис. 87), и такие же по величине силы действующие на стержень
ВС
со стороны стержня
АС
(см. рис. 88), направлены в противоположные стороны. На каждое из тел конструкции действует произвольная плоская система сил, поэтому общее число независимых уравнений равновесия составной конструкции будет
m=
3+3=6. Независимыми компонентами реакций связей здесь являются их количество
k
=6. Таким образом, в данном случае
m=k
и конструкция, изображенная на рис. 86, является
статически определимой
.
Рассмотрим далее конструкцию, в которой, по сравнению с ранее рассмотренной (см. рис. 86), подвижная шарнирная опора в точке В
заменена неподвижным цилиндрическим шарниром, а остальные элементы конструкции и внешние нагрузки остались неизменными (см. рис. 89).
Рис. 89
Выбрав в качестве объектов равновесия стержни АС
и
ВС
, обозначим действующие на них внешние силы (см. рис. 90, 91). Силы, приложенные к стержню
АС
, остались такими
Рис. 90
Рис. 91
же. Для стержня ВС
изменится реакция в опоре
В
, которую в данном случае следует разложить на две составляющих На каждое из тел конструкции по-прежнему действует произвольная плоская система сил. Общее число независимых уравнений равновесия будет
m=
6. Независимыми компонентами реакций связей в данном случае будут их количество
k=
7. Получили
m, следовательно, конструкция, изображенная на рис. 89, будет статически неопределимой.
Рассмотрим третий вариант составной конструкции, в которой по сравнению с исходной конструкцией, изображенной на рис. 86, жесткая заделка в точке А
заменена неподвижным цилиндрическим шарниром, а остальные элементы конструкции и внешние нагрузки остаются без изменения (см. рис. 92). Считаем, что конструкция находится в равновесии.
Рис. 92
Выбрав в качестве объектов равновесия стержни АС
и
ВС
, обозначим действующие на них внешние силы (см. рис. 93,94). Как и в двух предыдущих случаях на каждое из тел
Рис. 93
Рис. 94
действует плоская произвольная система сил и общее число независимых уравнений равновесия этой конструкции будет m=
6. Независимыми компонентами реакций связей здесь являются их количество
k=
5. Получили
m>k
и
m-k=
1, следовательно, изображенная на рис. 92 конструкция является механизмом с одной степенью свободы.
Глава 7. ТРЕНИЕ И ФЕРМЫ
Трение скольжения
Как отмечалось ранее, если в качестве связи для несвободного тела выступает шероховатая поверхность, то силу реакции удобно раскладывать на две составляющих. Одну из них , перпендикулярную касательной плоскости, проведенной в точке контакта тела с опорной поверхностью, называют нормальной реакцией, а другую , лежащую в касательной плоскости, называют силой трения скольжения
(см
.
рис. 95).
Рис. 95
В теоретической механике рассматривают только сухое трение, когда между соприкасающимися поверхностями нет смазывающего вещества. Но даже в этом случае величина силы трения определяется явлениями механического, электрического, термического, внутримолекулярного характера и детальное изучение трения относится к области физики. Точные формулы здесь очень сложны. В технике обычно используют приближенные законы сухого трения, установленные Ш. Кулоном опытным путем в 1781 г.
1. Сила трения скольжения расположена в общей касательной плоскости, проведенной в точке контакта тела с опорной поверхностью, и направлена в сторону, противоположную направлению скольжения тела (возможного скольжения в случае покоя) под действием активных сил. Величина силы трения в случае покоя зависит от активных сил и может изменяться от нуля до максимального значения, достигаемого в момент выхода тела из положения равновесия:
2. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции)
где безразмерный коэффициент f
называют
коэффициентом трения скольжения.
3.Коэффициент трения скольжения не зависит от площади соприкосновения трущихся поверхностей.
4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей.
Многие задачи на равновесие тела на шероховатой поверхности удобно решать геометрически. Для этой цели введем понятие угла и конуса трения.
Пусть твердое тело под действием активных сил находится на шероховатой поверхности в предельном положении равновесия, когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции (см. рис. 96). В этом случае полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол , который называют углом трения.
Рис. 96
Из рисунка видно, что
то есть, тангенс угла трения равен коэффициенту трения.
Конусом трения
называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Если коэффициент трения во всех направлениях одинаков, то конус трения круговой.
Можно сформулировать условия равновесия тела на шероховатой поверхности, используя конус трения. Если активные силы, действующие на тело, приводятся к равнодействующей силе , то при равновесии тела на шероховатой поверхности равнодействующая активных сил уравновешивается полной реакцией шероховатой поверхности. По аксиоме о равновесии двух сил, приложенных к твердому телу, эти силы равны по величине и направлены в противоположные стороны вдоль одной прямой. Полная реакция проходит через вершину конуса трения, следовательно, через эту вершину проходит и равнодействующая активных сил (см. рис. 86).
При изменении равнодействующей активных сил тело находится в равновесии до тех пор, пока составляющая равнодействующей активных сил, лежащая в общей касательной плоскости соприкасающихся поверхностей, не будет превышать по величине наибольшее значение силы трения . Предельным случаем равновесия тела является случай, когда сила равна по величине силе и равнодействующая активных сил направлена по образующей конуса трения.
Поэтому условие равновесия тела на шероховатой поверхности можно сформулировать в виде: для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину
(см. рис. 97).
Рис. 97
Тело нельзя вывести из равновесия любой по величине активной силой, если ее линия действия проходит внутри конуса трения через его вершину.
Трение качения
При качении цилиндрического катка по опорной плоскости и наличии деформации этих тел соприкосновение катка с плоскостью фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке (см. рис. 98). Если активные силы приложены симметрично относительно среднего сечения катка, то они вызывают одинаковые деформации вдоль всей его образующей и можно изучать только одно среднее сечение катка. Далее будем придерживаться этого предположения и изображать среднее сечение катка в плоскости рисунка.
Рис. 98
Соприкосновение среднего сечения катка с опорной плоскостью происходит по некоторой линии BD. Вдоль этой линии на каток действуют распределенные силы реакции (см. рис. 98). Если эти распределенные силы привести к центру А, то вместо распределенной нагрузки получим главный вектор с составляющими (нормальная реакция) и (сила трения скольжения), а также пару сил с моментом , который называют моментом сопротивления качению
(см. рис. 99).
Рис. 99
Для трения качения установлены приближенные законы аналогично законам трения скольжения.
1. Если каток находится под действием активных сил, стремящихся катить его по опорной поверхности, то возникает пара сил, препятствующая качению, момент которой направлен противоположно угловой скорости катка (в случае покоя катка – противоположно возможной угловой скорости под действием приложенных сил). В случае покоя момент этой пары сил (момент сопротивления качению) зависит от действующих сил и может изменяться от нуля до некоторого максимального значения, достигаемого в момент начала качения катка по опорной поверхности:
2. Наибольший момент сопротивления качению пропорционален нормальному давлению:
Коэффициент пропорциональности δ называется коэффициентом трения качения
и имеет размерность длины.
3. Коэффициент трения качения в довольно широких пределах не зависит от радиуса катка.
4. Коэффициент трения качения зависит от материала и физического состояния поверхностей катка и опорной поверхности.
Эти законы позволяют не рассматривать деформации катка и опорной поверхности, считая их абсолютно твердыми телами, касающимися в одной точке.
Сформулированные выше законы трения скольжения и законы трения качения справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся тел и опорных поверхностей.
Расчет ферм
Фермой
называется геометрически неизменяемая конструкция, состоящая из достаточно легких прямолинейных стержней (весом которых по сравнению с внешними нагрузками можно пренебречь), соединенных между собой с помощью шарниров, которые называются
узлами
фермы. При этом внешние нагрузки приложены только в узлах фермы.
Далее будем рассматривать только плоские фермы. Можно доказать, что плоская ферма будет статически определимой, если выполняется равенство
(80)
где n
– число стержней,
k
– число узлов фермы.
Расчет фермы осуществляется в два этапа.
На первом этапе определяются реакции внешних опор. Для этого в качестве объекта равновесия выбирается вся ферма в целом и составляются соответствующие уравнения равновесия.
На втором этапе определяются усилия в стержнях фермы. Эти усилия действуют со стороны стержней на узлы фермы и направлены вдоль соответствующих стержней в ту или другую сторону в зависимости от физического состояния стержня (он может быть сжат или растянут). Расчет усилий в стержнях может осуществляться тремя способами.
1) Методом вырезания узлов.
Здесь в качестве объектов равновесия поочередно выбираются узлы фермы. При этом каждый раз рекомендуется выбирать такой узел, на который действует не более двух стержней с неизвестными усилиями.
2) Метод сечений (Риттера).
В этом случае мысленно проводят сечение фермы, разделяющее ее на две части. В качестве объекта равновесия выбирают одну из частей фермы. При этом сечение следует проводить так, чтобы оно пересекало не более трех стержней с неизвестными усилиями.
3) Графический метод (построение диаграммы Максвелла-Кремоны).
Этот метод будет подробно пояснен ниже при рассмотрении примера решения задачи.
Пример 9
Задана плоская ферма, изображенная на рис. 100. Внешними нагрузками являются силы и , заданные углы показаны на рисунке. Требуется определить реакции опор и усилия во всех стержнях фермы.
Решение
Рис. 100
Для данной фермы число стержней n
=7 (их номера показаны на рис. 100 арабскими цифрами) и число узлов
k
=5 (их номера показаны на рис. 100 римскими цифрами). Условие (80) выполняется, следовательно, ферма является статически определимой.
Начнем с определения опорных реакций. Выберем в качестве объекта равновесия всю ферму. Действующие на нее внешние нагрузки (силы ) уже показаны на рис. 90. Мысленно отбросим связи, заменив их действие соответствующими реакциями: неподвижный шарнир в точке А заменим двумя составляющими реакции , стержневую опору в точке В заменим реакцией (см. рис. 100). Выберем оси координат и составим уравнения равновесия (для краткости обозначим длину стержня 1 через l
):
Из первого уравнения найдем , из третьего уравнения . Далее из второго уравнения найдем .
Перейдем к определению усилий в стержнях фермы. Вначале вычислим эти усилия аналитически, применяя метод вырезания узлов и метод сечений.
Выберем в качестве объекта равновесия узел (см. рис. 101). На этот узел действует реакция стержневой опоры и два стержня 6 и 7. Здесь и далее будем направлять усилия, действующие со стороны стержней на узел, от узла вдоль соответствующего стержня, считая стержни растянутыми. Тогда стержни, в которых усилия при расчетах получились положительными, будут растянутыми, а стержни с отрицательными усилиями будут сжатыми. Выберем оси координат и составим для полученной плоской сходящейся системы сил два уравнения равновесия:
Рис. 101
Решая эту систему уравнений, найдем .
После этого применим метод сечений, мысленно проведя через стержни 1, 3 и 4 сечение, разрезающее ферму на две части. В качестве объекта равновесия выберем правую часть фермы ( см. рис. 102 ). На этот объект
Рис. 102
действуют заданная сила , реакция стержневой опоры и три стержня 1, 3 и 4. Выберем оси координат и для полученной плоской произвольной системы сил запишем три уравнения равновесия:
Решая эту систему уравнений, найдем
Для нахождения усилия в стержне 5 выберем далее в качестве объекта равновесия узел (см. рис. 103). На этот узел действуют три стержня 4, 5 и 6.
Рис. 103
Обозначим на рисунке соответствующие усилия, выберем оси координат и запишем для нахождения одно уравнение равновесия:
Отсюда найдем
Для нахождения усилия в стержне 2 выберем в качестве объекта равновесия узел III (cм. рис. 104). На этот узел действуют три стержня 2, 3, 4 и заданная сила . Обозначим на рисунке соответствующие силы, выберем
Рис. 104
оси координат и запишем для нахождения одно уравнение равновесия:
Отсюда найдем
На этом расчет фермы закончен. Найдены реакции опор и усилия во всех стержнях фермы.
Далее на примере той же фермы разберем графический метод нахождения усилий в стержнях фермы с помощью диаграммы Максвелла-Кремоны.
Для этого изобразим на отдельном рисунке контур фермы, приложим к нему в соответствующих узлах заданные внешние силы и найденные реакции опор, вынося их за контур фермы. Для опорных реакций указываем их истинное направление с учетом полученных при вычислениях знаков (см. рис. 105)
Рис. 105
После этого ограничим на рисунке внешние области между обозначенными силами. Далее обозначим полученные внешние области большими буквами латинского алфавита A, B, C, D, E. Внутренние области фермы, заключенные между ее стержнями, также обозначим буквами F, K, M. Выберем направление обхода фермы, указав его стрелкой на рисунке (на рис. 105 направление обхода выбрано по часовой стрелке).
Переходим теперь непосредственно к построению диаграммы. На этой диаграмме каждой из областей рисунка 105 будет соответствовать точка, обозначенная такой же малой буквой латинского алфавита. Выбрав масштаб сил, проведем построение диаграммы на рис. 106.
Вначале строим многоугольник внешних сил , обходя внешние области в выбранном направлении. Начнем построение диаграммы с
Рис. 106
точки a
, соответствующей внешней области A. Двигаясь вокруг фермы в выбранном направлении, из области A попадаем в область
B
, пересекая силу . На диаграмме для получения точки
b,
соответствующей области
B
, нужно из точки
a
в направлении силы в выбранном масштабе провести отрезок, равный величине силы . Продолжая обход внешних областей фермы, аналогично строим на диаграмме точки
c,d
и
e
. Отметим, что при правильном нахождении опорных реакций многоугольник внешних сил должен получиться замкнутым, то есть, при проведении на диаграмме из точки
e
отрезка, равного силе , мы должны попасть в точку
a
(начало построения).
После этого строим на диаграмме точки, соответствующие внутренним областям фермы. Начинать построение нужно с такай внутренней области, которая граничит с двумя внешними областями. Такой областью, например, является область M
. Она граничит с областью
C
(границей является стержень 6) и с областью
B
(границей является стержень 7). Для построения соответствующей точки
m
на диаграмме нужно через точку
c
провести линию, параллельную стержню 6, и через точку
b
провести линию, параллельную стержню 7. Точку
m
получим как точку пересечения двух указанных линий. Далее можно строить на диаграмме точку, соответствующую области
K
, граничащую с двумя областями
M
и
B
, уже отображенными на диаграмму. Проводя через точку
m
линию, параллельную стержню 5, и через точку
b
линию, параллельную стержню 4, получим точку
k
, совпадающей с точкой
m
. Для получения на диаграмме точки
f
, соответствующей последней внутренней области
F,
можно провести три прямых линии : через точку
a
параллельно стержню 2, через точку
d
параллельно стержню 1 и через точку
k
параллельно стержню 3. При правильном нахождении опорных реакций и точном построении диаграммы эти линии должны пересекаться в одной точке.
После построения диаграммы усилия, действующие на какой-либо узел со стороны стержней фермы, могут быть найдены графически. Поясним метод на примере узла . Будем обходить этот узел в выбранном направлении обхода ( по часовой стрелке). При таком обходе мы пересекаем стержень 6, переходя из области C
в область
M
(см. рис. 105). Усилие, действующее на этот узел, со стороны стержня 6 будет равно отрезку
cm
на диаграмме (рис. 106). Покажем соответствующий вектор на рис. 105. Он направлен вдоль стержня от узла, следовательно, стержень 1 будет растянутым (усилию следует приписать знак плюс). Измерив отрезок
cm
на диаграмме с помощью масштаба найдем
Обходя этот узел в выбранном направлении далее мы пересекаем стержень 7,
переходя из области M
в область
B
. Поэтому усилие, действующее на этот узел, со стороны стержня 7 будет равно отрезку
mb
на диаграмме. Покажем соответствующий вектор на рис. 105. Он направлен вдоль стержня к узлу, следовательно, стержень 1 будет сжатым (усилию следует приписать знак минус). Измерив отрезок
mb
на диаграмме, с помощью масштаба найдем
Аналогично можно графически определить и показать на рис. 105 усилия в остальных стержнях фермы:
Глава 8. ЦЕНТР ТЯЖЕСТИ
Основные понятия
Рассмотрим систему сил, направленных в одну сторону вдоль параллельных прямых. Такая система сил имеет равнодействующую силу, направленную в ту же сторону, равную по величине сумме модулей этих сил
и приложенную в некоторой точке С.
Центром параллельных сил
называется точка приложения равнодействующей силы для системы параллельных сил, которая не изменяется при повороте всех сил системы вокруг параллельных осей, проходящих через их точки приложения, на одинаковый угол в одном направлении (см. рис. 111).
Рис. 111
Выведем формулы для нахождения координат центра параллельных сил. Пусть имеется система параллельных сил . Радиусы-векторы точек их приложения относительно центра О обозначим . Пусть С – центр этой системы параллельных сил, — радиус-вектор точки С (см. рис. 112).
Рис. 112
Введем единичный вектор , параллельный силам. Тогда
По теореме Вариньона
Подставим сюда выражения сил через единичный вектор
Перенеся все члены последнего равенства в левую сторону и вынося вектор за скобки, получим
Это равенство справедливо при любом направлении параллельных сил, т. е. при любом направлении вектора . Отсюда следует, что
и
(80)
Формула (80) позволяет находить радиус-вектор центра параллельных сил. Проецируя обе части этого векторного равенства на оси координат, получим формулы для вычисления координат центра параллельных сил:
(81)
Если в качестве параллельных сил рассмотреть силы тяжести, приложенные к элементарным частицам тела, то соответствующий им центр параллельных сил называется центром тяжести тела.
На основании формулы (80) выведем формулу для нахождения центра тяжести тела. Разобьем тело на элементарные частицы и обозначим вес частицы с номером k. Тогда для радиуса-вектора центра тяжести получим
(82)
где суммирование производится по всем элементарным частицам тела. Знаменатель представляет собой вес тела
Вес элементарной частицы, имеющей объем можно выразить по формуле
где — удельный вес частицы. Подставляя эти значения в (82) и переходя к пределу при для радиуса-вектора центра тяжести окончательно получим
(83)
Если рассматриваемое тело однородное, то и формула (83) примет вид
где V – объем тела.