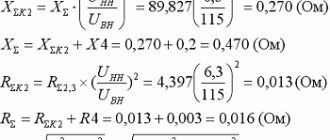Interactions with parts, individual elements and structures of the mechanism are specified using loads. In the plane, the intensity of the interaction of the structure along its length is specified, and in space – along its area.
The distributed load on a beam is specified by the area, denoted by the letter q and measured in [H/m3] for a volumetric structure, in [H/m2] for an area, and in [H/m] for a linear one.
Let's demonstrate this in the figure:
The load can also be replaced by traction distributed over the entire surface. The value is determined by the formula:
Q = q ∗ AB⌈H⌉
here AB is the severity, q is the intensity, which is measured in [H/m].
It is noteworthy that the force is applied to the middle of this segment AB.
This figure shows the calculation of an increasing load, which can be replaced by a resultant unit, calculated using the formula:
Q = qmax ∗ AB/2
where qmax is the maximum intensity [N/m].
Q is applied to point C, where AC is equal to: AC = 2/3 AB
Considering the function q(x) presented in the figure:
you can calculate the value of the equivalent force using the formula:
Uniformly and unevenly distributed load on the beam
The distribution of forces that lie in one plane is determined by a uniformly distributed weight. The main designation is intensity q - the limiting thrust carrying the resultant per unit length of the loaded section AB of length a.
Units for distributed load [N/m].
It can also be replaced by the value Q, which is applied to the middle of AB.
Let's create the formula: Q = q∗a
An unevenly distributed load is most often simplified to an equivalent uniformly distributed load in order to simplify calculations.
When constructing, you should also take into account the maximum deflection of the beam, its strength, the calculated support reaction and instantaneous support.
Distributed load
In engineering calculations, along with concentrated forces that are applied to a solid body at a certain point, there are forces whose action is distributed over certain areas of the volume of the body, its surface or line.
Since all axioms and theorems of statics are formulated for concentrated forces, it is necessary to consider methods of transition from a distributed load to concentrated forces.
Let's consider some simple cases of distributed load of a body by parallel forces that lie in the same plane along a straight line segment.
A flat system of distributed forces is characterized by its intensity q
, that is, the magnitude of the force per unit length of the loaded segment. The unit of intensity is Newton divided by meter (N/m). The intensity can be constant (uniformly distributed load) or vary according to linear and arbitrary laws.
Uniformly distributed load (Fig. 2.5, a), the intensity of which is q
is a constant value, in static calculations it is replaced by one concentrated force, the modulus of which
where is the length of the loaded segment.
a B C)
Figure 2.5
This resultant force, parallel to the forces of the distributed load, is directed in the direction of the distributed forces and is applied in the middle of the loaded segment AB
.
This load occurs when a homogeneous beam of length l
with specific gravity
q
.
A distributed load with an intensity that varies according to a linear law (Fig. 2.5, b) appears, for example, under the influence of water pressure on a dam, when the load on the dam is greatest near the bottom of the reservoir and is zero near the surface of the water. In this case, the value q
intensity increases from zero to the highest value
qmax
.
The resultant Q
of such a load is defined as the weight of a homogeneous triangular plate
ABC
, which is proportional to its area. Then the magnitude of this resultant:
. (55)
The line of action of the resultant force passes through the center of triangle ABC
at a distance from its
top A.
An example of the action of forces distributed along a straight line segment according to an arbitrary law (Fig. 2.5, c) is the load of a flat floor with a snowdrift. The resultant of such forces, by analogy with the weight force, will be numerically equal to the area of the figure measured on the appropriate scale, and the line of action of this resultant will pass through the center of the area of this figure.
The concept of distributed load.
Along with the concentrated forces discussed above, building structures and structures can be exposed to distributed loads
- by volume, along the surface or along a certain line - and determined by its
intensity.
An example of a load distributed over an area
, is the snow load, wind pressure, liquid pressure or soil pressure. The intensity of such a surface load has the dimension of pressure and is measured in kN/m2 or kilopascals (kPa = kN/m2).
When solving problems, a load distributed along the length of a beam
.
The intensity q
of such a load is measured in kN/m.
Let us consider a beam loaded in the section [ a
,
b
] distributed load, the intensity of which varies according to the law
q
=
q
(
x
). To determine the support reactions of such a beam, it is necessary to replace the distributed load with an equivalent concentrated one. This can be done according to the following rule:
Let's consider special cases of distributed load.
a) general case of distributed load (Fig. 24)
Fig.24
q(x) – intensity of distributed force [N/m],
- elemental strength.
l
– length of the segment
The intensity force q(x) distributed along a straight segment is equivalent to a concentrated force
Concentrated force is applied at point C
(center of parallel forces) with coordinate
b) constant intensity of distributed load (Fig. 25)
Rice. 25
c) the intensity of the distributed load, changing according to a linear law (Fig. 26)
Rice. 26
Calculation of composite systems.
By composite systems we mean structures consisting of several bodies connected to each other.
Before moving on to considering the features of the calculation of such systems, we introduce the following definition.
Statically definable are those problems and systems of statics for which the number of unknown constraint reactions does not exceed the maximum allowable number of equations.
If the number of unknowns is greater than the number of equations,
the corresponding
problems and systems are called
statically indeterminate . In this case, the difference between the number of unknowns and the number of equations is called the degree of static indetermination of the system. For any plane system of forces acting on a rigid body, there are three independent equilibrium conditions. Consequently, for any plane system of forces from equilibrium conditions one can find no more than three unknown coupling reactions.
In the case of a spatial system of forces acting on a rigid body, there are six independent equilibrium conditions. Consequently, for any spatial system of forces from equilibrium conditions, no more than six unknown coupling reactions can be found.
Let us explain this with the following examples.
1. Let the center of a weightless ideal block (example 4) be held using not two, but three rods: AB
,
BC
and
BD
and it is necessary to determine the reactions of the rods, neglecting the dimensions of the block.
Taking into account the conditions of the problem, we obtain a system of converging forces, where to determine three unknowns: SA
,
SC
and
SD,
we can still compose a system of only two equations: Σ
X
= 0, Σ
Y
=0. Obviously, the posed problem and the corresponding system will be statically indeterminate.
2. A beam, rigidly clamped at the left end and having a hinged-fixed support at the right end, is loaded with an arbitrary plane system of forces (Fig. 27).
To determine the support reactions, you can create only three equilibrium equations, which will include 5 unknown support reactions: XA, YA
,
MA
,
XB
and
YB
. The stated problem will be twice statically indeterminate.
Such a problem cannot be solved within the framework of theoretical mechanics, assuming the body in question to be absolutely solid.
Fig.27
Let's return to the study of composite systems, a typical representative of which is a three-hinged frame (Fig. 28, a
).
It
consists of two bodies: AC
and
BC
, connected by
key
hinge
C. Using this frame as an example, we will consider two ways to determine the support reactions of composite systems.
1 way. Consider the body AC
, loaded with a given force
P
, discarding all connections in accordance with axiom 7 and replacing them, respectively, with reactions of external (
XA
,
YA
) and internal (
XC
,
YC
) connections (Fig. 28,
b
).
Similarly, we can consider the equilibrium of the body BC
under the influence of support reactions
B
- (
XB
,
YB
) and reactions in the connecting hinge
C
- (
XC '
,
YC
'), where, in accordance with axiom 5:
XC
=
XC '
,
YC
=
YC
'.
For each of these bodies, three equilibrium equations can be drawn up, thus the total number of unknowns: XA
,
YA
,
XC
=
XC '
,
YC
=
YC
',
XB
,
YB
equals the total number of equations, and the problem is statically definable.
Let us recall that according to the conditions of the problem, it was necessary to determine only 4 support reactions, but we had to do additional work by determining the reactions in the connecting hinge. This is the disadvantage of this method of determining support reactions.
Method 2. Consider the equilibrium of the entire frame ABC
, discarding only external connections and replacing them with unknown support reactions
XA
,
YA
,
XB
,
YB
.
The resulting system consists of two bodies and is not an absolutely rigid body, since the distance between points A
and
B
can change due to the mutual rotation of both parts relative to the
hinge
C. Nevertheless, we can assume that the totality of forces applied to the ABC
forms a system, if we use the solidification axiom (Fig. 28,
c
).
Fig.28
So, for the body ABC
three equilibrium equations can be constructed. For example:
ΣMA _
= 0;
Σ X
= 0;
ΣY _
= 0.
These three equations will include 4 unknown support reactions XA
,
YA
,
XB
and
YB
.
Note that an attempt to use, for example, this: Σ M B
= 0 as a missing equation will not lead to success, since this equation will be linearly dependent with the previous ones.
To obtain a linearly independent fourth equation, it is necessary to consider the equilibrium of another body. As it you can take one of the parts of the frame, for example - BC
.
In this case, you need to create an equation that would contain the “old” unknowns XA
,
YA
,
XB
,
YB
and not contain new ones.
For example, the equation: Σ X
(
ВС
) = 0 or in more detail: -
XС'
+
XB
= 0 is not suitable for these purposes, since it contains a “new” unknown
XС
', but the equation Σ
M С
(
ВС
) = 0 meets all the necessary conditions. Thus, the required support reactions can be found in the following sequence:
ΣMA _
= 0;
→ YB
=
P
/4;
Σ M V
= 0;
→ Y A
= -
P
/4;
Σ M C
(
BC
) = 0;
→ XB
= -
Р
/4;
Σ X
= 0;
→ XA
= -3
R
/4.
To check, you can use the equation: Σ M C
(
AC
) = 0 or, in more detail: -
Y A
∙2 +
XA
∙2 +
P
∙1 =
P
/4∙2 -3
P
/4∙2 +
P
∙1 =
P
/2 - 3
P
/2 +
P
= 0.
Note that this equation includes all 4 found support reactions: XA
and
Y A
- in explicit form, and
X B
and
YB
- in implicit form, since they were used in determining the first two reactions.
Continuously distributed load
In mechanics, three types of force loads are considered:
1) concentrated force (force)
– force load applied to the body at a certain point and depicted as a vector;
2) couple of forces
– a system of two forces, discussed in detail in Chapter 4;
3) continuously distributed load
– a force load, the action of which is distributed along a line, over the surface or over the volume of a body.
In this paragraph we will consider the last type of power loads. The action of a continuously distributed load on a body is characterized by intensity q
, that is, the amount of force per unit length, surface or volume.
Let us further consider only the simplest type of such a load - a load of parallel forces continuously distributed along a straight line segment. The effect of such a load on the body is usually depicted in the form of a diagram
.
Let us explain the construction of the diagram. Along a segment of length l
, on which the load is distributed, choose the
x
.
Along the second axis we will plot the load intensity q
.
Let's construct a graph of the load intensity on a given segment and draw arrows between the graph and the x-
indicating the direction of the load forces (see Fig. 82).
Rice. 82
We will show below how to replace such a load with one resultant force. For this purpose, the segment ( 0,l
) will be divided into elementary segments of length
dx
. The load acting on each such segment can be approximately replaced by a concentrated force (see Fig. 83), the magnitude of which is equal to .
Rice. 83
The system of concentrated parallel forces obtained in this way can be replaced by the resultant force, the value of which, after passing to the limit at, can be found by the formula
(77)
To find the point of application of the force, we apply Varignon’s theorem, according to which the moment about the point O of the resultant force is equal to the sum of the moments about the point O of elementary concentrated forces. From this theorem, after passing to the limit at we obtain
From here we find the distance from the origin to the point of application of the resultant force
(78)
Using formulas (77), (78), you can find the resultant force for a continuously distributed load with an arbitrary diagram. Let us consider the application of these formulas using the example of two simple cases that are important for practice.
Let on a segment of length l
the load is distributed with a constant intensity
q
(see Fig. 84).
Calculating in this case the magnitude of the resultant and the distance h
using formulas (77), (78), we obtain
(79)
Rice. 84
Thus, for uniformly distributed on the segment ( 0,l
) load, the resultant force is applied in the middle of this segment, is equal in magnitude
to ql
and is directed parallel to the load forces.
Let us now consider a load whose intensity on the segment ( 0,l
) increases linearly from zero to the maximum value (see Fig. 85). In this case, the law of intensity change will be written in the form
Rice. 85
The magnitude of the resultant can be found using formula (77)
For distance h
from (78) we get
Equilibrium of a system of bodies
Let a composite structure consisting of n
solid bodies connected to each other in a certain way. In order to compose a complete system of independent equilibrium equations for such a structure, it is necessary to select each of the bodies of the structure one by one as an object of equilibrium, in accordance with the type of the operating system of forces, write down independent equilibrium equations for each body (see Table 1) and after that all combine the resulting equilibrium equations into one general system of equations.
In the process of solving the problem, when denoting the reactions of internal connections (interaction forces between structural bodies) in the drawings, one should take into account the axiom of equality of action and reaction.
Let us denote by m
number of independent equilibrium equations of a composite structure.
k
independent components of reactions of internal and external connections
at the points of connection of bodies included in the structure in external supports Depending on the relationship between m
and
k
, the following classification of structures is accepted in mechanics.
If m=k, then the construction is called statically definable.
For a statically definable structure, all reactions of external and internal connections can be found from the static equations. The number of independent equations coincides with the number of unknown reactions.
If m
For a statically indeterminate structure, it is not possible to find the constraint reactions from the static equations, since the number of independent equilibrium equations is less than the number of unknown reactions.
To study the equilibrium of such structures, k-m
equations of compatibility of deformations studied in the strength of materials are added to the static equilibrium equations.
If m>k, then the structure is called a mechanism with (mk) degrees of freedom.
The equilibrium of the mechanism will always be shaky (unstable).
To implement it, external active forces cannot be arbitrary, but must satisfy m-k
conditions arising from the equilibrium equations.
Let us give examples to explain the introduced classification of composite structures.
Let us consider a structure in equilibrium consisting of two rods AC
and
BC
connected at point
C
using a hinge (see Fig. 86). As external supports
Rice. 86
protruding rigid seal at point A
and a movable hinged support at point
B.
External loads are the force applied to the rod
AC
and a pair of forces with a moment
M
applied to the rod
BC
.
AC
and
BC
as objects of equilibrium , designating the external forces acting on each of them, including reaction reactions (see Fig. 87, 88).
Rice. 87
.
Rice. 88
Note that the connecting hinge at point C
is equivalent to a stationary one, so we decompose its reaction into two components.
In accordance with the axiom of equality of action and reaction, the forces acting at point C
on the rod
AC
from the side of the rod
BC
(see Fig. 87), and the same magnitude forces acting on the rod
BC
from the side of the rod
AC
(see Fig. 88), directed in opposite directions.
Each of the bodies of the structure is acted upon by an arbitrary plane system of forces, therefore the total number of independent equilibrium equations of the composite structure will be m=
3+3=6.
The independent components of bond reactions here are their number k
=6.
Thus, in this case m=k
and the design shown in Fig.
86, is statically determinate
.
Let us next consider a structure in which, in comparison with the previously considered (see Fig. 86), a movable hinged support at point B
replaced by a fixed cylindrical hinge, and the remaining structural elements and external loads remained unchanged (see Fig. 89).
Rice. 89
AC as objects of equilibrium
and
BC
, let us denote the external forces acting on them (see Fig. 90, 91).
The forces applied to the rod AC
remained the same
Rice. 90
Rice. 91
same. For rod BC
the reaction in the support
B
, which in this case should be decomposed into two components. Each of the structural bodies is still subject to an arbitrary plane system of forces.
The total number of independent equilibrium equations will be m=
6. The independent components of the coupling reactions in this case will be their number
k=
7. We obtained
m, therefore, the structure shown in Fig.
89, will be statically indeterminate. Let us consider the third version of the composite structure, in which, in comparison with the original structure shown in Fig. 86, hard seal at point A
replaced by a fixed cylindrical hinge, and the remaining structural elements and external loads remain unchanged (see Fig. 92). We assume that the structure is in equilibrium.
Rice. 92
AC as objects of equilibrium
and
BC
, let us denote the external forces acting on them (see Fig. 93,94). As in the two previous cases, for each of the bodies
Rice. 93
Rice. 94
a flat arbitrary system of forces acts and the total number of independent equilibrium equations of this structure will be m=
6. The independent components of the bond reactions here are their number
k =
5. We obtained
m>k
and
m-k =
1, therefore, shown in Fig. 92 design is a mechanism with one degree of freedom.
Chapter 7. FRICTION AND TRUSSES
Sliding friction
As noted earlier, if a rough surface acts as a connection for a non-free body, then it is convenient to decompose the reaction force into two components. One of them, perpendicular to the tangent plane drawn at the point of contact of the body with the supporting surface, is called the normal reaction, and the other, lying in the tangent plane, is called the sliding friction force
(see
Fig
. 95).
Rice. 95
In theoretical mechanics, only dry friction is considered, when there is no lubricant between the contacting surfaces. But even in this case, the magnitude of the friction force is determined by phenomena of a mechanical, electrical, thermal, intramolecular nature, and a detailed study of friction belongs to the field of physics. The exact formulas here are very complex. In technology, approximate laws of dry friction are usually used, experimentally established by C. Coulomb in 1781.
1. The sliding friction force is located in a common tangent plane drawn at the point of contact of the body with the supporting surface, and is directed in the direction opposite to the direction of sliding of the body (possible sliding in the case of rest) under the action of active forces. The magnitude of the friction force in the case of rest depends on the active forces and can vary from zero to the maximum value achieved at the moment the body leaves the equilibrium position:
2. The maximum sliding friction force is proportional to normal pressure (normal reaction)
where the dimensionless coefficient f
called
the sliding friction coefficient.
3. The sliding friction coefficient does not depend on the contact area of the rubbing surfaces.
4. The sliding friction coefficient depends on the material and physical state of the rubbing surfaces.
Many problems involving the balance of a body on a rough surface can be conveniently solved geometrically. For this purpose, we introduce the concept of angle and cone of friction.
Let a solid body, under the action of active forces, be on a rough surface in a limiting equilibrium position when the friction force reaches its greatest value at a given value of the normal reaction (see Fig. 96). In this case, the total reaction of the rough surface is deviated from the normal to the common tangent plane of the rubbing surfaces by the largest angle, which is called the friction angle.
Rice. 96
From the figure it is clear that
that is, the tangent of the friction angle is equal to the friction coefficient.
Friction cone
called a cone described by a complete reaction, built on the maximum frictional force, around the direction of the normal reaction. If the coefficient of friction is the same in all directions, then the cone of friction is circular.
We can formulate the conditions for the equilibrium of a body on a rough surface using a cone of friction. If the active forces acting on a body are reduced to a resultant force, then when the body is in equilibrium on a rough surface, the resultant of the active forces is balanced by the total reaction of the rough surface. According to the axiom about the equilibrium of two forces applied to a solid body, these forces are equal in magnitude and directed in opposite directions along one straight line. The complete reaction passes through the apex of the friction cone; therefore, the resultant of the active forces also passes through this apex (see Fig. 86).
When the resultant of the active forces changes, the body is in equilibrium until the component of the resultant of the active forces, lying in the common tangent plane of the contacting surfaces, does not exceed in magnitude the largest value of the friction force. The limiting case of body equilibrium is the case when the force is equal in magnitude to the force and the resultant of the active forces is directed along the generatrix of the friction cone.
Therefore, the condition for the equilibrium of a body on a rough surface can be formulated in the form: for the equilibrium of a body on a rough surface, it is necessary and sufficient that the line of action of the resultant active forces acting on the body pass inside the friction cone or along its generatrix through its vertex
(see Fig. 97).
Rice. 97
A body cannot be thrown out of balance by any active force of any magnitude if its line of action passes inside the friction cone through its apex.
Rolling friction
When a cylindrical roller rolls along a supporting plane and there is deformation of these bodies, the contact of the roller with the plane actually occurs not along one generatrix, as in the case of absolutely rigid bodies, but along a certain area (see Fig. 98). If active forces are applied symmetrically relative to the middle section of the roller, then they cause equal deformations along its entire generatrix and only one middle section of the roller can be studied. Further we will adhere to this assumption and depict the average section of the skating rink in the plane of the drawing.
Rice. 98
The contact of the middle section of the roller with the supporting plane occurs along a certain line BD. Along this line, distributed reaction forces act on the roller (see Fig. 98). If these distributed forces are brought to the center A, then instead of a distributed load we get a main vector with components (normal reaction) and (sliding friction force), as well as a pair of forces with a moment, which is called the moment of rolling resistance
(see Fig. 99).
Rice. 99
For rolling friction, approximate laws are established similar to the laws of sliding friction.
1. If the roller is under the influence of active forces tending to roll it along the supporting surface, then a pair of forces arises that prevents rolling, the moment of which is directed opposite to the angular velocity of the roller (in the case of the roller at rest, opposite to the possible angular velocity under the influence of the applied forces). In the case of rest, the moment of this pair of forces (moment of rolling resistance) depends on the acting forces and can vary from zero to a certain maximum value achieved at the moment the roller begins to roll on the supporting surface:
2. The highest moment of rolling resistance is proportional to normal pressure:
The proportionality coefficient δ is called the rolling friction coefficient
and has the dimension of length.
3. The rolling friction coefficient, within a fairly wide range, does not depend on the radius of the roller.
4. The rolling friction coefficient depends on the material and physical condition of the surfaces of the roller and the supporting surface.
These laws make it possible not to consider the deformations of the skating rink and the supporting surface, considering them to be absolutely rigid bodies touching at one point.
The laws of sliding friction and the laws of rolling friction formulated above are valid for not very high normal pressures and not too easily deformed bodies and supporting surfaces.
Truss calculation
Fermoy
is a geometrically unchangeable structure consisting of fairly light rectilinear rods (the weight of which can be neglected in comparison with external loads), connected to each other using hinges, which are called
nodes
. In this case, external loads are applied only at the nodes of the truss.
In what follows we will consider only flat trusses. It can be proven that a plane truss will be statically definable if the equality
(80)
where n
– number of rods,
k
– number of truss nodes.
The farm calculation is carried out in two stages.
At the first stage, the reactions of external supports are determined. To do this, the entire truss is selected as an equilibrium object and the corresponding equilibrium equations are drawn up.
At the second stage, the forces in the truss rods are determined. These forces act from the side of the rods on the nodes of the truss and are directed along the corresponding rods in one direction or another, depending on the physical state of the rod (it can be compressed or stretched). The forces in rods can be calculated in three ways.
1) By cutting out knots.
Here, the truss nodes are alternately selected as equilibrium objects. In this case, each time it is recommended to choose a node that is subject to no more than two rods with unknown forces.
2) Method of sections (Ritter).
In this case, a cross section of the truss is mentally drawn, dividing it into two parts. One of the parts of the truss is chosen as the object of equilibrium. In this case, the section should be carried out so that it intersects no more than three rods with unknown forces.
3) Graphical method (constructing a Maxwell-Cremona diagram).
This method will be explained in detail below when considering an example solution to the problem.
Example 9
A flat truss is given, shown in Fig. 100. External loads are forces and , given angles are shown in the figure. It is required to determine the support reactions and forces in all truss rods.
Solution
Rice. 100
For a given truss, the number of rods is n
=7 (their numbers are shown in Fig. 100 in Arabic numerals) and the number of nodes
k
=5 (their numbers are shown in Fig. 100 in Roman numerals). Condition (80) is satisfied, therefore, the truss is statically determinate.
Let's start by defining support reactions. Let us choose the entire farm as the object of equilibrium. The external loads (forces) acting on it are already shown in Fig. 90. Let's mentally discard the connections, replacing their action with the corresponding reactions: replace the fixed hinge at point A with two components of the reaction, replace the rod support at point B with a reaction (see Fig. 100). Let's choose the coordinate axes and draw up equilibrium equations (for brevity, let's denote the length of rod 1 by l
):
From the first equation we find , from the third equation . Next, we find from the second equation.
Let's move on to determining the forces in the truss rods. First, we calculate these forces analytically, using the method of cutting nodes and the method of sections.
Let us choose a node as the object of equilibrium (see Fig. 101). This node is affected by the reaction of the rod support and two rods 6 and 7. Here and further we will direct the forces acting from the rods on the node from the node along the corresponding rod, considering the rods to be stretched. Then the rods in which the forces in the calculations turned out to be positive will be stretched, and the rods with negative forces will be compressed. Let us choose the coordinate axes and compose two equilibrium equations for the resulting flat converging system of forces:
Rice. 101
Solving this system of equations, we find .
After this, we apply the section method, mentally drawing a section through rods 1, 3 and 4, cutting the truss into two parts. Let us choose the right side of the truss as the object of equilibrium (see Fig. 102). To this object
Rice. 102
the given force, reaction of the rod support and three rods 1, 3 and 4 act. Let us choose the coordinate axes and for the resulting flat arbitrary system of forces we write three equilibrium equations:
Solving this system of equations, we find
To find the force in rod 5, we next select a node as an object of equilibrium (see Fig. 103). This unit is acted upon by three rods 4, 5 and 6.
Rice. 103
Let us designate the corresponding forces in the figure, select the coordinate axes and write one equilibrium equation to find:
From here we will find
To find the force in rod 2, we select node III as the object of equilibrium (see Fig. 104). This node is acted upon by three rods 2, 3, 4 and a given force. Let us designate the corresponding forces in the figure and choose
Rice. 104
coordinate axes and write down one equilibrium equation to find:
From here we will find
This completes the farm calculation. The support reactions and forces in all truss rods were found.
Next, using the same truss as an example, we will analyze a graphical method for finding the forces in the truss rods using the Maxwell-Cremona diagram .
To do this, we will depict the contour of the truss in a separate figure, apply the specified external forces and the found reactions of the supports to it at the corresponding nodes, moving them beyond the contour of the truss. For support reactions, we indicate their true direction, taking into account the signs obtained during calculations (see Fig. 105)
Rice. 105
After this, we will limit the external areas between the indicated forces in the figure. Next, we denote the resulting external areas by capital letters of the Latin alphabet A, B, C, D, E. The internal areas of the truss, enclosed between its rods, will also be denoted by the letters F, K, M. We select the direction of bypassing the truss, indicating it with an arrow in the figure (in Fig. 105 the bypass direction is selected clockwise).
We now proceed directly to constructing the diagram. On this diagram, each of the areas of Figure 105 will correspond to a point designated by the same small letter of the Latin alphabet. Having chosen the scale of forces, we will construct the diagram in Fig. 106.
First, we build a polygon of external forces, bypassing the external areas in the chosen direction. Let's start building the diagram with
Rice. 106
points a
, corresponding to the outer area A. Moving around the farm in the chosen direction, from area A we get to area
B
, crossing the force.
On the diagram, to obtain point b,
corresponding to area
B
, you need to draw a segment from point
a
in the direction of the force on the selected scale equal to the magnitude of the force.
Continuing to walk around the outer areas of the farm, we similarly build points c, d
and
e
.
Note that if the support reactions are correctly found, the polygon of external forces should turn out to be closed, that is, when drawing a segment on the diagram from point e
equal to the force , we should get to point
a
(the beginning of construction).
After this, we plot points on the diagram corresponding to the internal areas of the farm. You need to start building from such an internal area that borders two external areas. Such a region, for example, is the region M
.
It borders area C
(the boundary is rod 6) and area
B
(the boundary is rod 7).
To construct the corresponding point m
on the diagram, you need
to draw a line parallel to rod 6
c b
draw a line parallel to rod 7. Point
m
is obtained as the point of intersection of the two indicated lines.
Next, you can build a point on the diagram corresponding to the area K
, bordering on two areas
M
and
B
, already displayed on the diagram.
Drawing a line parallel to rod 5 through point m
and
a line parallel to rod 4 through point
b k
coinciding with point
m
.
f
on the diagram corresponding to the last internal region
F,
three straight lines can be drawn: through point
a
parallel to rod 2, through point
d
parallel to rod 1 and through point
k
parallel to rod 3. If the support reactions are correctly found and the diagram is accurately constructed, these the lines must intersect at one point.
After constructing the diagram, the forces acting on any node from the side of the truss rods can be found graphically. Let's explain the method using the example of a node. We will bypass this node in the selected traversal direction (clockwise). With this bypass we cross rod 6, moving from area C
to area
M
(see Fig. 105).
The force acting on this node from the side of rod 6 will be equal to the segment cm
on the diagram (Fig. 106).
We show the corresponding vector in Fig. 105. It is directed along the rod from the node, therefore, rod 1 will be stretched (the force should be assigned a plus sign). By measuring the segment cm
on the diagram using a scale, we find
Bypassing this node in the chosen direction, we then cross rod 7,
moving from area M
to
area
B. Therefore, the force acting on this node from the side of rod 7 will be equal to the segment mb
in the diagram.
We show the corresponding vector in Fig. 105. It is directed along the rod towards the node, therefore, rod 1 will be compressed (the force should be assigned a minus sign). Having measured the segment mb
on the diagram, using the scale we find
Similarly, it can be graphically determined and shown in Fig. 105 forces in the remaining rods of the truss:
Chapter 8. CENTER OF GRAVITY
Basic Concepts
Let's consider a system of forces directed in one direction along parallel lines. Such a system of forces has a resultant force directed in the same direction, equal in magnitude to the sum of the modules of these forces
and applied at some point C.
Center of parallel forces
is called the point of application of the resultant force for a system of parallel forces, which does not change when all forces of the system are rotated around parallel axes passing through their points of application by the same angle in one direction (see Fig. 111).
Rice. 111
Let us derive formulas for finding the coordinates of the center of parallel forces. Let there be a system of parallel forces. We denote the radius vectors of the points of their application relative to the center O. Let C be the center of this system of parallel forces, be the radius vector of point C (see Fig. 112).
Rice. 112
Let us introduce a unit vector parallel to the forces. Then
According to Varignon's theorem
Let us substitute here the expressions of forces through the unit vector
Moving all the terms of the last equality to the left and taking the vector out of brackets, we get
This equality is valid for any direction of parallel forces, i.e. for any direction of the vector. It follows that
And
(80)
Formula (80) allows you to find the radius vector of the center of parallel forces. Projecting both sides of this vector equality onto the coordinate axes, we obtain formulas for calculating the coordinates of the center of parallel forces:
(81)
If we consider the gravitational forces applied to the elementary particles of a body as parallel forces, then the corresponding center of parallel forces is called the center of gravity of the body.
Based on formula (80), we derive a formula for finding the center of gravity of a body. Let's divide the body into elementary particles and denote the weight of the particle with number k. Then for the radius vector of the center of gravity we obtain
(82)
where the summation is performed over all elementary particles of the body. The denominator is body weight
The weight of an elementary particle with volume can be expressed by the formula
where is the specific gravity of the particle. Substituting these values into (82) and passing to the limit at for the radius vector of the center of gravity we finally obtain
(83)
If the body under consideration is homogeneous, then formula (83) will take the form
where V is the volume of the body.