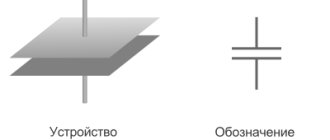
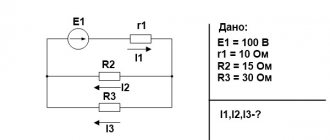
6.4. Сопротивление в цепи синусоидального тока
Если напряжение подключить к сопротивлению R, то через него протекает ток
(6.7)
Анализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе. Формула (6.7) в комплексной форме записи имеет вид
(6.8)
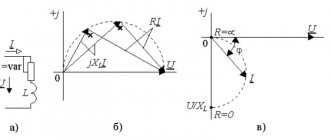
где и — комплексные амплитуды тока и напряжения. Комплексному уравнению (6.8) соответствует векторная диаграмма (рис. 6.4).
Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению. Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току — активным сопротивлением. Рис.6.4 Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.
Синусоидальный ток в электрической цепи с емкостным сопротивлением
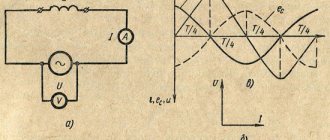
Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение (см. рис. 1), то ток i
через него будет равен
Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u
и
i ,
то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е.
на резисторе напряжение и ток совпадают по фазе.
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
— разделим первый из них на второй:
Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.
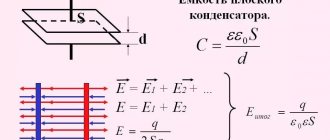
2. Конденсатор
Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение (см. рис. 4), то ток i
через него будет равен
Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на
/2.
Таким образом, если на входы двухлучевого осциллографа подать сигналы
u
и
i
, то на его экране будет иметь место картинка, соответствующая рис. 5.
Введенный параметр называют реактивным емкостным сопротивлением конденсатора
. Как и резистивное сопротивление, имеет размерность
Ом
. Однако в отличие от
R
данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при конденсатор представляет разрыв для тока, а при .
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
— разделим первый из них на второй:
В последнем соотношении — комплексное сопротивление конденсатора. Умножение на соответствует повороту вектора на угол по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.
3. Катушка индуктивности
Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис.  определяется выражением . Тогда для напряжения на зажимах катушки индуктивности можно записать
определяется выражением . Тогда для напряжения на зажимах катушки индуктивности можно записать
Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на
/2
. Таким образом, если на входы двухлучевого осциллографа подать сигналы
u
и
i
, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.
6.5. Индуктивная катушка в цепи синусоидального тока
Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции
(6.9)
Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = eL = 0.
(6.10)
Таким образом, ток в индуктивности отстает по фазе от напряжения на 90o из-за явления самоиндукции. Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:
(6.11)
Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0oo), величина которого зависит от соотношения R и L. Выражение (6.11) в комплексной форме записи имеет вид:
(6.12)
где ZL — полное комплексное сопротивление индуктивной катушки ; ZL — модуль комплексного сопротивления; — начальная фаза комплексного сопротивления; — индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле). Полное сопротивление индуктивной катушки или модуль комплексного сопротивления
.
Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).
Рис. 6.5
Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90o. В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически. Если мы поделим стороны треугольника напряжений на величину тока Im, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).
Из треугольника сопротивлений получим несколько формул: ; ; Рис. 6.6
;
; .
Синусоидальный ток в емкости
Сложение двух функций в тригонометрической форме трудоемко, но легко производится в векторной форме. Векторные диаграммы сложения двух напряжений
В расчетах применяют три формы записи комплексных величин:
1) алгебраическая 2) тригонометрическая 3) показательная, учитывая
Символ j перед мнимой частью комплексного числа в алгебраической форме означает, что мнимая часть повернута по отношению к вещественной на угол 90° в положительном направлении (против часовой стрелки). Переходы из одной формы записи в другие:
где
где
Представленная ранее система дифференциальных уравнений для цепи переменного тока с R, L, С в комплексном виде записывается следующим образом:
Используя выражения , запишем выражение для полного напряжения цепи:
где — комплексное сопротивление; — комплексная амплитуда напряжения; — комплексная амплитуда тока. При замене амплитудных значений на действующие получим закон Ома в комплексной форме:
Величину Z называют полным сопротивлением цепи переменного тока. Первый закон Кирхгофа в комплексной форме:
Второй закон Кирхгофа в комплексной форме:
Векторная диаграмма напряжений для цепи с последовательным соединением R, L, C будет представлять собой прямоугольный треугольник. Треугольник напряжений
Треугольники токов, сопротивлений и мощностей строятся аналогично
Полная мощность S = UI; активная мощность реактивная мощность где
В треугольниках напряжений, токов, сопротивлений и мощностей угол сохраняет свое значение. При параллельном соединении ветвей их проводимости складываются в комплексной форме: Общий ток, согласно первому закону Кирхгофа:
37.
Рис. 2.19
При рассмотрении цепей синусоидального тока до сих пор учитывалось только явление самоиндукции катушек, обусловленное током в цепи. Цепи, в которых наводятся ЭДС между двумя (и более) взаимно связанными катушками, называются индуктивно связанными цепями. Рассмотрим явление возникновения ЭДС в одном из контуров при изменении тока в другом.
Контуры (рис. 2.19) представляют собой плоские тонкие катушки с числами витков и . Поток самоиндукции , созданный током , может быть представлен в виде потока рассеяния , пронизывающего только первый контур, и потока , пронизывающего второй контур
= + .
Аналогично определяем поток самоиндукции второго контура
= + .
Потоки и называют потоками взаимной индукции. Их принято обозначать двумя индексами: первый индекс указывает, с каким контуром сцепляется поток, второй – номер тока, вызвавшего данный поток. Например, поток вызван током , сцепляется с первым контуром. Если направление потока взаимной индукции совпадает с направлением потока самоиндукции данного контура, то говорят, что магнитные потоки и токи контуров направлены согласно. В случае противоположного направления говорят о встречном направлении потоков. Суммарные потоки, пронизывающие первый и второй контуры
= ± ; = ± ,
где «+» соответствует согласному направлению потоков, «–» – встречному направлению.
Полные потокосцепления первого и второго контуров
(2.48)
(2.49)
Отношение потокосцепления взаимной индукции в одной цепи к току в другой называется взаимной индуктивностью
Для линейных электрических цепей всегда выполняется равенство
.
Взаимная индуктивность двух катушек зависит от числа витков, геометрических размеров магнитопровода и взаимного расположения катушек, а также от абсолютной магнитной проницаемости среды (материала магнитопровода). Индуктивную связь двух катушек характеризуют коэффициентом связи
.
Этот коэффициент всегда меньше единицы, так как магнитный поток взаимной индукции всегда меньше потока самоиндукции и может быть увеличен за счет уменьшения потоков рассеяния бифилярной намоткой катушек (двойным проводом) или применением для магнитопровода материала с высокой абсолютной магнитной проницаемостью.
ЭДС взаимной индукции
ЭДС, индуктируемые в первом и втором контурах, с учетом (2.48, 2.49) можно записать в виде
Таким образом, ЭДС каждой катушки определяется алгебраической суммой ЭДС самоиндукции и взаимной индукции. Для определения знака ЭДС взаимной индукции размечают зажимы индуктивно связанных элементов цепи. Два зажима называют одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции и взаимной индукции складываются. Такие выводы обозначают на схемах одинаковыми условными значками, например, точками или звездочками (рис. 2.20 а, б). Одинаково направленные токи и (рис. 2.20 а) относительно зажимов и вызывают совпадающие по направлению потоки самоиндукции ( ) и взаимной индукции ( ). Следовательно, зажимы и являются одноименными. Одноименной является и другая пара зажимов и , но условными значками обозначают только одну пару одноименных выводов, например, и (рис. 2.20 а). Если токи и направлены неодинаково относительно одноименных зажимов (рис. 2.20 б), то имеет место встречное направление потоков самоиндукции и взаимоиндукции.
На схемах магнитопроводы, как правило, не показывают и ограничиваются только обозначением одноименных зажимов (рис. 2.20 в, г).
Одноименные зажимы можно определить опытным путем. Для этого одну из катушек включают в цепь источника постоянного тока, а к другой присоединяют вольтметр постоянного тока. Если в момент подключения источника стрелка измерительного прибора отклоняется, то зажимы индуктивно связанных
Рис. 2.20
катушек, подключенные к положительному полюсу источника и положительному зажиму измерительного прибора, являются одноименными.
Определим знаки ЭДС и напряжения взаимной индукции. Допустим, первая катушка (рис. 2.20 а) разомкнута, а во второй протекает ток . Выберем положительные направления для одинаковыми относительно одноименных зажимов. ЭДС и напряжение взаимной индукции равны, но противоположны по знаку. Действительно, когда 0, потенциал зажима b больше потенциала зажима а, следовательно, 0.
По правилу Ленца знаки и всегда противоположны, поэтому
.
В комплексной форме уравннеие имеет вид
(2.50)
При встречном включении катушек (рис. 2.20 б)
. (2.51)
Из (2.50) и (2.51) видно, что вектор напряжения на взаимной индуктивности сдвинут по фазе относительно вектора тока на угол ±90°.
Сопротивление называется сопротивлением взаимной индуктивности, а – комплексным сопротивлением взаимной индуктивности.
Таким образом, при согласном направлении токов падение напряжения на взаимной индуктивности имеет знак «плюс», при встречном – знак «минус».
38.
Трехфазная система электрических цепей представляет собой совокупность электрических цепей, в которых действуют три синусоидальные Э.Д.С. одной и той же частоты, сдвинутые друг относительно друга по фазе и создаваемые общим источником питания.
Если все три Э.Д.С. равны по значению и сдвинуты по фазе на 1200 по отношению друг к другу, то такая система Э.Д.С. называется симметричной.
Часть трехфазной системы электрических цепей, в которой может протекать один из токов трехфазной системы, называется фазой. Фазой является обмотка генератора, в которой индуцируется Э.Д.С. и приемник, присоединенный к этой обмотке.
Трехфазная система Э.Д.С. создается трехфазными генераторами. В неподвижной части генератора (статоре) размещают три обмотки, сдвинутые в пространстве на 1200. Это фазные обмотки, или фазы, которые обозначают А,В,С, концы обмоток обозначают X,Y,Z. На вращающейся части генератора (роторе) располагают обмотку возбуждения, которая питается от источника постоянного тока. Так обмотки возбуждения создают магнитный поток Фо, постоянный (неподвижный) относительно ротора, но вращающийся вместе с частотой n. Вращение ротора осуществляется каким-либо двигателем.
При вращении ротора, вращающийся вместе с ним магнитный поток пересекает проводники обмотки статора (А-X, B-Y, C-Z) и индуцирует в них синусоидальные Э.Д.С. LA= Em sin Wt LB= Em sin (Wt — [pic]) LC= Em sin (Wt + [pic])
39.
Соединение приемников электрической энергии в «звезду».
При использовании трехфазных систем питания трехфазных потребителей электроэнергии соединение фаз источника и потребителя выполняется обычно по схеме «звезда» или «треугольник».
При соединении фаз трехфазного источника питания или потребителя энергии «звездой» концы фаз источника X, Y, Z или приемника x, y, z объединены в общую нейтральную точку N, а начала фаз подключаются к соответствующим линейным проводам.
Напряжения Ua, Ub, Uc, действующие между началами и концами фаз, являются его фазными напряжениями. Напряжения Uab, Ubc, Uca, действующие между началами фаз потребителя, являются линейными напряжениями.
При соединении в звезду справедливо равенство линейных и фазных токов, m. In = If ; IA = Ia ; IC = Ic .
Для симметричной трехфазной цепи и для трехфазной четырехпроводной цепи. Номинальное (линейное) напряжение в [pic] раз больше фазного.
[pic], т.е. [pic]; [pic]; [pic].
Токи в фазах определяют по закону Ома для цепей переменного тока:
[pic]; [pic]; [pic]; [pic]
Активная Р, реактивная Q и полная мощности потребителя электрической энергии определяют как сумму соответствующих фазных мощностей
P = Pa + Pb + Pc Pф=Iф2 Rф, Qф2=Iф2 X2, Qфс= -Iф2
Xc
Q=Qa+Qв+Qc Qф=QL+Qc
[pic]
В трехфазной четырехпроводной цепи ток в нейтральном проводе определяется на основании первого закона Кирхгофа IN= Ia + Ib + Ic, как векторная сумма фазных токов. При несимметричной нагрузке обрыв нулевого провода (ZN=() вызывает значительное изменение токов и фазных напряжений, что в большинстве случаев недостижимо. Поэтому в нулевой провод предохранители не устанавливают.
При наличии нулевого провода фазные напряжения будут одинаковы UA = UB
= UC.
3. Соединение приемников электрической энергии в «треугольник».
Соединение, при котором начало одной фазы потребителя электроэнергии (или источника питания) соединяется с концами другой его фазы, начало которой соединено с концом третьей фазы, а начало третьей фазы – с концом первой фазы (при этом начала всех фаз подключаются к соответствующим линейным проводам), называется треугольником. При соединении «треугольником» фазные напряжения оказываются равными линейным
Uф = Uл. При симметричной системе питания Uab=Ubc=Uca=UAB=UBC=UCA=Uф=Uл.
При симметричной нагрузке линейные токи в [pic] раз больше фазных: Iл =
[pic].
При несимметричной нагрузке линейные токи равны векторной разности фазных токов соединенных с данным линейным проводом: IA = Iab – Ica ; IB = Ibc – Iab ; IC = Ica – Ibc.
Методические указания к решению задач 1 и2.
Решение задач этой группы требует знания учебного материала «Трехфазные электрические цепи». Е.С. Попов Теоретическая электротехника, 12.1 – 12.12. А.Г. Морозов. Электротехника, электроника и техника 4.1 — 4.5.
Иметь представление об особенностях соединения источников и потребителей в «звезду» и «треугольник», соотношения между линейными и фазными токами и напряжениями, а также умения рассчитывать нагрузку фазы и строить векторные диаграммы при симметричной и несимметричной нагрузках.
40.
⇐ Предыдущая3Следующая ⇒
Рекомендуемые страницы:
6.6. Емкость в цепи синусоидального тока
Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток
;
. (6.13)
Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90o.
Выражение (6.13) в комплексной форме записи имеет вид:
, (6.14)
где — емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.
Если комплексное сопротивление индуктивности положительно , то комплексное сопротивление емкости отрицательно .
На рис. 6.7 изображена векторная диаграмма цепи с емкостью. Вектор тока опережает вектор напряжения на 90o.
Рис. 6.7
Цепь синусоидального тока с емкостным сопротивлением
| Пусть (полагаем ) Ток через емкость пропорционален скорости изменения заряда. |
Графики и имеет вид:
| Для емкостной цепи кривая тока опережает кривую напряжения на четверть периода . |
Таким образом, если , то
Закон Ома в комплексной форме для емкостного элемента имеет вид:
Величина называется комплексным емкостным сопротивлением.
Активная мощность емкостной цепи так же, как и для индуктивной равна нулю, а реактивная мощность определяется выражением:
Векторная диаграмма цепи имеет вид:
Рассмотрим цепь с последовательным соединением и (рис.14).На зажимы А и Д подано синусоидальное напряжение.
| Рис.14 | Согласно 2-му закону Кирхгофа в комплексной форме справедливо уравнение: где Или |