Free and bound charges. Polarization of matter

Free charges

are charges that, under the influence of field forces, can move freely in a substance; their movement is not limited by intramolecular forces.

Under bound charges

It is customary to understand electrical charges that are part of a substance and are held in certain positions by intramolecular forces. Such charges are “associated” with a given substance and are inseparable from it. The sum of positive bound charges is equal to the sum of negative bound charges.

If any dielectric body is placed in an electric field, it becomes polarized.

Under polarization

understand the ordered change in the arrangement of bound charges in a body caused by an electric field. This change in arrangement results in the negative bound charges in the body moving towards a higher potential and the positive bound charges moving towards a lower potential. The charges will shift so much that the forces of the electric field on the bound charges will be balanced by the intramolecular forces. As a result of polarization, bound charges appear to be exposed on the surface of the substance.

Polarization vector

The electric moment of two charges of equal magnitude and opposite sign, located at a distance l

(dipoles) is called the product
ql
.
This is a vector quantity directed from charge -q
to charge
+q
(Fig. 11.6,
a
).

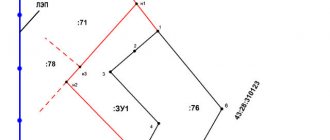
Rice. 11.6. On the issue of polarization of matter: a

) – electric dipole,
b
) – electric moment of the sum of dipoles,
c
) – location of bound charges in the dielectric.

In a polarized substance, molecules are electrically dipoles. Under the influence of an external electric field, dipoles tend to orient themselves in space in such a way that their electric moment is directed parallel to the electric field strength vector. Of practical interest is the electric moment of not one molecule, not one pair of charges, but the sum of dipoles located in a unit volume of a substance.

The electric moment of the sum of dipoles located in a unit volume of a substance is called the polarization vector and is denoted by the letter

. (11.12)

For most dielectrics P

to
the electric field strength
E. The proportionality coefficient between them is usually denoted by k
and is called electrical susceptibility

. (11.13)

All dielectrics with respect to the processes occurring in them during polarization can be divided into 2 groups.

The first group includes dielectrics, the molecules of which are electrically neutral in the absence of an external electric field, i.e. in them the centers of action of positive and negative charges coincide. Such dielectrics include hydrogen, nitrogen, paraffin, mica, etc.

Polarization in dielectrics of the first group consists in the fact that, under the influence of an external electric field, the center of action of the positive charge of the molecule will shift along the external field, and the center of action of negative charges will shift against the field. As a result, the molecule becomes a dipole. This displacement of the charges of the molecule is proportional to the strength of the external field. The displacement is counteracted by intramolecular forces.

The second group of dielectrics includes dielectrics, the molecules of which, in the absence of an external electric field, represent dipoles. In other words, the centers of action of the positive and negative charges of these molecules in the absence of an external electric field do not coincide (polar molecules). As a dielectric with polar molecules, hydrogen chloride, for example, can be mentioned.

Due to thermal motion, the dipoles are arranged randomly, so that in the absence of an external electric field, their electric fields cancel each other out. Polarization in dielectrics of the second group consists in the fact that polar molecules tend to rotate in such a way that their electric moment is directed along the external electric field.

Surface charge density

The formula for the electrostatic field potential in a dielectric φ will be written as:

φ = φ 0 + φ ' ( 1 ) with φ 0 being the field potential created by free charges, with φ ' being the field potential created by bound charges.

φ 0 = ∫ ρ d VR + ∫ σ d SR ( 2 ) , ρ is the volume density of free charges, σ is their surface density. Determination of the field potential of bound charges:

φ ' = ∫ P → R → R 3 d V ( 3 ) , where P → serves as the polarization vector.

We can conclude that from (1) and (3) we get:

φ = φ 0 + ∫ P → R → R 3 ( 4 ) .

When using the Ostrogradsky-Gauss theorem with some vector analysis formulas, we have a completely different form of equation (4):

φ = φ 0 + ∫ ρ s υ R d V + ∫ σ s υ R d V = ∫ ρ s υ + ρ R d V + ∫ σ s υ + σ R d V (5),

where ρ s υ is denoted as the average volume density of bound charges, and σ s υ is the average surface plane of bound charges. From equation (5) it can be seen that in the presence of a dielectric, the electric field coincides with the field created by free charges plus the field created by bound charges.

Density of bound charges

If P → = const, then the average density of bound charges is zero. This suggests that charges of the same sign do not accumulate in the dielectric. A surface bound density charge is concentrated at the boundary between a polarized dielectric and a vacuum or metal:

σ s υ = ± P n, - div P → = ρ s υ (6) with P n being the normal component of the polarization vector of the dielectric at its boundary with vacuum.

Function φ of the form (7) will be a solution to the equation:

∇ 2 φ = - 4 π ( ρ + ρ s υ ) ( 7 ) .

When E → = — ∇ φ → div E → = — ∇ 2 φ ( 8 ) and ( 6 ) we obtain:

div E → = 4 π ρ – 4 π div P → ( 9 ) .

div E → + 4 π P → = 4 π ρ ( 10 ) .

Expression (10) is called the basic differential equation of the electrostatic field in any arbitrary medium.

To obtain a complete system of electrostatic equations, you need to use formula (10) with a definition connecting the electric field strength vectors with the polarization vectors.

The dependence P → E → will be represented as:

P i = ε 0 ∑ j χ ij E j + ε 0 ∑ j , k χ ijk E j E k + . . . (11), where i, j serve to number the components along the axes of the Cartesian coordinate system (i = x, y, z; j = x, y, z), χ ij is the dielectric susceptibility tensor.

If there is an external electric field, the substance becomes a source of the field, which means the field changes.

What are free and bound charges

When we consider dielectrics in electrostatic fields, it is necessary to distinguish between two types of electric charges: free and bound.

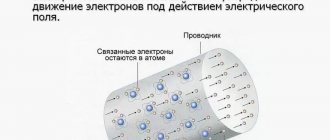
Free charges should be considered charges that can move over significant distances under the influence of a field, such as electrons in conductors, ions in gases, and charges brought from outside onto the surface of dielectrics that violate their (dielectrics) neutrality. Charges that are part of generally neutral dielectric molecules, as well as ions that are fixed in the crystal lattices of solid dielectrics near equilibrium positions, are called bound charges.

The potential of the electrostatic field in the dielectric ($varphi $) is equal to:

where $_0$ is the potential of the field created by free charges, $'$ is the potential of the field created by bound charges. At the same time, we know that:

where $ho$ is the volume density of free charges, $sigma$ is the surface density of free charges. The field potential of bound charges is defined as:

where $overrightarrow

$ is the polarization vector.

From equations (1) and (3) it follows that:

If you use the Ostrogradsky-Gauss theorem and some vector analysis formulas, it is not difficult to obtain a different form of equation (4), namely:

where $< ho >_$ is the average volumetric density of bound charges, $_ is the average surface density $ of bound charges. From equation (5) it is clear that the electric field in the presence of a dielectric coincides with the field that is created by free charges plus the field that is created by bound charges.

Free and bound charges. Polarization of matter

Free charges

are charges that, under the influence of field forces, can move freely in a substance; their movement is not limited by intramolecular forces.

Under bound charges

If any dielectric body is placed in an electric field, it becomes polarized.

Under polarization

Polarization vector

The electric moment of two charges of equal magnitude and opposite sign, located at a distance l

(dipoles) is called the product
ql
.
This is a vector quantity directed from charge -q
to charge
+q
(Fig. 11.6,
a
).

Rice. 11.6. On the issue of polarization of matter: a

) – electric dipole,
b
) – electric moment of the sum of dipoles,
c
) – location of bound charges in the dielectric.

The electric moment of the sum of dipoles located in a unit volume of a substance is called the polarization vector and is denoted by the letter

. (11.12)

For most dielectrics P

to
the electric field strength
E. The proportionality coefficient between them is usually denoted by k
and is called electrical susceptibility

. (11.13)

All dielectrics with respect to the processes occurring in them during polarization can be divided into 2 groups.

Density of bound charges

At $overrightarrow

=const$ (which means uniform polarization of the dielectric), the average density of bound charges is zero, which means that in this case there is no accumulation of charges of the same sign in the dielectric. A surface bound density charge is concentrated at the boundary between a polarized dielectric and a vacuum or metal:

where $P_n$ is the normal component of the polarization vector of the dielectric at its boundary with vacuum.

The function $varphi$ of the form (7) is a solution to the equation:

[overrightarrow=- abla varphi o divoverrightarrow=-< abla >^2varphi (8)]

and taking into account (6), we can write that:

[divoverrightarrow=4pi ho -4pi divoverrightarrow

(9)]

[divoverrightarrow<(E>+4pi overrightarrow

)=4pi ho left(10 ight).]

Equation (10) is the basic differential equation of the electrostatic field in any arbitrary medium.

In order to obtain a complete system of electrostatic equations to equation (10), it is necessary to add an expression connecting the electric field strength vectors and the polarization vector.

Dependency $overrightarrow

(overrightarrow)$ is generally presented as:

where the indices $i,j$ number the components along the axes of the Cartesian coordinate system $(i=x, y,z; j=x, y,z.)$, $_$ is the dielectric susceptibility tensor.

So, in the presence of an external electric field, the substance itself becomes a source of the field, therefore, the field changes.

Try asking your teachers for help

Assignment: There is a flat capacitor, the space between the plates of which is filled with a homogeneous, isotropic dielectric with dielectric susceptibility $varkappa$. There is a surface charge on the plates of the capacitor, its density is equal to $sigma.$ What is the strength of the resulting field in the capacitor?

If there is a vacuum between the capacitor plates, then the field strength created by the charged plates is equal to:

where $_0=8, 85cdot <10>^<-12>frac<Ф><m>. $—electric constant.

$+q, -q$ are charges on the capacitor plates.

$overrightarrow>$ is the field strength created by the capacitor plates.

$-q', +q'$ are charges of the dielectric.

$overrightarrow'$ is the field strength that is created as a result of polarization of the dielectric.

As the dielectric becomes polarized, the field strength decreases. Since we consider the dielectric to be homogeneous, the field that is created in a flat capacitor can also be considered homogeneous, we conclude that the polarization of the dielectric is uniform, that is, there are no volume bound charges ($< ho >_=0$). We have only surface charges whose density ($_$):

Knowing the relationship between field strength and polarization vector for an isotropic dielectric:

where $E$ is the projection of the intensity onto the outer normal to the dielectric surface. The field strength is directed from the positively charged plate of the capacitor to the negative one. Therefore, from (1.4) it follows that the surface density of the bound charge at the boundary with a positively charged plate has a minus sign, and at the boundary with a negative plate it has a plus sign. We find that the field strength in the dielectric between the capacitor plates is equal to the field strength in vacuum between the same plates, but with a surface charge density equal to:

On this basis, we write that the field strength in the capacitor in the presence of a dielectric is equal to:

Let us express from (1.6) the required tension:

Ask a question to the experts and get an answer within 15 minutes!

Free and bound charges in dielectrics. Polar and non-polar molecules. Types of dielectrics

When considering an electrostatic field, if there are dielectrics in it, it is necessary to distinguish between two types of electric charges: free and bound . By free charges we will understand, firstly, all electric charges that, under the influence of an electric field, can move over macroscopic distances (electrons in metals and vacuum, ions in gases and electrolytes, etc.), and, secondly, charges applied externally to the surface of dielectrics and violating their neutrality). The charges that are part of neutral dielectric molecules, as well as ions fixed in solid dielectrics near certain equilibrium positions, we will call bound charges.

Non-polar dielectrics (neutral) - consist of non-polar molecules in which the centers of gravity of positive and negative charges coincide. Therefore, non-polar molecules do not have an electric moment and their electric moment p = q • l = 0

. Examples of practically non-polar dielectrics used as electrical insulating materials are hydrocarbons, petroleum electrical insulating oils, polyethylene, polystyrene, etc.

Polar dielectrics (dipole) - consist of polar molecules that have an electric moment. In such molecules, due to their asymmetric structure, the centers of mass of positive and negative charges do not coincide. When replacing some of the hydrogen atoms in non-polar polymers with other atoms or non-hydrocarbon radicals, polar substances are obtained. When determining the polarity of a substance using a chemical formula, the spatial structure of the molecules should be taken into account. Polar dielectrics include phenol-formaldehyde and epoxy resins, organosilicon compounds, chlorinated hydrocarbons, etc.

Dielectrics

These are substances that, under normal conditions, practically do not conduct electric current; their resistivity is several times greater than that of metals.
According to the concepts of classical physics, in dielectrics, unlike conductors, there are no free charge carriers that could create a conduction current under the influence of an electric field. All gases are dielectrics; some liquids (distilled water, oils, benzene); solids (glass, porcelain, mica). The terms “dielectric” and “dielectric constant” were introduced into science in 1837 by M. Faraday. Dielectrics, like any substance, consist of atoms and molecules. In general, molecules are neutral, however, they interact with the electric field. For example, in the case when the symmetry of a molecule is different from spherical, it can be represented as an electric dipole
.
Electric dipole moment of a molecule
, where
q
is the total charge of nuclei or electrons;
l is a vector representing the arm of the equivalent dipole. Molecules that have an electric dipole moment are called polar. The polar dielectric is water; the following substances: CO; N2O; S2O; NH; HCl also contains polar molecules. In the volume of a substance, the dipole moments of molecules are distributed in different directions in a chaotic manner, so that their sum is zero. Molecules in which the positions of the equivalent positive and equivalent negative charge coincide and, therefore, the dipole moment of each molecule is zero () are called non-polar
. Substances such as are composed of non-polar molecules. If a dielectric is introduced into an electric field, then this field and the dielectric itself undergo significant changes.